3 X 36
stanleys
Sep 12, 2025 · 5 min read
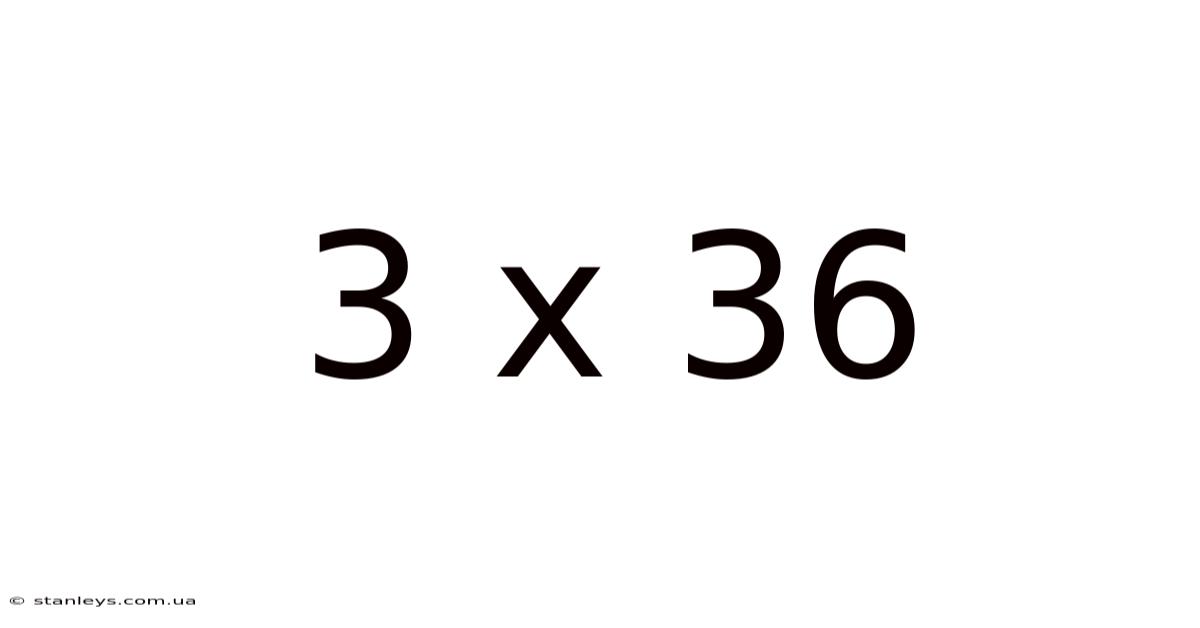
Table of Contents
Decoding 3 x 36: Unveiling the Mysteries of Multiplication and Beyond
The seemingly simple equation, 3 x 36, serves as a gateway to understanding a vast landscape of mathematical concepts. While the answer, 108, might appear straightforward at first glance, a deeper dive reveals intriguing connections to number theory, geometry, and even the world around us. This article explores the multifaceted nature of 3 x 36, examining its fundamental arithmetic, exploring its properties within number systems, and uncovering its surprising applications in various fields.
Understanding the Fundamentals: Multiplication and its Properties
At its core, 3 x 36 represents multiplication, a fundamental arithmetic operation. It signifies the repeated addition of 3, thirty-six times, or vice-versa. This basic understanding forms the bedrock for more complex mathematical explorations.
-
Commutative Property: Multiplication is commutative, meaning the order of the numbers doesn't affect the outcome. Therefore, 3 x 36 is equal to 36 x 3. This seemingly simple property has profound implications in algebraic manipulation and problem-solving.
-
Associative Property: The associative property allows us to group numbers differently without changing the result. For example, if we were multiplying 3 x 36 x 2, we could calculate (3 x 36) x 2 or 3 x (36 x 2) and obtain the same answer.
-
Distributive Property: The distributive property connects multiplication and addition. It states that a(b + c) = ab + ac. This property is crucial for simplifying expressions and solving equations. For instance, we can break down 3 x 36 as 3 x (30 + 6) = (3 x 30) + (3 x 6) = 90 + 18 = 108.
Exploring Number Systems: Beyond Base 10
Our typical understanding of numbers is rooted in the base-10 system (decimal system). However, exploring 3 x 36 in different number systems reveals intriguing insights into mathematical structures.
-
Binary System (Base 2): In the binary system, only 0 and 1 are used. Converting 3 and 36 to binary, we get 11 and 100100 respectively. Multiplying these binary numbers requires a different approach, involving binary addition and carries, ultimately resulting in the binary equivalent of 108.
-
Hexadecimal System (Base 16): The hexadecimal system uses digits 0-9 and letters A-F (representing 10-15). Converting 3 and 36 to hexadecimal gives 3 and 24 respectively. The multiplication process in hexadecimal is similar to decimal but involves carrying over when the result exceeds 15.
-
Other Bases: Exploring 3 x 36 in other bases, such as base 8 (octal) or base 12 (duodecimal), further emphasizes the flexibility and generality of mathematical operations. The underlying principles remain consistent across different number systems, although the representation and computational methods may vary.
The Number 108: A Deeper Dive into its Significance
The result of 3 x 36, 108, is a number rich in symbolic and mathematical significance across various cultures and disciplines.
-
Spiritual Significance: In many spiritual traditions, 108 holds profound symbolic meaning. It's often associated with sacred practices, representing the number of beads in a mala (prayer beads) used in meditation. It's also connected to various spiritual concepts and cycles.
-
Mathematical Properties: 108 is a highly composite number, meaning it has many divisors. It's also a spherical number, representing the number of vertices in a truncated icosahedron.
-
Geometric Significance: The number 108 appears in various geometric contexts. For instance, it’s related to the angles and proportions found within certain geometric shapes and constructions.
Applications in Real-World Scenarios
While seemingly abstract, the concepts related to 3 x 36 and its result, 108, have practical applications across various fields.
-
Measurement and Calculation: Imagine a scenario involving calculating the area of a rectangular plot of land measuring 3 meters by 36 meters. The multiplication 3 x 36 directly gives the area in square meters.
-
Inventory Management: In a warehouse containing 36 boxes with 3 items in each box, the total number of items can be easily determined using 3 x 36.
-
Financial Calculations: Financial calculations often involve multiplying quantities. For example, if an item costs $3 and you purchase 36 of them, the total cost is 3 x 36 = $108.
Expanding the Horizons: Further Mathematical Explorations
The simple equation 3 x 36 opens doors to a wealth of mathematical concepts that extend far beyond basic arithmetic.
-
Prime Factorization: Breaking down 3 and 36 into their prime factors (3 = 3 and 36 = 2² x 3²) allows us to understand the fundamental building blocks of these numbers. This process is crucial in number theory and cryptography.
-
Modular Arithmetic: Modular arithmetic involves working with remainders after division. Exploring 3 x 36 modulo various numbers unveils fascinating patterns and relationships.
-
Algebra and Equations: The concepts underlying 3 x 36 are fundamental to solving algebraic equations and inequalities.
Frequently Asked Questions (FAQ)
Q: What is the simplest way to calculate 3 x 36?
A: The simplest approach is to use the distributive property: 3 x (30 + 6) = (3 x 30) + (3 x 6) = 90 + 18 = 108. Alternatively, you can use traditional multiplication methods.
Q: What are some real-world examples where 3 x 36 might be used?
A: Examples include calculating areas, determining total quantities of items, computing costs, and various other counting and measurement tasks.
Q: Why is the number 108 considered significant in certain cultures?
A: 108 holds symbolic meaning in numerous spiritual traditions, often representing cycles, completeness, and spiritual practices.
Q: Can 3 x 36 be represented in other number systems?
A: Yes, 3 x 36 can be represented and calculated in binary, hexadecimal, and other number systems. The principles remain the same, but the representation and computational methods differ.
Conclusion: Beyond the Calculation
The seemingly simple calculation 3 x 36 unveils a wealth of mathematical concepts and connections. From fundamental arithmetic operations and the properties of numbers to their representation in different number systems and their applications in various fields, this exploration highlights the multifaceted nature of mathematics. The number 108, the result of this seemingly simple equation, further demonstrates the rich tapestry of mathematical relationships and their cultural significance. By delving deeper into these concepts, we gain a richer understanding not only of mathematics itself, but also its relevance to the world around us. The journey from a simple multiplication problem to a broader exploration of mathematical principles underscores the beauty and interconnectedness of mathematics.
Latest Posts
Latest Posts
-
25 Of 5000
Sep 12, 2025
-
96km To Miles
Sep 12, 2025
-
5 8 X 2
Sep 12, 2025
-
1 5 X 9
Sep 12, 2025
-
15 Of 280
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 X 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.