5.8 X 2
stanleys
Sep 12, 2025 · 6 min read
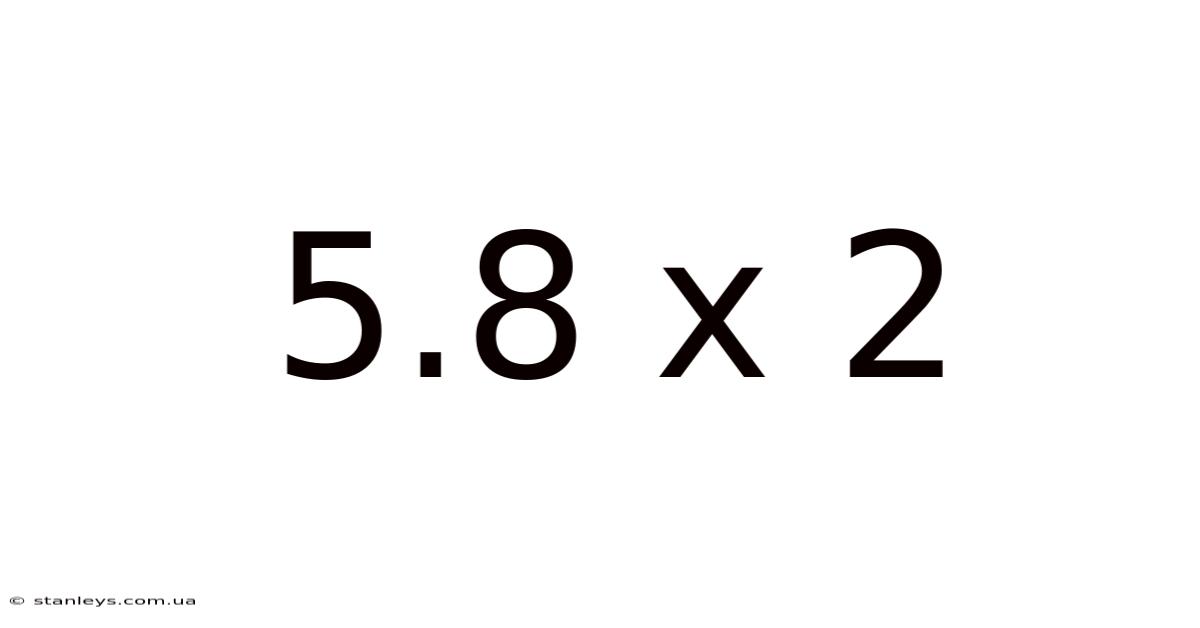
Table of Contents
Decoding 5.8 x 2: Exploring the Mathematical and Practical Applications of Multiplication
This article delves into the seemingly simple mathematical operation of 5.8 x 2, exploring its various applications beyond basic arithmetic. We'll unpack the calculation itself, examine its practical uses in everyday life, and delve into the broader mathematical concepts it embodies. Understanding this seemingly simple equation opens doors to a wider appreciation of mathematics and its pervasive influence in our world.
Understanding the Basics: Calculating 5.8 x 2
The core of this exploration begins with the fundamental calculation: 5.8 multiplied by 2. This can be approached in several ways:
-
Traditional Multiplication: We can perform the multiplication directly, treating 5.8 as 5 and 0.8 separately. 2 multiplied by 8 tenths is 16 tenths, or 1.6. 2 multiplied by 5 is 10. Adding these results (10 + 1.6) gives us the answer: 11.6.
-
Distributive Property: This method leverages the distributive property of multiplication over addition. We can rewrite 5.8 as (5 + 0.8). Then, the equation becomes 2 x (5 + 0.8) = (2 x 5) + (2 x 0.8) = 10 + 1.6 = 11.6.
-
Using Fractions: Expressing 5.8 as a fraction (58/10), the calculation becomes (58/10) x 2 = 116/10 = 11.6. This method highlights the relationship between decimals and fractions.
Regardless of the method chosen, the result remains constant: 5.8 multiplied by 2 equals 11.6. This simple calculation forms the foundation for understanding more complex mathematical problems.
Real-World Applications: Where 5.8 x 2 Appears
While seemingly straightforward, the calculation 5.8 x 2 frequently appears in diverse real-world scenarios. Let's explore some examples:
-
Shopping: Imagine buying two items priced at $5.80 each. The total cost is directly calculated as 5.8 x 2 = $11.60. This simple multiplication is integral to daily budgeting and financial planning.
-
Measurement: If you're working with lengths, areas, or volumes, the calculation might emerge. For instance, if a rectangular piece of land measures 5.8 meters in width and you need to double that width, the calculation yields a new width of 11.6 meters. Similarly, if a container holds 5.8 liters of liquid and you have two identical containers, the total capacity is 11.6 liters.
-
Recipe Scaling: Cooking often involves scaling recipes up or down. If a recipe calls for 5.8 ounces of an ingredient and you need to double the recipe, you'll need 11.6 ounces. This precise calculation ensures accurate proportions and consistent results.
-
Fuel Consumption: Suppose your car consumes 5.8 gallons of fuel per 100 miles, and you plan a 200-mile trip. A rough estimate of your fuel needs would involve this calculation: 5.8 gallons/100 miles x 200 miles ≈ 11.6 gallons. This illustrates the application in fuel efficiency calculations.
-
Scientific Experiments: In scientific research, particularly in areas dealing with measurements and data analysis, multiplying quantities by a factor of two is common. This simple calculation can be part of more complex calculations or data manipulations.
These are just a few examples. The simplicity of 5.8 x 2 belies its frequent appearance in diverse situations, highlighting the practical relevance of basic arithmetic in our daily lives.
Expanding the Concept: Beyond Simple Multiplication
While we've focused on the calculation 5.8 x 2, the underlying mathematical principles extend far beyond this single example. Let's explore some broader concepts:
-
Multiplication as Repeated Addition: At its core, multiplication is repeated addition. 5.8 x 2 is equivalent to 5.8 + 5.8. This fundamental understanding helps in visualizing the operation and grasping its meaning.
-
The Commutative Property: The commutative property of multiplication states that the order of the numbers doesn't change the result. 5.8 x 2 is the same as 2 x 5.8 = 11.6. This property simplifies calculations and enhances understanding.
-
The Associative Property: The associative property allows for regrouping numbers in multiplication without affecting the outcome. For instance, if we had (5.8 x 2) x 3, we could calculate either (5.8 x 2) first or (2 x 3) first, achieving the same result.
-
Decimal Arithmetic: This calculation highlights the importance of understanding decimal arithmetic. Mastering decimal multiplication is crucial for numerous mathematical applications.
-
Significance of Place Value: The calculation implicitly relies on understanding place value in the decimal system. The '5' represents 5 units, while the '8' represents 8 tenths. Maintaining the correct place value during calculations is crucial for accuracy.
Understanding these broader mathematical concepts enhances our ability to solve more complex problems and develop a deeper appreciation for the interconnectedness of mathematical ideas.
Practical Tips for Calculation and Application
-
Use a Calculator: For quick and accurate results, especially in scenarios demanding precision (like financial calculations), using a calculator is highly recommended.
-
Estimation: Before performing precise calculations, estimating the answer helps in verifying the reasonableness of the result. In this case, 5.8 is close to 6, so 6 x 2 = 12, suggesting that 11.6 is a plausible result.
-
Break Down Complex Problems: Larger, more complex problems can often be broken down into smaller, more manageable steps involving calculations like 5.8 x 2. This simplifies the process and reduces the chance of errors.
-
Practice: Consistent practice is key to mastering multiplication and other fundamental mathematical operations. Regular practice builds confidence and improves accuracy.
Frequently Asked Questions (FAQ)
-
Q: What is the best way to calculate 5.8 x 2?
- A: Any of the methods discussed (traditional multiplication, distributive property, or using fractions) will yield the correct answer (11.6). The best method depends on individual preference and the context of the problem.
-
Q: Are there any potential errors when calculating 5.8 x 2?
- A: The most common error is misplacing the decimal point during the calculation. Carefully tracking the decimal point is crucial for accuracy.
-
Q: How does this calculation relate to other mathematical concepts?
- A: This simple calculation illustrates fundamental concepts such as repeated addition, the commutative and associative properties of multiplication, decimal arithmetic, and the significance of place value.
-
Q: Why is understanding this calculation important?
- A: Understanding this seemingly simple calculation is foundational for grasping more complex mathematical concepts and applying them to real-world situations. It enhances problem-solving skills and numerical fluency.
Conclusion: The Significance of Simplicity
The seemingly simple calculation of 5.8 x 2 serves as a powerful illustration of the practical applications of basic mathematics. From everyday shopping to complex scientific experiments, understanding this fundamental operation opens doors to a wider appreciation of mathematics and its pervasive influence in our lives. By mastering this basic calculation and understanding its underlying principles, we build a stronger foundation for tackling more complex mathematical challenges and enhancing our problem-solving abilities in various aspects of life. The simplicity of 5.8 x 2 belies its significance in the broader world of numbers and their practical applications. Embrace the power of this seemingly simple calculation, and you will unlock a deeper understanding of the mathematical world around you.
Latest Posts
Latest Posts
-
Mariana Trench Pictures
Sep 12, 2025
-
Red Dress Red
Sep 12, 2025
-
50 2kg In Stone
Sep 12, 2025
-
320 Km Miles
Sep 12, 2025
-
700 5
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 5.8 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.