3 X 24
stanleys
Sep 13, 2025 · 6 min read
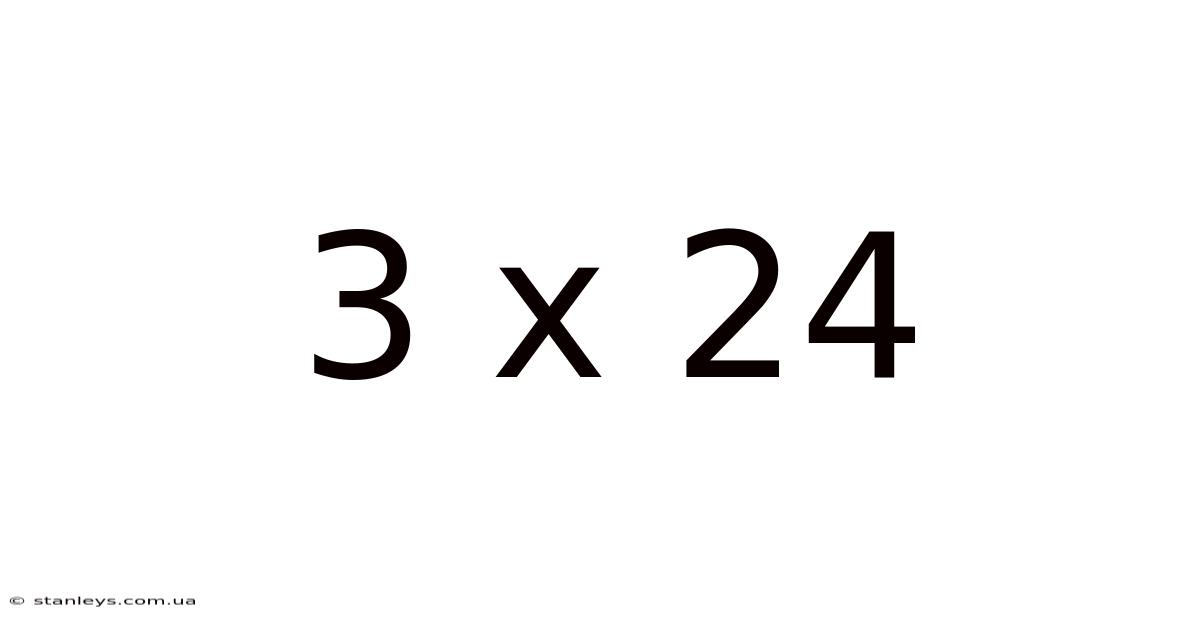
Table of Contents
Decoding 3 x 24: Exploring the Multifaceted Meaning and Applications of this Simple Equation
The seemingly simple equation, 3 x 24, often serves as a foundational element in various fields, from elementary arithmetic to complex calculations in advanced mathematics, physics, and even computer science. This article delves deep into the multifaceted interpretations and applications of 3 x 24, exploring its significance beyond its basic mathematical solution. We will examine its practical applications, its role in different learning contexts, and its potential for fostering deeper understanding of mathematical concepts. By the end, you'll appreciate the profound implications hidden within this unassuming equation.
I. The Fundamental Calculation: 3 x 24 = 72
At its core, 3 x 24 is a simple multiplication problem. The solution, 72, represents the total when three groups of 24 are combined. This fundamental calculation is the bedrock upon which many more complex mathematical operations are built. Understanding this basic multiplication is crucial for developing a solid foundation in mathematics. Mastering this simple equation helps students transition to more complex calculations involving larger numbers and different mathematical concepts.
- Method 1: Traditional Multiplication: This involves multiplying 3 by each digit of 24 separately and then adding the results. (3 x 4 = 12, 3 x 20 = 60, 12 + 60 = 72).
- Method 2: Distributive Property: This method involves breaking down 24 into smaller, easier-to-manage numbers. For instance, 24 can be broken down into 20 + 4. Then, 3 x (20 + 4) = (3 x 20) + (3 x 4) = 60 + 12 = 72. This approach strengthens understanding of fundamental mathematical properties.
- Method 3: Repeated Addition: This involves adding 24 three times: 24 + 24 + 24 = 72. This is a visual and intuitive method, especially beneficial for younger learners.
II. Practical Applications of 3 x 24 and the Number 72
The number 72, the product of 3 x 24, appears in various practical contexts:
- Time Measurement: 72 is directly related to time. There are 72 hours in three days. This connection makes it easy for students to visualize and grasp the concept of multiplication in a real-world scenario.
- Geometry and Measurement: 72 could represent areas, volumes, or angles in various geometric problems. For instance, a rectangle with dimensions 8 x 9 has an area of 72 square units. The number 72 also appears in various geometric constructions and calculations.
- Everyday Calculations: Imagine needing to calculate the total cost of three items costing $24 each. The equation 3 x 24 provides a quick and efficient solution. This highlights the equation's practical value in daily life.
- Data Analysis: In data analysis, the number 72 could represent a data point, a total count, or a result of a calculation. Understanding its origin through the equation 3 x 24 provides context and meaning.
III. Expanding the Concept: Variations and Extensions
The equation 3 x 24 offers opportunities to explore related mathematical concepts:
- Factors and Multiples: Understanding the factors of 72 (1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72) and its multiples broadens understanding of number theory. This provides a bridge to more advanced topics like prime factorization and greatest common divisors.
- Fractions and Decimals: The equation can be used to demonstrate fractions and decimals. For example, 3/4 of 72 can be calculated as (3/4) x 72 = 54. Similarly, decimal representations of fractions involving 72 can be explored.
- Algebraic Expressions: The equation can be adapted into algebraic expressions. For example, 3x = 72 can be solved for x, demonstrating the connection between multiplication and algebraic equations. This builds a foundational understanding for solving more complex algebraic problems.
- Ratio and Proportion: The concept of ratio and proportion can be explored using 3 x 24. For example, if 3 items cost $72, what is the cost of 6 items? This type of problem helps students understand proportional relationships.
IV. Pedagogical Approaches to Teaching 3 x 24
Effective teaching of 3 x 24 requires varied pedagogical approaches catering to different learning styles:
- Visual Aids: Using manipulatives like counters or blocks to represent the three groups of 24 provides a visual representation of multiplication. This concrete approach is especially effective for younger learners.
- Real-World Examples: Connecting the equation to real-world scenarios, like calculating the total cost of items or time spent on activities, makes the concept more relevant and engaging.
- Games and Activities: Incorporating games and interactive activities makes learning fun and encourages active participation. Examples include multiplication bingo or online math games.
- Differentiated Instruction: Teachers should cater to diverse learning styles and abilities. This may involve providing extra support for struggling learners or offering more challenging activities for advanced students.
V. The Number 72 in Different Cultural and Historical Contexts
The number 72 holds significance in various cultural and historical contexts:
- Numerology: In numerology, 72 is often associated with spiritual growth, manifestation, and abundance. Understanding this connection can help provide a wider perspective on the number's significance.
- Ancient Civilizations: The number 72 appears in various ancient civilizations' mathematical systems and architectural designs. Exploring these historical instances provides a rich context for the number's enduring presence.
- Music and Art: The number 72 might appear in musical compositions or artistic creations, highlighting its presence beyond pure mathematical applications.
VI. Advanced Applications: Connecting 3 x 24 to Higher-Level Mathematics
The seemingly simple 3 x 24 equation can serve as a gateway to more complex mathematical concepts:
- Modular Arithmetic: Exploring the remainder when 72 is divided by different numbers introduces modular arithmetic, a fundamental concept in number theory and cryptography.
- Calculus: While not directly involved, the understanding of multiplication and its properties is crucial for understanding concepts in calculus, such as limits and derivatives.
- Linear Algebra: The concept of scaling a vector (multiplying a vector by a scalar) is analogous to multiplication, highlighting the connection between elementary arithmetic and linear algebra.
VII. Frequently Asked Questions (FAQ)
Q1: What are some common mistakes students make when calculating 3 x 24?
A1: Common mistakes include errors in carrying over numbers during traditional multiplication, incorrect application of the distributive property, and miscounting during repeated addition.
Q2: How can I make learning 3 x 24 more engaging for students?
A2: Use visual aids, real-world examples, games, and differentiated instruction to cater to diverse learning styles. Incorporate technology and interactive learning tools.
Q3: What are some alternative ways to calculate 3 x 24 besides the standard methods?
A3: You can use mental math techniques, the lattice method, or even use a calculator (although this should be used sparingly to encourage understanding of the underlying processes).
Q4: Are there any real-world situations besides those mentioned where 3 x 24 is relevant?
A4: Many! Consider calculating the total number of items in three boxes containing 24 items each, or the total distance traveled over three days, with 24 km covered each day. The possibilities are endless.
VIII. Conclusion: The Unfolding Significance of 3 x 24
The seemingly simple equation, 3 x 24 = 72, unlocks a wealth of mathematical concepts and practical applications. By exploring its various interpretations and extensions, we see that this fundamental equation is not just a calculation but a gateway to deeper understanding in numerous fields. Its significance lies not just in its solution but in the learning journey it facilitates. From mastering basic multiplication to understanding more complex mathematical concepts, 3 x 24 serves as a stepping stone in a student's mathematical development, highlighting the power of seemingly simple equations to unlock a world of knowledge and understanding. This profound understanding, built from a foundation of simple calculations like 3 x 24, is crucial for fostering a lifelong love for mathematics and its applications.
Latest Posts
Latest Posts
-
85 Of 20
Sep 13, 2025
-
Useable Or Usable
Sep 13, 2025
-
53cm In Inches
Sep 13, 2025
-
95 X 2
Sep 13, 2025
-
58 9kg In Stones
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 X 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.