3 X 19
stanleys
Sep 13, 2025 · 5 min read
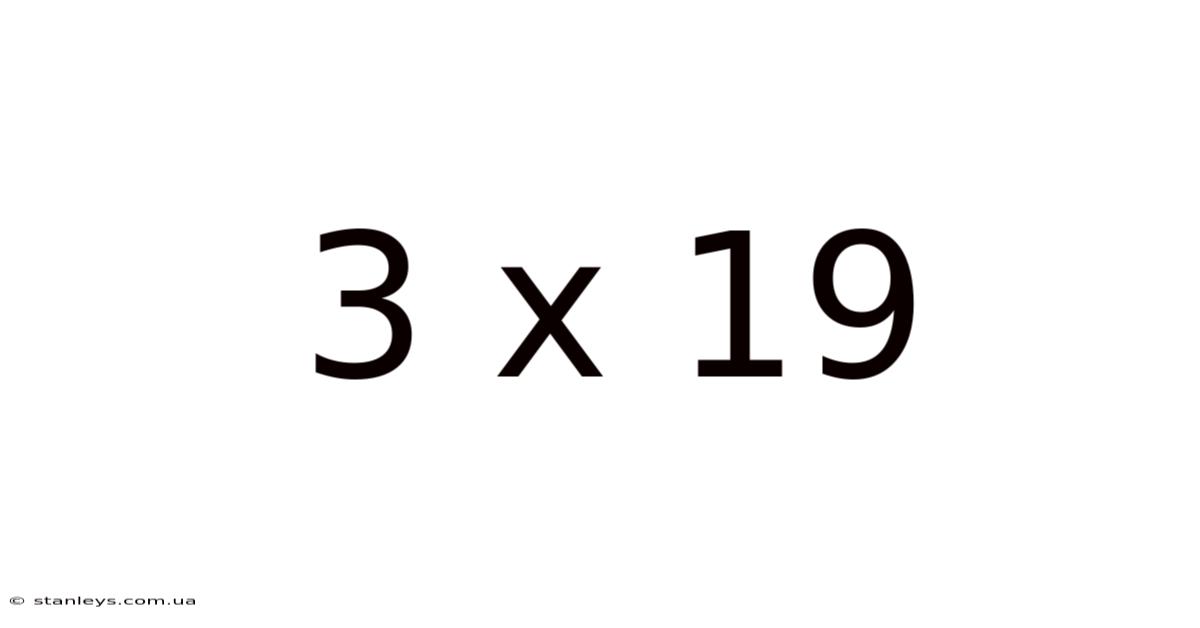
Table of Contents
Unpacking 3 x 19: A Deep Dive into Multiplication, Factors, and More
This seemingly simple equation, 3 x 19, opens a door to a wealth of mathematical concepts. It's more than just a basic multiplication problem; it's a springboard for exploring factors, multiples, prime numbers, and even the broader world of arithmetic operations. This article delves into the intricacies of 3 x 19, providing a comprehensive understanding accessible to learners of all levels, from elementary school to advanced studies. We'll cover the basics, explore the underlying mathematical principles, and even delve into some real-world applications.
Understanding the Fundamentals: Multiplication and its Properties
At its core, 3 x 19 represents multiplication – a fundamental arithmetic operation. Multiplication is essentially repeated addition. In this case, 3 x 19 means adding the number 19 three times: 19 + 19 + 19 = 57. This simple understanding lays the groundwork for more complex mathematical operations.
Multiplication possesses several key properties:
- Commutative Property: The order of numbers doesn't change the result. 3 x 19 is the same as 19 x 3. Both equal 57.
- Associative Property: When multiplying more than two numbers, the grouping doesn't matter. For example, (3 x 2) x 9.5 is the same as 3 x (2 x 9.5). This is relevant when dealing with more complex equations involving 3 and 19.
- Distributive Property: This allows us to break down multiplication into smaller, manageable parts. For instance, 3 x (20 - 1) = (3 x 20) - (3 x 1) = 60 - 3 = 57. This property is invaluable in mental math and more complex algebraic manipulations.
- Identity Property: Multiplying any number by 1 results in the original number. This might seem trivial, but it's crucial in understanding the multiplicative identity.
Factors and Multiples: Exploring the Relationships
The numbers 3 and 19 are factors of 57. Factors are numbers that divide evenly into a larger number without leaving a remainder. We can find the factors of 57 by systematically checking which numbers divide into it evenly: 1, 3, 19, and 57. This simple exercise illustrates the concept of factorization, a cornerstone of many higher-level mathematical concepts.
Conversely, 57 is a multiple of both 3 and 19. Multiples are the products of a number and any integer. For example, other multiples of 3 are 6, 9, 12, and so on. Similarly, multiples of 19 include 38, 57, 76, and so forth. Understanding the relationship between factors and multiples provides a fundamental understanding of number theory.
Prime Numbers: The Building Blocks of Arithmetic
The number 19 is a prime number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means that 19 can only be divided evenly by 1 and 19. Prime numbers are considered the "building blocks" of all other numbers because all composite numbers (non-prime numbers greater than 1) can be expressed as a unique product of prime numbers. This fundamental principle is known as the Fundamental Theorem of Arithmetic.
In the equation 3 x 19 = 57, we see the interplay between a prime number (19) and a smaller prime factor (3). Understanding prime numbers helps us understand the fundamental structure of numbers and is critical in cryptography and other advanced fields.
Practical Applications: Real-World Examples of 3 x 19
While 3 x 19 might seem like a purely abstract mathematical concept, it has numerous practical applications:
- Everyday Calculations: Imagine you're buying three items that cost $19 each. The total cost would be 3 x $19 = $57. This demonstrates the practical application of multiplication in everyday scenarios.
- Measurement and Conversion: If you're working with measurements, understanding multiplication is essential. For instance, calculating the area of a rectangle with dimensions of 3 units and 19 units would directly involve this calculation.
- Data Analysis and Statistics: In data analysis, you may encounter scenarios requiring multiplying frequencies or probabilities. The equation 3 x 19 could represent a calculation within a larger statistical analysis.
- Computer Science and Programming: At the core of computer programming lies arithmetic operations. The simple equation is a building block for more complex algorithms.
Beyond the Basics: Expanding Our Understanding
The equation 3 x 19 = 57 is a starting point for exploring a wide range of mathematical concepts. Here are some areas for further exploration:
- Modular Arithmetic: Exploring the remainder when 57 is divided by different numbers. This concept has applications in cryptography and computer science.
- Algebraic Manipulation: Using the equation to illustrate algebraic concepts like solving for unknowns.
- Geometry: Exploring how the equation might relate to geometric problems, such as calculating the area of a rectangle.
- Number Theory: Delving into the properties of 3, 19, and 57 within the broader context of number theory.
Frequently Asked Questions (FAQ)
Q: What are the factors of 57?
A: The factors of 57 are 1, 3, 19, and 57.
Q: Is 57 a prime number?
A: No, 57 is a composite number because it has more than two factors.
Q: How can I use 3 x 19 in real-life situations?
A: You can use it to calculate costs, areas, or in various data analysis scenarios. See the "Practical Applications" section above for more examples.
Q: What are some other ways to calculate 3 x 19?
A: You can use repeated addition (19 + 19 + 19), the distributive property (3 x (20-1)), or mental math techniques.
Q: What is the significance of prime numbers like 19?
A: Prime numbers are fundamental building blocks of all numbers, and they play crucial roles in number theory and cryptography.
Conclusion: The Richness of a Simple Equation
The simple equation 3 x 19 = 57 offers a gateway to a vast landscape of mathematical concepts. From the fundamental properties of multiplication to the intricacies of prime numbers and their applications, this seemingly simple equation reveals the depth and interconnectedness of mathematics. By exploring this example, we not only solidify our understanding of basic arithmetic but also gain a glimpse into the more complex and fascinating world of higher mathematics and its real-world implications. This exploration should inspire further investigation and a deeper appreciation for the power and elegance of numbers. The journey of understanding 3 x 19 is a journey into the heart of mathematics itself.
Latest Posts
Latest Posts
-
44 Of 781
Sep 13, 2025
-
9 20 Of 540
Sep 13, 2025
-
1 7km In Miles
Sep 13, 2025
-
165lbs En Kg
Sep 13, 2025
-
45k In Miles
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 X 19 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.