3/5 Of 30
stanleys
Sep 10, 2025 · 6 min read
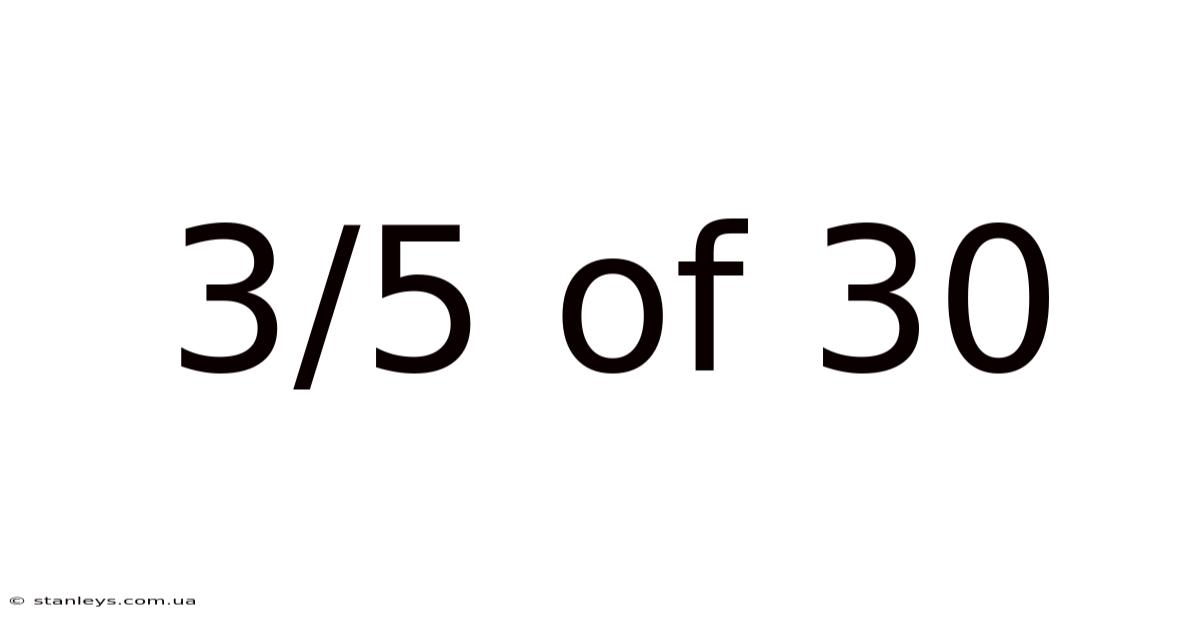
Table of Contents
Decoding 3/5 of 30: A Deep Dive into Fractions and Their Applications
Finding "3/5 of 30" might seem like a simple arithmetic problem, suitable only for elementary school. However, this seemingly straightforward calculation opens the door to a much broader understanding of fractions, their practical applications, and their importance in various fields. This article will not only solve the problem but will also explore the underlying concepts, provide different solution methods, and delve into real-world examples where this type of calculation is crucial.
Understanding Fractions: The Building Blocks
Before tackling "3/5 of 30," let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. In our example, 3/5, the numerator is 3 and the denominator is 5. This means we are considering 3 parts out of a total of 5 equal parts.
Solving 3/5 of 30: Methods and Approaches
There are several ways to calculate 3/5 of 30. Let's explore the most common methods:
Method 1: Direct Multiplication
The most straightforward method involves converting the fraction to a decimal and then multiplying. To convert 3/5 to a decimal, we divide the numerator (3) by the denominator (5): 3 ÷ 5 = 0.6. Now, we multiply this decimal by 30: 0.6 * 30 = 18. Therefore, 3/5 of 30 is 18.
Method 2: Fraction Multiplication
Another approach utilizes direct fraction multiplication. We can express 30 as a fraction by placing it over 1 (30/1). Then, we multiply the two fractions:
(3/5) * (30/1) = (3 * 30) / (5 * 1) = 90 / 5
Now, we simplify the resulting fraction by dividing the numerator (90) by the denominator (5): 90 ÷ 5 = 18. Again, we arrive at the answer: 18.
Method 3: Finding a Fifth, Then Multiplying by Three
This method involves breaking down the problem into smaller, more manageable steps. First, we find one-fifth (1/5) of 30 by dividing 30 by 5: 30 ÷ 5 = 6. Since we want three-fifths (3/5), we multiply this result by 3: 6 * 3 = 18. This method is particularly helpful for visualizing the fraction and understanding the concept of parts of a whole.
Beyond the Calculation: Real-World Applications
While finding "3/5 of 30" might seem abstract, this type of calculation has numerous practical applications in everyday life and various professional fields:
-
Shopping and Discounts: Imagine a store offering a 3/5 discount on a $30 item. Using our calculation, we know the discount amount is $18, leaving a final price of $12.
-
Recipe Scaling: If a recipe calls for 3/5 of a cup of flour and you want to triple the recipe, you'd need to calculate 3/5 of 3 cups (or 3 * 3/5 of a cup).
-
Financial Calculations: Fractions are fundamental in finance, used in calculating interest rates, loan payments, and stock market analyses. Understanding fractional parts is crucial for making informed financial decisions.
-
Construction and Engineering: Engineers and architects frequently use fractions in blueprint calculations, material estimations, and structural designs. Accuracy in these calculations is paramount for safety and efficiency.
-
Data Analysis: In statistics and data analysis, fractions are used to represent proportions and percentages. Understanding fractional relationships helps in interpreting data and drawing meaningful conclusions.
-
Probability and Statistics: Probability calculations often involve fractions. For example, if there's a 3/5 chance of rain, this means there are 3 favorable outcomes out of a total of 5 possible outcomes.
Understanding Percentages and Their Relationship to Fractions
The problem of finding "3/5 of 30" can also be approached using percentages. We know that 3/5 is equivalent to 60% (because (3/5) * 100% = 60%). Therefore, finding 3/5 of 30 is the same as finding 60% of 30. This can be calculated as: (60/100) * 30 = 18. This demonstrates the close relationship between fractions and percentages, offering alternative calculation methods.
Expanding the Concept: Working with More Complex Fractions
While our example uses a relatively simple fraction, the principles apply to more complex scenarios. For instance, consider calculating 7/12 of 48. The same methods can be applied:
-
Direct Multiplication: 7/12 = 0.5833 (approximately), 0.5833 * 48 ≈ 28
-
Fraction Multiplication: (7/12) * (48/1) = 336/12 = 28
-
Breaking it down: 1/12 of 48 is 4, so 7/12 of 48 is 7 * 4 = 28.
Frequently Asked Questions (FAQ)
-
Q: What if the fraction and the whole number don't simplify easily? A: Even if the numbers don't simplify easily, the same methods apply. Use a calculator if necessary for the decimal conversion or the final division step. The fundamental principle remains the same.
-
Q: Can I use this concept with larger numbers? A: Absolutely! The principles discussed here apply to any combination of fractions and whole numbers. The calculations might become more complex, but the underlying methodology remains consistent.
-
Q: Why are fractions important to learn? A: Fractions are a fundamental building block in mathematics. Understanding fractions is essential for mastering more advanced concepts like algebra, calculus, and beyond. Their practical applications are widespread, impacting various aspects of our daily lives.
-
Q: What if I need to find a fraction of a fraction? A: This involves multiplying two fractions together. Remember to multiply numerators and denominators separately, then simplify the resulting fraction. For example, (1/2) * (2/3) = (12)/(23) = 2/6 = 1/3.
-
Q: How do I convert a decimal to a fraction? A: To convert a decimal to a fraction, write the decimal as the numerator over a denominator of a power of 10. For example, 0.75 becomes 75/100. Then, simplify the fraction by finding the greatest common divisor of the numerator and denominator. 75/100 simplifies to 3/4.
Conclusion: Mastering Fractions for a Brighter Future
Calculating 3/5 of 30, while simple in itself, provides a valuable opportunity to explore the world of fractions. This seemingly basic arithmetic exercise lays the groundwork for understanding more complex mathematical concepts and their widespread applications in real-world scenarios. Mastering fractions is not just about solving equations; it's about developing problem-solving skills, critical thinking, and a deeper understanding of the quantitative world around us. From budgeting to construction to scientific research, a solid grasp of fractions is an invaluable asset. So, the next time you encounter a fraction problem, remember that it's not just about finding the answer – it's about building a strong foundation for future learning and success.
Latest Posts
Latest Posts
-
15 Of 35 00
Sep 10, 2025
-
Wrenches That Ratchet
Sep 10, 2025
-
100 Divided 12
Sep 10, 2025
-
23 X 8
Sep 10, 2025
-
Antonym For Truculent
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3/5 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.