3/4 Of 32
stanleys
Sep 14, 2025 · 5 min read
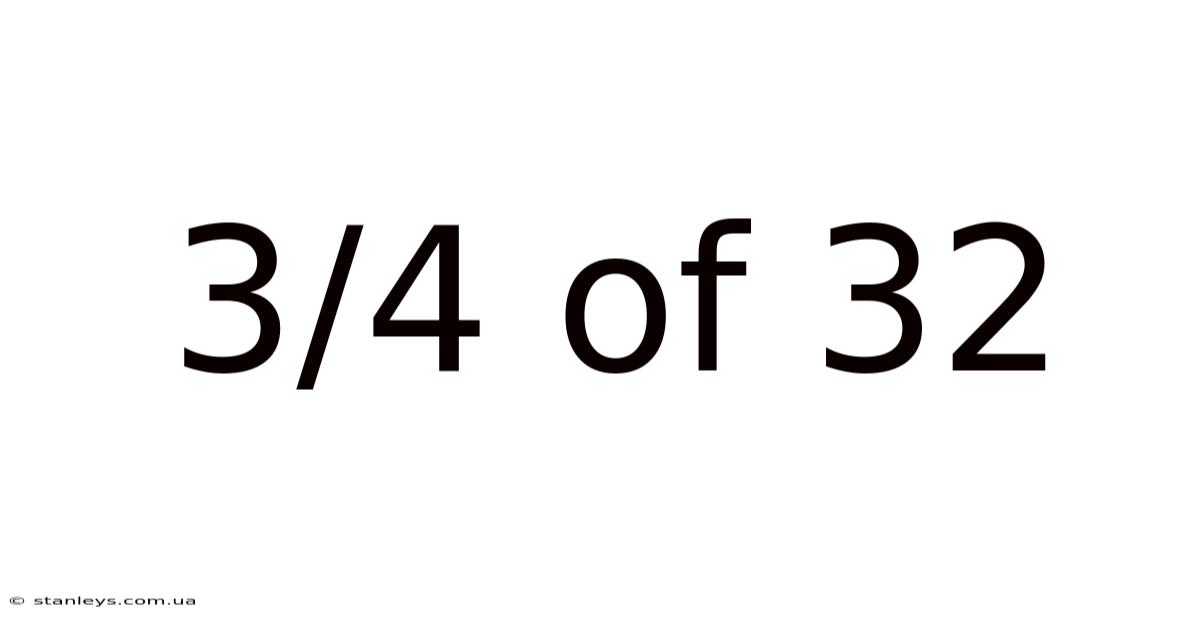
Table of Contents
Decoding 3/4 of 32: A Deep Dive into Fractions and Their Applications
Finding 3/4 of 32 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a world of mathematical concepts with far-reaching applications in everyday life, from calculating discounts to understanding proportions in scientific experiments. This article will not only show you how to solve 3/4 of 32 but will also delve into the underlying principles, explore different approaches to solving the problem, and examine its relevance in various contexts.
Understanding Fractions: The Building Blocks
Before tackling 3/4 of 32, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 3/4 means we have 3 parts out of a total of 4 equal parts.
Method 1: Converting the Fraction to a Decimal
One straightforward way to find 3/4 of 32 is to convert the fraction 3/4 into a decimal. To do this, we simply divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Now, we multiply this decimal by 32:
0.75 x 32 = 24
Therefore, 3/4 of 32 is 24.
This method is particularly useful when using a calculator, making it quick and efficient for larger numbers.
Method 2: Finding the Unit Fraction and Multiplying
Another approach involves understanding the concept of a unit fraction. A unit fraction is a fraction where the numerator is 1 (e.g., 1/2, 1/4, 1/10). First, we find 1/4 of 32 by dividing 32 by 4:
32 ÷ 4 = 8
Since 1/4 of 32 is 8, we can find 3/4 of 32 by multiplying this result by 3:
8 x 3 = 24
Again, we arrive at the answer: 3/4 of 32 is 24. This method emphasizes the proportional relationship between fractions and offers a clear visual representation of the problem.
Method 3: Visual Representation with a Diagram
For a more intuitive understanding, especially for visual learners, we can use a diagram. Imagine a rectangle divided into four equal parts. Each part represents 1/4 of the whole. If the total value of the rectangle is 32, then each part represents:
32 ÷ 4 = 8
Since we want to find 3/4, we shade three of the four parts. The total value of the shaded area is:
8 x 3 = 24
The diagram visually confirms that 3/4 of 32 is 24. This method is particularly helpful for grasping the concept of fractions and their representation.
The Importance of Understanding Proportions
The calculation of 3/4 of 32 is fundamentally about understanding proportions. A proportion is a statement that two ratios are equal. In this case, we can set up a proportion as follows:
3/4 = x/32
Where 'x' represents the unknown value (3/4 of 32). To solve for 'x', we can cross-multiply:
4x = 3 x 32
4x = 96
x = 96 ÷ 4
x = 24
This method reinforces the concept of equivalent fractions and their application in solving proportional problems. It's a powerful technique applicable in a wide range of scenarios, from scaling recipes to determining the size of a model based on a blueprint.
Real-World Applications: From Shopping to Science
Understanding fractions and their applications isn't just about passing math tests; it's crucial for navigating everyday life. Consider these examples:
-
Shopping: A store offers a 25% discount on an item priced at $32. Since 25% is equivalent to 1/4, the discount amount is 1/4 of $32, which is $8. The final price after the discount would be $32 - $8 = $24. This demonstrates the direct application of fraction calculations in saving money.
-
Cooking: A recipe calls for 3/4 cup of flour, but you want to double the recipe. You'll need 3/4 cup x 2 = 1.5 cups of flour. Understanding fractions allows for accurate scaling of recipes to accommodate different serving sizes.
-
Construction and Engineering: In construction and engineering, precise measurements and proportions are critical. Fractions are fundamental in calculating material quantities, determining angles, and ensuring structural integrity. Even seemingly small errors in fractional calculations can lead to significant problems.
-
Data Analysis: In statistics and data analysis, fractions and percentages are extensively used to represent proportions and probabilities. Understanding fractions is essential for interpreting data and drawing meaningful conclusions.
Frequently Asked Questions (FAQ)
Q: Can I solve this problem using percentages?
A: Absolutely! 3/4 is equivalent to 75%. To find 75% of 32, you can multiply 32 by 0.75 (which is the decimal representation of 75%), resulting in 24.
Q: Are there other methods to solve this problem?
A: Yes, while the methods described are common and straightforward, other advanced mathematical techniques, such as using ratios and proportions or applying algebraic equations, could also be employed.
Q: What if the fraction was more complex, such as 7/12 of 36?
A: The same principles apply. You can use any of the methods described (converting to decimals, finding the unit fraction, or using proportions) to solve the problem. The complexity increases, but the underlying concepts remain the same.
Q: Why is understanding fractions so important?
A: Fractions are fundamental to mathematics and have broad applications in various fields. Mastering fractions builds a solid foundation for more advanced mathematical concepts and problem-solving skills applicable in numerous real-world situations.
Conclusion: Mastering Fractions for a Brighter Future
Finding 3/4 of 32 might seem like a minor calculation, but it serves as a gateway to a deeper understanding of fractions, proportions, and their widespread applications. By mastering this seemingly simple problem, we unlock a powerful tool for tackling more complex mathematical challenges and enhancing our ability to analyze and solve problems in various aspects of life. From everyday shopping to intricate scientific calculations, the ability to work confidently with fractions is an invaluable skill that empowers us to navigate the world more effectively and efficiently. The seemingly simple act of calculating 3/4 of 32 is a testament to the power of fundamental mathematical concepts and their far-reaching impact on our lives.
Latest Posts
Latest Posts
-
Psi To Kilopascal
Sep 14, 2025
-
5000 3
Sep 14, 2025
-
72mm In Inches
Sep 14, 2025
-
Too Much Makeup
Sep 14, 2025
-
Painting Door Frames
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.