28 40 Simplified
stanleys
Sep 15, 2025 · 5 min read
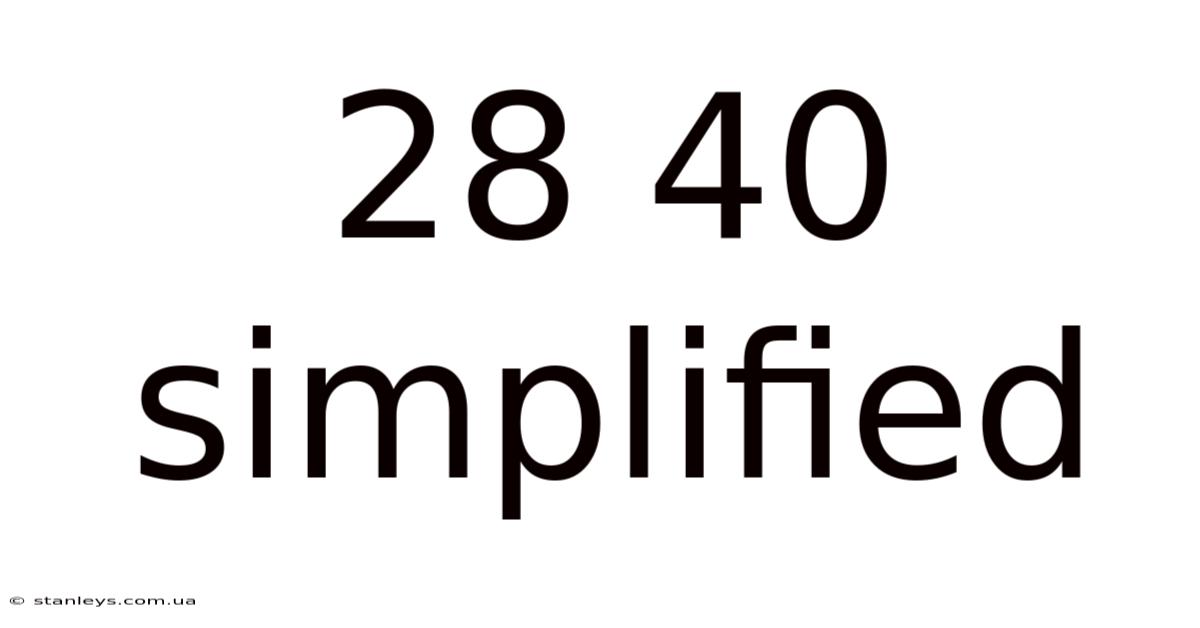
Table of Contents
Decoding the 28/40 Simplified: A Comprehensive Guide to Understanding and Mastering this Fraction
The fraction 28/40 might seem deceptively simple at first glance. However, understanding its simplification, its applications in various mathematical contexts, and its broader implications within the field of fractions provides a valuable foundation for stronger mathematical skills. This comprehensive guide will delve into the intricacies of 28/40, exploring its simplification process, real-world applications, and frequently asked questions, ultimately empowering you to confidently tackle similar fractional problems.
Introduction: Understanding Fractions and Simplification
Before diving into the specifics of 28/40, let's establish a fundamental understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
Simplification, also known as reducing a fraction, involves finding an equivalent fraction with a smaller numerator and denominator. This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD). Simplifying fractions makes them easier to understand and work with, and it's a crucial skill in various mathematical operations.
Step-by-Step Simplification of 28/40
The simplification of 28/40 involves identifying the GCD of 28 and 40. Here's a step-by-step approach:
-
Find the factors of 28: The factors of 28 are 1, 2, 4, 7, 14, and 28.
-
Find the factors of 40: The factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40.
-
Identify the common factors: Comparing the lists, we find that the common factors of 28 and 40 are 1, 2, and 4.
-
Determine the greatest common factor (GCD): The largest common factor is 4. This is the GCD of 28 and 40.
-
Simplify the fraction: Divide both the numerator (28) and the denominator (40) by the GCD (4):
28 ÷ 4 = 7 40 ÷ 4 = 10
Therefore, the simplified form of 28/40 is 7/10.
Alternative Methods for Finding the GCD
While listing factors is a straightforward method, especially for smaller numbers, other techniques can be more efficient for larger numbers. These include:
-
Prime factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
28 = 2² x 7 40 = 2³ x 5
The common prime factor is 2, and the lowest power is 2². Therefore, the GCD is 2² = 4.
-
Euclidean algorithm: This iterative method is particularly useful for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Real-World Applications of Fractions like 28/40
Fractions, including simplified fractions like 7/10, are ubiquitous in everyday life. Here are some examples:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. For example, a recipe might require 7/10 of a cup of sugar.
-
Measurement: Many measurements involve fractions, such as inches, centimeters, or parts of a liter.
-
Finance: Calculating percentages, discounts, and interest often involves working with fractions.
-
Probability and Statistics: Fractions are fundamental in expressing probabilities and statistical data. The probability of an event might be represented as 7/10, meaning there's a 70% chance of it occurring.
-
Geometry and Mensuration: Calculating areas, volumes, and other geometric properties often requires working with fractions.
-
Data Representation: Graphs and charts frequently use fractions to represent proportions and percentages of data.
Beyond Simplification: Operations with Fractions
Understanding fraction simplification is crucial for performing other operations with fractions, such as:
-
Addition and Subtraction: Before adding or subtracting fractions, you need to find a common denominator. This often involves simplifying fractions first to make the process easier.
-
Multiplication: Multiplying fractions involves multiplying the numerators together and the denominators together. Simplifying before multiplication can often simplify the result.
-
Division: Dividing fractions involves inverting the second fraction (the divisor) and then multiplying. Again, simplifying beforehand can make the calculation simpler.
Frequently Asked Questions (FAQ)
Q1: Is 7/10 the simplest form of 28/40?
A1: Yes, 7/10 is the simplest form of 28/40 because 7 and 10 share no common factors other than 1.
Q2: What if I made a mistake and didn't find the greatest common divisor?
A2: If you don't find the greatest common divisor in the first attempt, you can still simplify the fraction further by continuing to divide the numerator and denominator by their common factors until you reach the simplest form. However, using the GCD ensures that you reach the simplest form in one step.
Q3: Why is simplifying fractions important?
A3: Simplifying fractions makes them easier to understand and work with. It simplifies calculations, improves accuracy, and allows for easier comparisons between fractions. Simplified fractions are also essential for representing data clearly and concisely.
Q4: Are there any online tools or calculators that can simplify fractions?
A4: Yes, many online calculators and tools can simplify fractions. These tools can be helpful for checking your work or for simplifying more complex fractions. However, understanding the underlying process is crucial for building your mathematical skills.
Q5: Can a fraction have a negative numerator or denominator?
A5: Yes, a fraction can have a negative numerator, a negative denominator, or both. A fraction with a negative numerator and a positive denominator, or a positive numerator and a negative denominator, will result in a negative value. A fraction with both a negative numerator and a negative denominator will result in a positive value.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Mastering the simplification of fractions like 28/40 is a fundamental step in developing a strong foundation in mathematics. This seemingly simple task underlies a broader understanding of fractions, their applications, and their role in more complex mathematical operations. By understanding the process, the various methods for finding the GCD, and the real-world implications of fractions, you'll be well-equipped to tackle more advanced mathematical concepts with confidence and efficiency. Remember, practice is key; the more you work with fractions, the more comfortable and proficient you'll become. So, grab a pencil and paper, and start practicing! You'll be surprised how quickly your understanding and skill improve.
Latest Posts
Latest Posts
-
54 1kg In Stone
Sep 15, 2025
-
2 X 60
Sep 15, 2025
-
57inches In Cm
Sep 15, 2025
-
Pascal To Mpa
Sep 15, 2025
-
2 X 3 12
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 28 40 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.