2 X 3/12
stanleys
Sep 15, 2025 · 5 min read
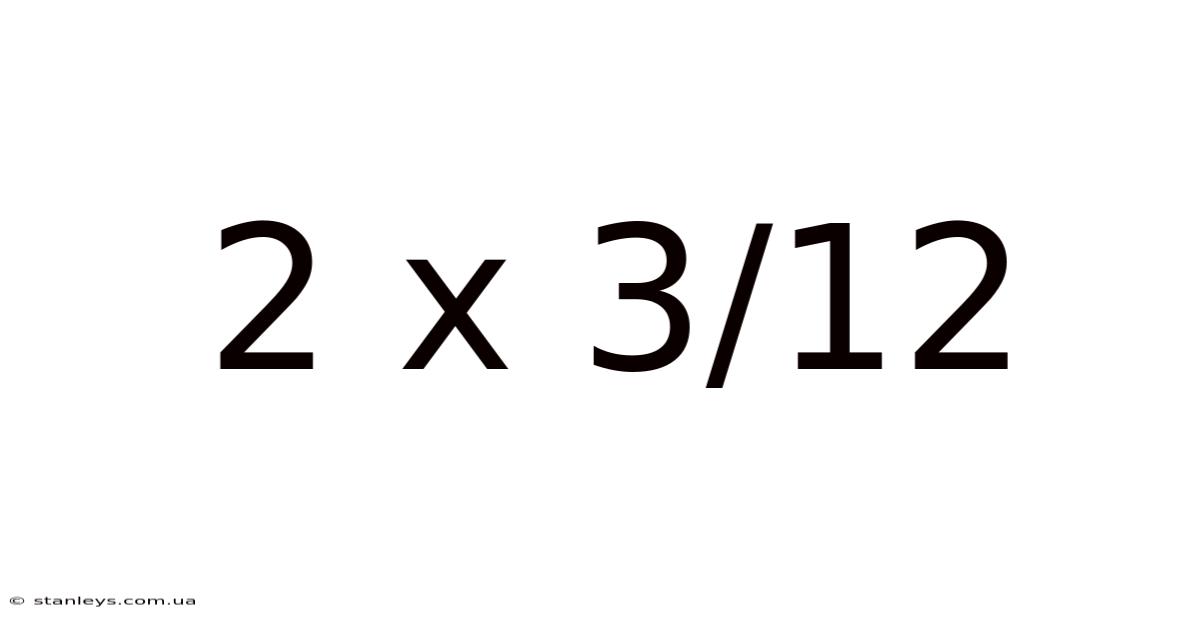
Table of Contents
Decoding 2 x 3/12: A Deep Dive into Fraction Multiplication
This article explores the seemingly simple mathematical expression "2 x 3/12," delving far beyond the immediate answer to uncover the underlying principles of fraction multiplication and its real-world applications. We'll break down the process step-by-step, examine the mathematical concepts involved, explore different approaches to solving the problem, and finally, discuss the broader implications of understanding fraction multiplication. This comprehensive guide is perfect for students struggling with fractions, teachers looking for engaging explanations, and anyone curious about the elegance and practicality of mathematics.
Understanding the Components: Whole Numbers and Fractions
Before tackling the multiplication, let's understand the components of our expression: 2 and 3/12.
-
2: This is a whole number, representing two complete units. Think of it as two apples, two cars, or two of anything.
-
3/12: This is a fraction. Fractions represent parts of a whole. The top number,
3, is the numerator, indicating how many parts we have. The bottom number,12, is the denominator, showing the total number of equal parts the whole is divided into. In this case, we have 3 parts out of a total of 12 equal parts.
Method 1: Simplifying Before Multiplying
One of the most efficient ways to solve 2 x 3/12 is by simplifying the fraction before performing the multiplication. This simplifies the calculation and makes it easier to grasp the concept.
Step 1: Simplify the Fraction
The fraction 3/12 can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 3 and 12 is 3. Dividing both the numerator and the denominator by 3, we get:
3 ÷ 3 / 12 ÷ 3 = 1/4
Now our expression becomes: 2 x 1/4
Step 2: Multiply the Whole Number and the Simplified Fraction
Multiplying a whole number by a fraction involves multiplying the whole number by the numerator and keeping the denominator the same:
2 x 1/4 = (2 x 1) / 4 = 2/4
Step 3: Simplify the Result (If Necessary)
The fraction 2/4 can be further simplified by dividing both the numerator and the denominator by their GCD, which is 2:
2 ÷ 2 / 4 ÷ 2 = 1/2
Therefore, 2 x 3/12 = 1/2
Method 2: Multiplying First, Then Simplifying
Alternatively, we can multiply the whole number by the fraction directly and then simplify the resulting fraction.
Step 1: Multiply the Whole Number and the Fraction
Multiply the whole number (2) by the numerator of the fraction (3):
2 x 3 = 6
Keep the denominator the same (12):
The result is 6/12
Step 2: Simplify the Result
Simplify the fraction 6/12 by finding the GCD of 6 and 12, which is 6:
6 ÷ 6 / 12 ÷ 6 = 1/2
Again, we arrive at the same answer: 2 x 3/12 = 1/2
Visualizing the Multiplication
Imagine you have two pizzas, each cut into 12 equal slices. The fraction 3/12 represents 3 slices of one pizza. The expression 2 x 3/12 means you have two pizzas, and you take 3 slices from each. That's a total of 6 slices (6/12). Simplifying 6/12, you get 1/2, representing half a pizza.
The Mathematical Principle Behind Fraction Multiplication
The core principle behind multiplying fractions (and whole numbers with fractions) is straightforward: multiply the numerators together and multiply the denominators together. This can be expressed as:
(a/b) x (c/d) = (a x c) / (b x d)
In our example, 2 can be written as 2/1. Therefore:
(2/1) x (3/12) = (2 x 3) / (1 x 12) = 6/12 = 1/2
This formula holds true for all fraction multiplications.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it has numerous real-world applications:
-
Cooking: If a recipe calls for 1/2 cup of flour and you want to double the recipe, you'll need to calculate 2 x 1/2 = 1 cup of flour.
-
Construction: Measuring and cutting materials often involves fractions. Determining the amount of wood needed for a project might require multiplying fractions to account for different lengths and widths.
-
Finance: Calculating interest, discounts, or portions of a budget frequently involves fraction multiplication.
-
Data Analysis: Working with percentages and proportions in data analysis relies heavily on the principles of fraction multiplication.
Addressing Common Mistakes and Misconceptions
-
Forgetting to simplify: Many students make the mistake of leaving their answer as an unsimplified fraction (e.g., 6/12 instead of 1/2). Always simplify your answer to its lowest terms.
-
Incorrect multiplication: Ensure you multiply the numerators together and the denominators together correctly. A simple arithmetic error can lead to an incorrect answer.
-
Confusing multiplication with addition or subtraction: Remember that multiplying fractions is different from adding or subtracting them. Different rules apply.
Frequently Asked Questions (FAQ)
-
Can I multiply the whole number by the denominator before simplifying? No, that would lead to an incorrect result. You should either simplify the fraction first or multiply the numerators and denominators separately and then simplify.
-
What if the fraction is an improper fraction (numerator > denominator)? The same rules apply. Multiply the numerators, multiply the denominators, and then simplify the resulting fraction. You might end up with a whole number or a mixed number.
-
How do I multiply mixed numbers? To multiply mixed numbers, first convert them to improper fractions, then follow the standard rules of fraction multiplication.
-
Why is simplifying important? Simplifying fractions makes the answer easier to understand and use in practical applications. It presents the answer in its most concise form.
Conclusion: Mastering Fraction Multiplication
Understanding and mastering fraction multiplication is crucial for success in mathematics and its countless real-world applications. By breaking down the problem into smaller steps, utilizing simplification techniques, and visualizing the process, the seemingly complex task becomes manageable and even enjoyable. The methods and explanations provided in this article offer a solid foundation for tackling more complex fraction problems and for appreciating the beauty and practicality of mathematical principles. Remember to practice regularly, apply the concepts to real-world scenarios, and don't hesitate to review the steps if needed. With consistent effort, you'll confidently navigate the world of fractions and their multiplications.
Latest Posts
Latest Posts
-
The Sleeping Giant
Sep 15, 2025
-
85grams To Oz
Sep 15, 2025
-
Intermittent Fire Alarm
Sep 15, 2025
-
98f To C
Sep 15, 2025
-
40 Times 8
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2 X 3/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.