25 Of 160
stanleys
Sep 13, 2025 · 5 min read
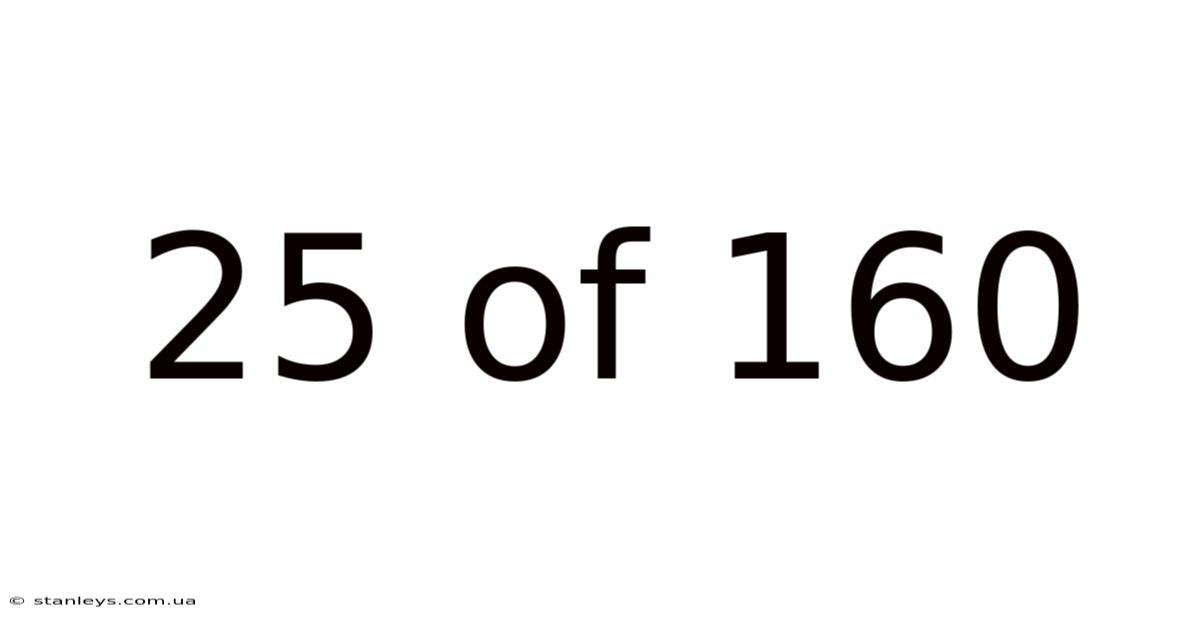
Table of Contents
Decoding the Mystery: Understanding the Fraction 25/160
The seemingly simple fraction 25/160 might appear intimidating at first glance, especially for those less comfortable with mathematical concepts. However, understanding this fraction opens the door to a deeper understanding of fraction simplification, decimal conversion, and their applications in various fields. This article will explore the fraction 25/160 comprehensively, guiding you through simplification, conversion, real-world applications, and answering frequently asked questions. We'll demystify this fraction, empowering you with the tools to tackle similar mathematical challenges with confidence.
Introduction: Why 25/160 Matters
The fraction 25/160 represents a part-to-whole relationship. It signifies 25 units out of a total of 160 units. While seemingly specific, this fraction exemplifies fundamental mathematical principles applicable across various contexts, from calculating proportions in recipes to understanding statistical data. Mastering the techniques used to simplify and interpret 25/160 directly translates to improved problem-solving skills in algebra, geometry, and even everyday life. Understanding its decimal equivalent also proves crucial in practical scenarios requiring precise measurements or percentages.
Step-by-Step Simplification of 25/160
Simplifying fractions is crucial for easier understanding and calculation. The goal is to reduce the fraction to its simplest form, where the numerator and denominator have no common factors other than 1. This process involves finding the greatest common divisor (GCD) of both the numerator (25) and the denominator (160).
Here's a step-by-step approach:
-
Find the factors of 25: The factors of 25 are 1, 5, and 25.
-
Find the factors of 160: The factors of 160 are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, and 160.
-
Identify the greatest common divisor (GCD): Comparing the factors of 25 and 160, we see that the largest common factor is 5.
-
Divide both the numerator and denominator by the GCD:
25 ÷ 5 = 5 160 ÷ 5 = 32
Therefore, the simplified form of 25/160 is 5/32. This simplified fraction is easier to work with and represents the same proportional relationship as the original fraction.
Converting 5/32 to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case, we divide 5 by 32:
5 ÷ 32 = 0.15625
Therefore, the decimal equivalent of 5/32 (and consequently 25/160) is 0.15625. This decimal representation is particularly useful when working with calculators, computers, or situations requiring numerical precision.
Real-World Applications of 25/160 and 5/32
The fraction 25/160, and its simplified form 5/32, finds applications in various real-world scenarios:
-
Percentage Calculations: To express 5/32 as a percentage, multiply the decimal equivalent (0.15625) by 100: 0.15625 * 100 = 15.625%. This could represent, for example, the percentage of students who achieved a particular score on a test.
-
Proportions and Ratios: Imagine a recipe calling for 25 grams of sugar in a total mixture of 160 grams. Simplifying the fraction to 5/32 provides a clearer understanding of the sugar-to-mixture ratio.
-
Measurement and Scaling: If you're working with a blueprint where a measurement is represented by 25 units on the drawing and 160 units in reality, simplifying the fraction allows for easier scaling calculations.
-
Probability: In probability calculations, 5/32 could represent the probability of a specific event occurring, giving a clearer understanding of the likelihood.
Further Exploration: Understanding Fraction Operations
While this article focuses on 25/160, understanding the principles behind its simplification and conversion allows you to tackle other fractions with confidence. Let's briefly touch upon some common fraction operations:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. If the denominators are different, find the least common multiple (LCM) and adjust the fractions accordingly.
-
Multiplication: Multiplying fractions is straightforward: multiply the numerators together and the denominators together. Simplify the resulting fraction if necessary.
-
Division: To divide fractions, invert the second fraction (reciprocal) and then multiply.
Mastering these operations is fundamental to advanced mathematical concepts and problem-solving.
Frequently Asked Questions (FAQs)
Q1: Is there more than one way to simplify 25/160?
A1: While there might be multiple steps involved, the end result of simplification will always be the same – 5/32. The GCD is unique for any given pair of numbers. You might choose to simplify in stages (e.g., dividing by 5, then by another common factor), but the final simplified fraction will remain the same.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand and work with. It provides a clearer representation of the ratio and facilitates calculations, especially in more complex problems involving multiple fractions. It also helps in comparing fractions more easily.
Q3: Can any fraction be simplified?
A3: Not all fractions can be simplified. If the numerator and denominator share no common factors other than 1, the fraction is already in its simplest form. For example, 7/11 is already simplified.
Q4: What if I get a repeating decimal when converting a fraction?
A4: Some fractions result in repeating decimals (e.g., 1/3 = 0.333...). This indicates that the decimal representation is infinite and non-terminating. In such cases, it’s often acceptable to round the decimal to a specific number of decimal places depending on the context and required level of accuracy.
Q5: Are there any online tools or calculators to help simplify fractions?
A5: Yes, numerous online tools and calculators are available to simplify fractions and perform other fraction operations. These tools can be helpful for verification or when dealing with larger, more complex fractions.
Conclusion: Embracing the Power of Fractions
Understanding fractions, even seemingly simple ones like 25/160, is a crucial building block in mathematics and numerous applications in daily life. By learning how to simplify fractions, convert them to decimals, and understand their real-world implications, you’ve equipped yourself with valuable problem-solving skills. Remember that the process of simplification isn't just about arriving at the answer; it’s about understanding the underlying mathematical principles and developing a strong foundation for more advanced mathematical concepts. The journey from 25/160 to 5/32 is a testament to the power of mathematical simplification and the elegance of reducing complexity to its core essence. Embrace the journey of learning, and you’ll find that the world of mathematics opens up in exciting and unexpected ways.
Latest Posts
Latest Posts
-
57 7kg In Stone
Sep 13, 2025
-
5 4 In Cm
Sep 13, 2025
-
57 4kg In Stones
Sep 13, 2025
-
200 15
Sep 13, 2025
-
Sodapop Patrick Curtis
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.