1/3 Of 90
stanleys
Sep 11, 2025 · 6 min read
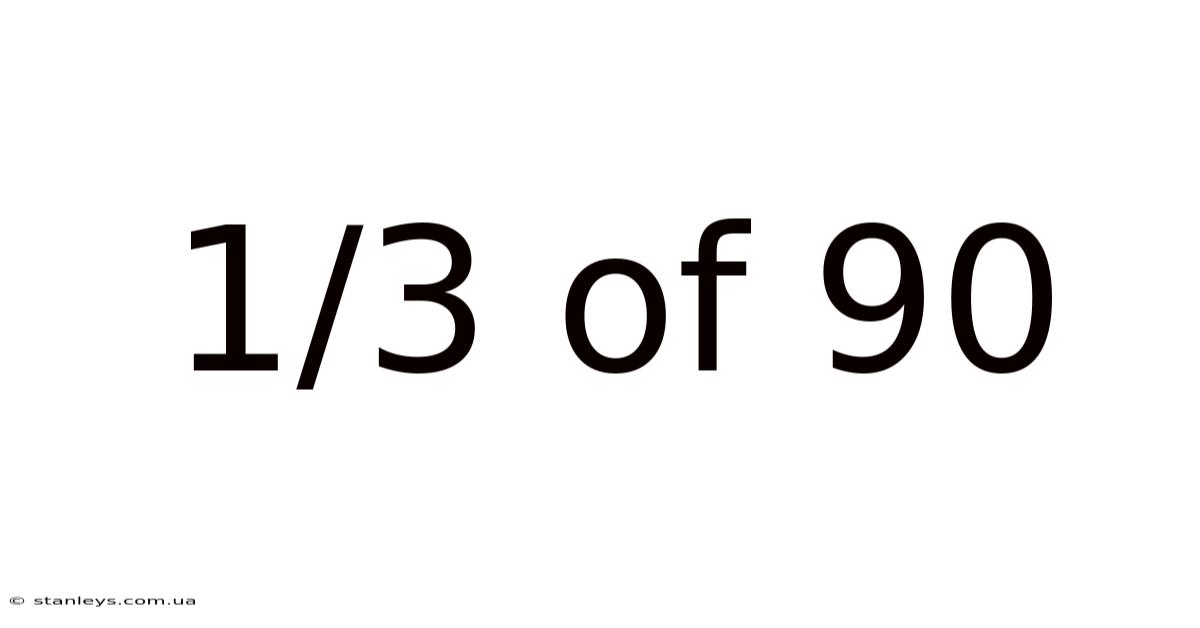
Table of Contents
Decoding 1/3 of 90: A Deep Dive into Fractions and Their Applications
Finding 1/3 of 90 might seem like a simple arithmetic problem, suitable only for elementary school. However, this seemingly straightforward calculation offers a gateway to understanding fundamental mathematical concepts with broad applications across various fields. This article will not only solve this problem but also explore the underlying principles of fractions, their practical uses, and even touch upon their historical significance. We’ll delve into different methods of solving the problem, exploring the why behind the calculations and showing how this basic concept builds a foundation for more complex mathematical operations. This comprehensive guide is perfect for anyone looking to refresh their understanding of fractions or delve deeper into the subject.
Understanding Fractions: A Foundation for Calculation
Before we tackle 1/3 of 90, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. In the fraction 1/3, 1 is the numerator and 3 is the denominator. This means we're considering one part out of a total of three equal parts.
Fractions are ubiquitous in daily life. From cooking (e.g., 1/2 cup of sugar) to measuring distances (e.g., 2/3 of a mile) and sharing resources (e.g., splitting a pizza equally among friends), fractions are essential for accurate representation and problem-solving. A strong understanding of fractions is crucial for further mathematical advancements, including algebra, calculus, and more.
Method 1: Direct Calculation – The Simplest Approach
The most straightforward way to calculate 1/3 of 90 is to multiply the fraction by the whole number. This involves multiplying the numerator (1) by 90 and then dividing the result by the denominator (3):
(1/3) * 90 = (1 * 90) / 3 = 90 / 3 = 30
Therefore, 1/3 of 90 is 30. This method highlights the core principle of finding a fraction of a number: multiplication by the numerator and division by the denominator.
Method 2: Dividing into Equal Parts – A Visual Approach
This method offers a more intuitive understanding of fractions. Imagine you have 90 objects, and you want to divide them into three equal groups. To do this, you simply perform the division:
90 / 3 = 30
Each group contains 30 objects. Since 1/3 represents one of these three equal groups, 1/3 of 90 is 30. This approach makes the concept of fractions more concrete, particularly helpful for visual learners. It reinforces the idea that the denominator dictates the number of equal parts, and the numerator selects how many of those parts we are considering.
Method 3: Using Decimal Equivalents – An Alternative Perspective
Fractions can also be expressed as decimals. The fraction 1/3 is equivalent to the repeating decimal 0.333... While this decimal representation is infinite, we can use a suitable approximation for practical purposes. Multiplying 90 by the decimal equivalent of 1/3 gives:
90 * 0.333... ≈ 29.999...
Rounding this result gives us 30. This method demonstrates the interchangeability between fractions and decimals, highlighting another facet of numerical representation. However, it’s important to acknowledge the limitations of using decimal approximations, especially when dealing with repeating decimals. The direct fraction calculation remains more accurate in this instance.
Expanding the Concept: Fractions Beyond the Basics
Understanding 1/3 of 90 is a stepping stone to mastering more complex fractional calculations. This includes:
-
Finding fractions of larger numbers: Applying the same principles, we can calculate 1/3 of any number, regardless of size. For instance, 1/3 of 270 would be (1/3) * 270 = 90.
-
Working with mixed numbers: Mixed numbers combine a whole number and a fraction (e.g., 2 1/3). To find a fraction of a mixed number, you would first convert it into an improper fraction (a fraction where the numerator is greater than the denominator), then proceed with the multiplication and division.
-
Adding, subtracting, multiplying, and dividing fractions: This is where the true power of fractional understanding comes into play. The ability to manipulate fractions through these operations is vital for solving a wide range of problems in mathematics and beyond.
-
Fractions in Algebra: Fractions form a critical component of algebraic expressions and equations. The ability to simplify, manipulate, and solve equations containing fractions is a cornerstone of advanced mathematics.
Real-World Applications of Fractions
The concept of fractions is not confined to the classroom; it has widespread practical applications in various fields:
-
Cooking and Baking: Recipes often require specific fractional amounts of ingredients (e.g., 2/3 cup of flour, 1/4 teaspoon of salt).
-
Construction and Engineering: Precise measurements are essential in construction and engineering projects. Fractions are crucial for accurate calculations of lengths, volumes, and angles.
-
Finance and Economics: Fractions are used extensively in finance, for example, when calculating percentages, interest rates, and shares of ownership.
-
Data Analysis and Statistics: Fractions are fundamental in representing proportions and probabilities in data analysis and statistical studies.
-
Science: Many scientific calculations and measurements involve the use of fractions, particularly in areas such as physics and chemistry.
Frequently Asked Questions (FAQs)
Q: Why is it important to learn about fractions?
A: Fractions are fundamental to mathematics and have countless real-world applications. A solid understanding of fractions is crucial for success in higher-level mathematics and various professional fields.
Q: What if the number isn't easily divisible by the denominator?
A: Even if the number isn't perfectly divisible by the denominator, the same principles apply. You'll simply end up with a fraction as the result. For example, 1/3 of 80 would be (1/3) * 80 = 80/3, which can be simplified to the mixed number 26 2/3.
Q: Are there other ways to represent 1/3 of 90?
A: Yes, you can represent it as a decimal (30.0), a percentage (33.33%), or even in ratio form (1:3 if you're considering the relationship between the part and the whole).
Q: How do I improve my understanding of fractions?
A: Practice is key! Work through various problems involving fractions, starting with simpler ones and gradually increasing the difficulty. Visual aids, like diagrams and real-world examples, can also be helpful.
Conclusion: The Enduring Significance of Fractions
Calculating 1/3 of 90, while seemingly simple, offers a profound glimpse into the world of fractions. This seemingly basic calculation showcases fundamental mathematical principles with far-reaching applications in various fields. From simple everyday tasks to complex scientific calculations, fractions are an indispensable tool for understanding and manipulating numerical quantities. Mastering the concept of fractions is not just about solving arithmetic problems; it's about developing a crucial skill that will serve you well throughout your academic and professional life. Continue to explore the world of fractions, and you’ll unlock a deeper understanding of the mathematical language that governs our world.
Latest Posts
Latest Posts
-
Hz To Radians Second
Sep 11, 2025
-
Chu Papi Munyanyo
Sep 11, 2025
-
Half Of 48
Sep 11, 2025
-
41kg In Lbs
Sep 11, 2025
-
125kg In Lbs
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.