25 Of 145
stanleys
Sep 16, 2025 · 5 min read
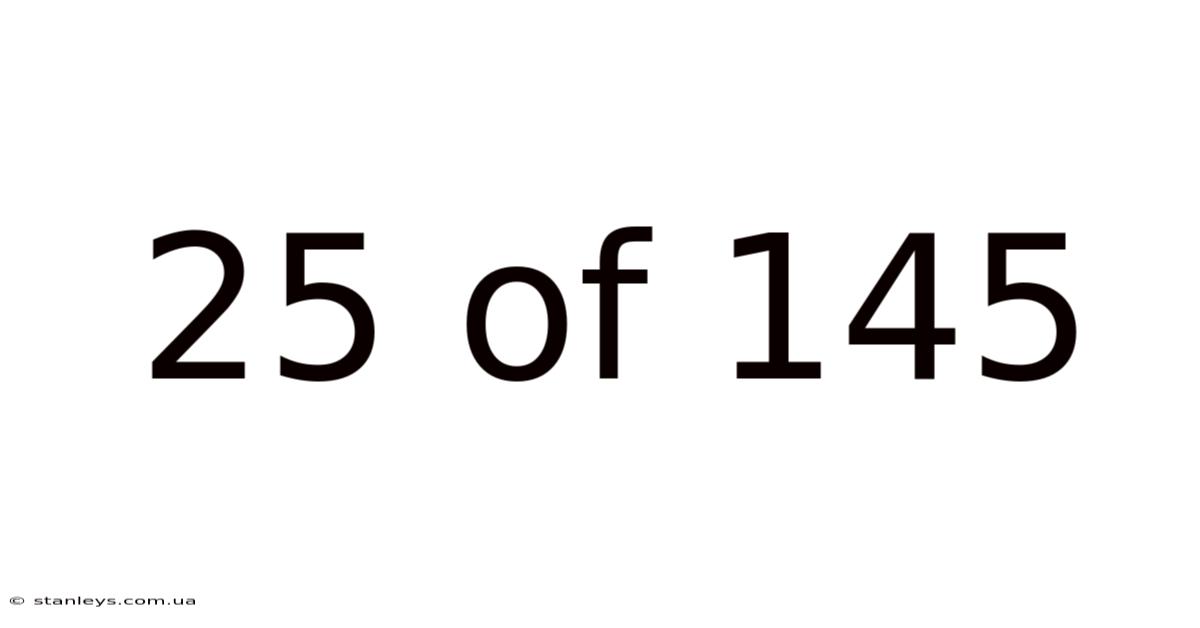
Table of Contents
Unveiling the Mystery: Understanding the Fraction 25/145
The seemingly simple fraction 25/145 might appear straightforward at first glance, but beneath its surface lies a world of mathematical concepts ripe for exploration. This article delves into the intricacies of this fraction, exploring its simplification, decimal representation, percentage equivalent, and real-world applications, aiming to provide a comprehensive understanding for students and anyone curious about the beauty of numbers. We will also examine related concepts and answer frequently asked questions about fractions in general.
Introduction: A Deeper Dive into 25/145
The fraction 25/145 represents a part-to-whole relationship, where 25 is the part and 145 is the whole. Understanding this fundamental relationship is key to mastering fractions. This article aims to demystify this specific fraction and provide a broader understanding of fractional concepts. We will navigate through the processes of simplification, conversion to decimal and percentage forms, and discuss the practical applications of such representations in various contexts. This exploration will enhance your understanding not just of 25/145, but also of the broader principles governing fractions.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into other representations, simplifying the fraction is crucial. This process involves finding the greatest common divisor (GCD) of the numerator (25) and the denominator (145). The GCD is the largest number that divides both 25 and 145 without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down both numbers into their prime factors:
- 25 = 5 x 5 = 5²
- 145 = 5 x 29
The only common prime factor is 5. Therefore, the GCD of 25 and 145 is 5.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
25 ÷ 5 / 145 ÷ 5 = 5/29
Therefore, the simplified form of 25/145 is 5/29. This simplified fraction is equivalent to the original fraction, representing the same part-to-whole relationship in its most concise form.
2. Converting to Decimal Representation
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. In this case, we divide 5 by 29:
5 ÷ 29 ≈ 0.1724
The decimal representation of 5/29 is approximately 0.1724. Note that this is an approximation because the decimal representation of 5/29 is a non-terminating decimal (it continues infinitely without repeating). We often round the decimal to a certain number of decimal places depending on the required level of precision.
3. Expressing as a Percentage
To express the fraction as a percentage, we multiply the decimal representation by 100:
0.1724 x 100 ≈ 17.24%
Therefore, 5/29 is approximately 17.24%. This percentage represents the proportion of the whole that the fraction represents.
4. Real-World Applications: Understanding Proportions
Fractions, like 25/145 and its simplified form 5/29, are incredibly useful in various real-world scenarios. Let's consider some examples:
-
Calculating Proportions: Imagine a class of 145 students, where 25 students scored above 90% on a test. The fraction 25/145 (simplified to 5/29) represents the proportion of students who scored above 90%. This allows for easy comparison with other classes or assessments.
-
Mixing Ingredients: In cooking or baking, recipes often call for fractional amounts of ingredients. Understanding fractions is essential to accurately measure and mix these ingredients. For instance, if a recipe requires 5/29 of a cup of flour, you would need to accurately measure this amount.
-
Financial Calculations: Fractions are fundamental in financial calculations, such as determining interest rates, calculating profits and losses, or representing parts of a share in a company.
-
Scientific Measurements: Scientific measurements often involve fractions, especially in areas like physics and chemistry, where precise measurements are critical.
-
Probability: In probability theory, fractions are used to express the likelihood of an event occurring. The fraction represents the ratio of favorable outcomes to the total number of possible outcomes.
5. Exploring Related Concepts: Fractions, Decimals, and Percentages
The interconnectedness of fractions, decimals, and percentages is crucial to understand. They are simply different ways to represent the same part-to-whole relationship.
-
Fractions: Represent a part-to-whole relationship using a numerator (top number) and a denominator (bottom number).
-
Decimals: Represent a part-to-whole relationship using a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
-
Percentages: Represent a part-to-whole relationship as a fraction of 100. They are often used to express proportions or rates.
Understanding how to convert between these three forms is a fundamental skill in mathematics.
6. Frequently Asked Questions (FAQs)
-
Q: What is the simplest form of 25/145?
-
A: The simplest form of 25/145 is 5/29.
-
Q: How do I convert a fraction to a decimal?
-
A: Divide the numerator by the denominator.
-
Q: How do I convert a fraction to a percentage?
-
A: Divide the numerator by the denominator, then multiply by 100.
-
Q: Are there any other methods to find the GCD besides prime factorization?
-
A: Yes, the Euclidean algorithm is another efficient method to find the GCD of two numbers.
-
Q: What if the decimal representation of a fraction is non-terminating and non-repeating?
-
A: This indicates an irrational number, which cannot be expressed as a simple fraction. We usually approximate such numbers to a certain number of decimal places.
-
Q: Why is simplifying fractions important?
-
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also presents the fraction in its most concise form.
7. Conclusion: Mastering Fractions – A Building Block of Mathematics
Understanding fractions like 25/145 is not just about manipulating numbers; it's about grasping the fundamental concept of representing parts of a whole. The ability to simplify, convert, and apply fractions to real-world situations is a crucial skill that extends far beyond the classroom. This comprehensive exploration of 25/145 has hopefully provided a solid foundation for understanding fractions, their various representations, and their widespread applications in various fields. Remember, mastering fractions is a crucial building block for more advanced mathematical concepts. Continue to practice and explore, and you'll find yourself becoming more confident and proficient in this essential area of mathematics. The seemingly simple fraction 25/145, therefore, serves as a gateway to a deeper understanding of mathematical principles and their real-world relevance.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Of 145 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.