5000 X 50
stanleys
Sep 16, 2025 · 5 min read
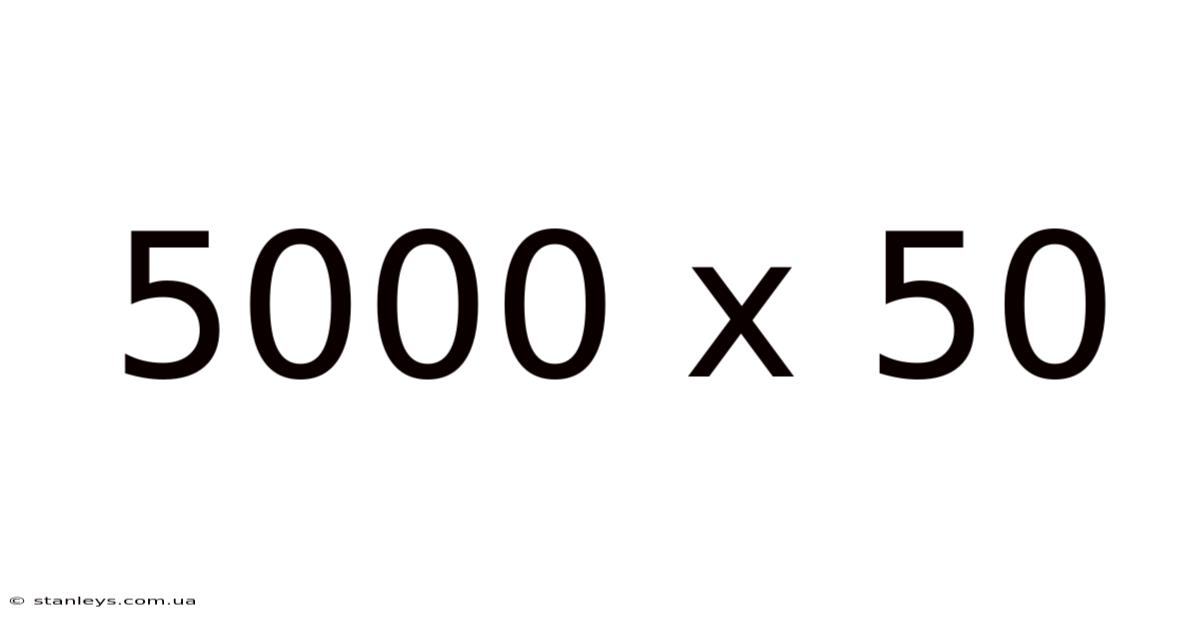
Table of Contents
Decoding 5000 x 50: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 5000 x 50, delving far beyond the basic arithmetic to uncover the underlying mathematical principles and its diverse applications in real-world scenarios. We will break down the calculation, examine different methods for solving it, and explore its relevance across various fields. Understanding this seemingly straightforward problem offers a gateway to comprehending more complex mathematical concepts and their practical uses. This comprehensive guide is perfect for students, educators, and anyone curious about the power and versatility of multiplication.
Understanding the Basics: Multiplication Fundamentals
At its core, 5000 x 50 represents repeated addition. It asks: "What is the sum of fifty 5000s?" This fundamental understanding is crucial, especially when working with larger numbers. Multiplication provides a concise and efficient way to handle such repetitive addition. The numbers involved, 5000 and 50, are called factors, and the result of the multiplication, 250,000, is called the product.
Methods for Solving 5000 x 50
Several methods can efficiently solve 5000 x 50. Let's explore a few:
1. Standard Multiplication Algorithm
This traditional method involves multiplying each digit of one factor by each digit of the other factor, carrying over when necessary. While straightforward, it can be time-consuming with larger numbers. For 5000 x 50:
- Multiply 0 (ones place of 5000) by 50: 0
- Multiply 0 (tens place of 5000) by 50: 0
- Multiply 0 (hundreds place of 5000) by 50: 0
- Multiply 5 (thousands place of 5000) by 50: 250,000
Therefore, 5000 x 50 = 250,000
2. Using the Distributive Property
The distributive property states that a(b + c) = ab + ac. We can use this to simplify the calculation:
5000 x 50 = 5000 x (5 x 10) = (5000 x 5) x 10 = 25000 x 10 = 250,000
3. Mental Math Techniques
With practice, mental math techniques can provide a quick solution. For instance:
- Recognize 50 as half of 100. Calculate 5000 x 100 (easily done by adding two zeros: 500,000), then halve the result: 500,000 / 2 = 250,000
4. Using Scientific or Standard Calculators
Modern calculators provide an effortless way to obtain the solution. Simply enter 5000 x 50 and press the equals sign.
Expanding the Concept: Applications of Multiplication in Real Life
The seemingly simple calculation of 5000 x 50 has wide-ranging practical applications across diverse fields:
1. Business and Finance
- Inventory Management: A company with 50 warehouses, each holding 5000 units of a particular product, needs to calculate total inventory. 5000 x 50 = 250,000 units.
- Payroll Calculations: If 50 employees each earn $5000 per month, the total monthly payroll is 5000 x 50 = $250,000.
- Profit Calculation: A product sells for $50, and 5000 units are sold. The total revenue is 5000 x 50 = $250,000.
2. Engineering and Construction
- Material Estimation: A construction project requires 5000 bricks per building, and there are 50 buildings. Total brick requirement: 5000 x 50 = 250,000 bricks.
- Area Calculation: A rectangular plot of land measures 5000 meters by 50 meters. Its area is 5000 x 50 = 250,000 square meters.
3. Science and Research
- Data Analysis: Researchers analyzing 50 datasets, each containing 5000 data points, have a total of 5000 x 50 = 250,000 data points to process.
- Laboratory Experiments: In experiments involving repeated measurements, calculating the total number of measurements (e.g., 5000 measurements per sample, with 50 samples).
4. Everyday Life
- Shopping: Buying 50 items priced at $5000 each.
- Travel: Calculating the total distance traveled if you drive 5000 km per trip for 50 trips.
Beyond the Numbers: Connecting to Higher Mathematical Concepts
Understanding 5000 x 50 lays the groundwork for more advanced mathematical concepts:
1. Exponents and Powers of Ten
The calculation can be viewed in terms of powers of ten. 5000 can be expressed as 5 x 10³, and 50 as 5 x 10¹. Thus:
(5 x 10³) x (5 x 10¹) = 25 x 10⁴ = 250,000
2. Scientific Notation
For very large or very small numbers, scientific notation is a useful tool. 5000 x 50 can be written as (5 x 10³) x (5 x 10¹) = 2.5 x 10⁵.
3. Algebra
The problem can be generalized algebraically: Let x = 5000 and y = 50. The calculation becomes xy = 250,000. This introduces the concept of variables and equations.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes students make when multiplying large numbers?
A: Common mistakes include errors in carrying over digits, misplacing decimal points (if dealing with decimal numbers), and not understanding place value.
Q: Are there any shortcuts for multiplying by 50?
A: Yes! Multiplying by 50 is the same as multiplying by 100 and then dividing by 2. This can often be done mentally.
Q: How can I improve my multiplication skills?
A: Practice is key! Regular practice with various multiplication problems, using different methods, and utilizing online resources or educational games can significantly improve your skills.
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental mathematical operation with applications in countless areas of life, from everyday finances to complex scientific calculations. A strong grasp of multiplication forms the basis for understanding more advanced mathematical concepts.
Conclusion: The Power of a Simple Calculation
The seemingly simple equation 5000 x 50 = 250,000 unveils a world of mathematical possibilities. By exploring its solution through various methods and examining its diverse applications, we've gained a deeper appreciation for the power and importance of multiplication. From fundamental arithmetic to advanced mathematical concepts and practical real-world scenarios, this calculation serves as a powerful illustration of the interconnectedness of mathematics and its relevance in our daily lives. The ability to perform this calculation efficiently and understand its underlying principles is a valuable skill applicable across numerous fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5000 X 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.