240 / 3
stanleys
Sep 15, 2025 · 6 min read
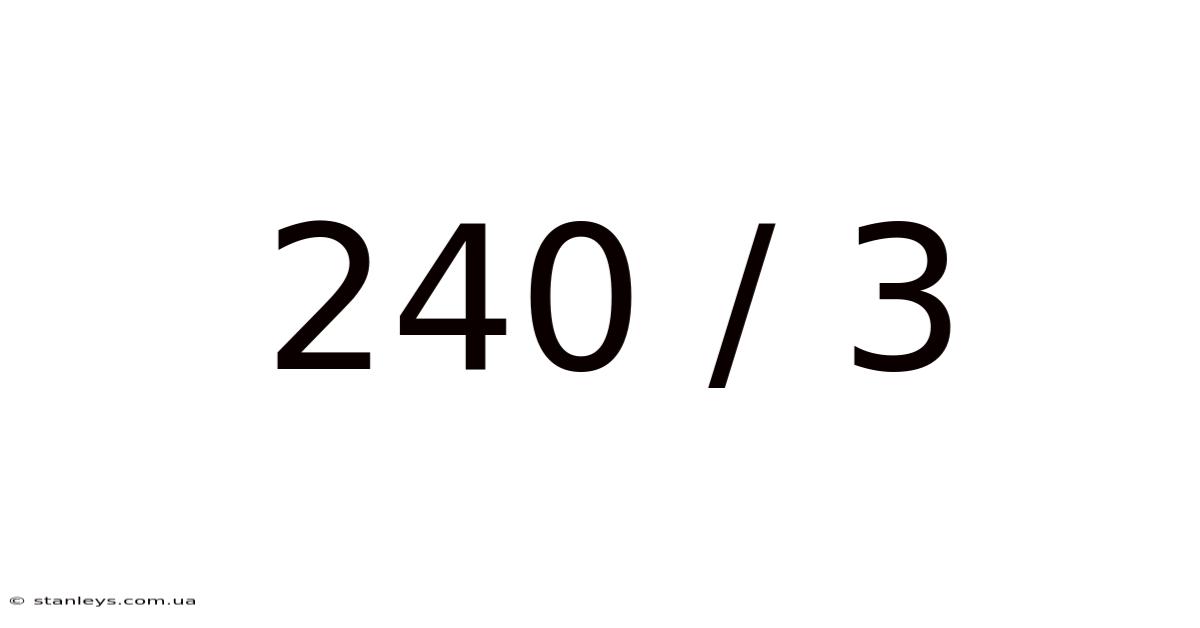
Table of Contents
Decoding 240 / 3: A Deep Dive into Division and its Applications
This article will explore the seemingly simple mathematical operation of 240 divided by 3 (240 / 3), going beyond the immediate answer to delve into the underlying principles, practical applications, and broader implications of division in mathematics and everyday life. We'll examine different methods for solving this problem, explore its relevance in various fields, and address frequently asked questions. Understanding this seemingly simple calculation opens doors to a more profound comprehension of numerical relationships and their significance.
I. Introduction: Understanding Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially represents the process of splitting a quantity into equal parts. In the context of 240 / 3, we are asking: "How many times does 3 go into 240?" or equivalently, "If we divide 240 into 3 equal groups, how many will be in each group?" The answer, as we'll demonstrate, is 80. But the journey to understanding why 80 is the answer is far more enriching than simply stating the result.
II. Methods for Solving 240 / 3
There are several approaches to solving this division problem, each offering a unique perspective and reinforcing different mathematical concepts:
A. Long Division: This classic method is a foundational skill in arithmetic. It systematically breaks down the division process into smaller, manageable steps.
80
3 | 240
-24
00
-0
0
- We start by dividing 3 into the first digit of the dividend (240), which is 2. Since 3 doesn't go into 2, we move to the next digit, forming the number 24.
- 3 goes into 24 eight times (3 x 8 = 24). We write the 8 above the 4.
- We subtract 24 from 24, leaving 0.
- We bring down the next digit, which is 0.
- 3 goes into 0 zero times. We write 0 above the 0.
- The final answer is 80.
B. Repeated Subtraction: This method visually demonstrates the concept of division as repeated subtraction. We repeatedly subtract 3 from 240 until we reach 0. The number of times we subtract 3 represents the quotient. While less efficient for larger numbers, it provides a clear conceptual understanding of division.
240 - 3 = 237 237 - 3 = 234 ...and so on until we reach 0. Counting the number of subtractions will yield 80.
C. Using Multiplication: Division and multiplication are inverse operations. To solve 240 / 3, we can ask: "What number, when multiplied by 3, equals 240?" Knowing multiplication tables, we can quickly determine that 3 x 80 = 240. Therefore, 240 / 3 = 80. This method is particularly efficient when dealing with easily recognizable multiplication facts.
D. Fractions: The division problem 240 / 3 can also be expressed as the fraction 240/3. Simplifying this fraction by dividing both the numerator (240) and the denominator (3) by their greatest common divisor (3) results in 80/1, which simplifies to 80. This approach strengthens understanding of the relationship between fractions and division.
III. Practical Applications of Division: Beyond the Classroom
The seemingly simple calculation of 240 / 3 has widespread applications across various fields:
A. Everyday Life:
- Sharing: Dividing 240 cookies among 3 friends equally results in each friend receiving 80 cookies.
- Measurement: Converting 240 inches into feet (since there are 12 inches in a foot, the calculation would be different, but demonstrates the practical application).
- Pricing: Determining the unit price of an item when 3 items cost $240.
- Recipe Scaling: Adjusting a recipe that serves 3 people to serve a larger group.
B. Business and Finance:
- Profit Sharing: Dividing profits among 3 partners.
- Cost Allocation: Distributing expenses equally among 3 departments.
- Inventory Management: Determining the number of units per shelf when 240 units need to be displayed on 3 shelves.
C. Science and Engineering:
- Data Analysis: Calculating averages or means from a dataset.
- Physics: Determining the average speed.
- Chemistry: Calculating molar mass.
D. Computer Science:
- Algorithm Design: Division is a fundamental operation in many algorithms and data structures.
- Data Structures: Hashing and indexing often rely on division.
IV. The Significance of Divisibility Rules
Understanding divisibility rules can significantly simplify calculations. Divisibility rules provide quick ways to determine if a number is divisible by another without performing the actual division. For example, a number is divisible by 3 if the sum of its digits is divisible by 3. In our case, 2 + 4 + 0 = 6, which is divisible by 3, confirming that 240 is divisible by 3. This knowledge speeds up calculations and fosters a deeper understanding of number properties.
V. Expanding the Concept: Beyond Whole Numbers
While we've focused on whole numbers, the principle of division applies equally to decimals and fractions. For instance, 240.6 / 3 would involve a similar process, but with decimal point considerations. Understanding division across different number systems is crucial for tackling more complex mathematical problems.
VI. Frequently Asked Questions (FAQ)
Q1: What if I have a remainder?
A: When dividing numbers, sometimes you'll have a remainder. For instance, if you divide 241 by 3, you get 80 with a remainder of 1. This remainder indicates that the division is not exact. The remainder can be expressed as a fraction (1/3) or a decimal (0.333...).
Q2: How can I improve my division skills?
A: Practice is key! Start with simpler division problems and gradually increase the difficulty. Regularly reviewing multiplication tables helps, as multiplication and division are closely linked. Utilize different methods like long division, repeated subtraction, and mental math techniques to build a solid understanding.
Q3: Are there any tricks or shortcuts for division?
A: Yes, understanding divisibility rules is a significant shortcut. Also, recognizing patterns and using estimation can speed up calculations. For example, realizing that 240 is close to 243 (3 x 81), allows for a quick estimation of the answer.
Q4: Why is division important?
A: Division is a fundamental mathematical operation with vast applications in various fields. It's essential for problem-solving, data analysis, and understanding numerical relationships. It helps us to distribute resources fairly, make accurate calculations, and comprehend complex systems.
VII. Conclusion: The Power of Understanding
The seemingly simple equation 240 / 3 = 80 serves as a gateway to understanding the broader principles of division and its far-reaching implications. By exploring different solution methods, examining practical applications, and addressing common questions, we've uncovered the profound significance of this fundamental mathematical operation. Mastering division is not merely about obtaining an answer; it's about developing critical thinking skills, enhancing problem-solving abilities, and gaining a deeper appreciation for the interconnectedness of mathematical concepts. This understanding empowers individuals to navigate various aspects of life more effectively, whether it's sharing resources, analyzing data, or tackling complex engineering challenges. It’s a foundational skill that lays the groundwork for advanced mathematical concepts and real-world applications. The journey of understanding 240 / 3 extends far beyond the simple answer of 80, revealing the rich and multifaceted nature of mathematics itself.
Latest Posts
Latest Posts
-
Minutes To Years
Sep 15, 2025
-
54 8kg To Stone
Sep 15, 2025
-
170kg In Lbs
Sep 15, 2025
-
64 1 3
Sep 15, 2025
-
24 X 6
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 240 / 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.