23 X 6
stanleys
Sep 17, 2025 · 6 min read
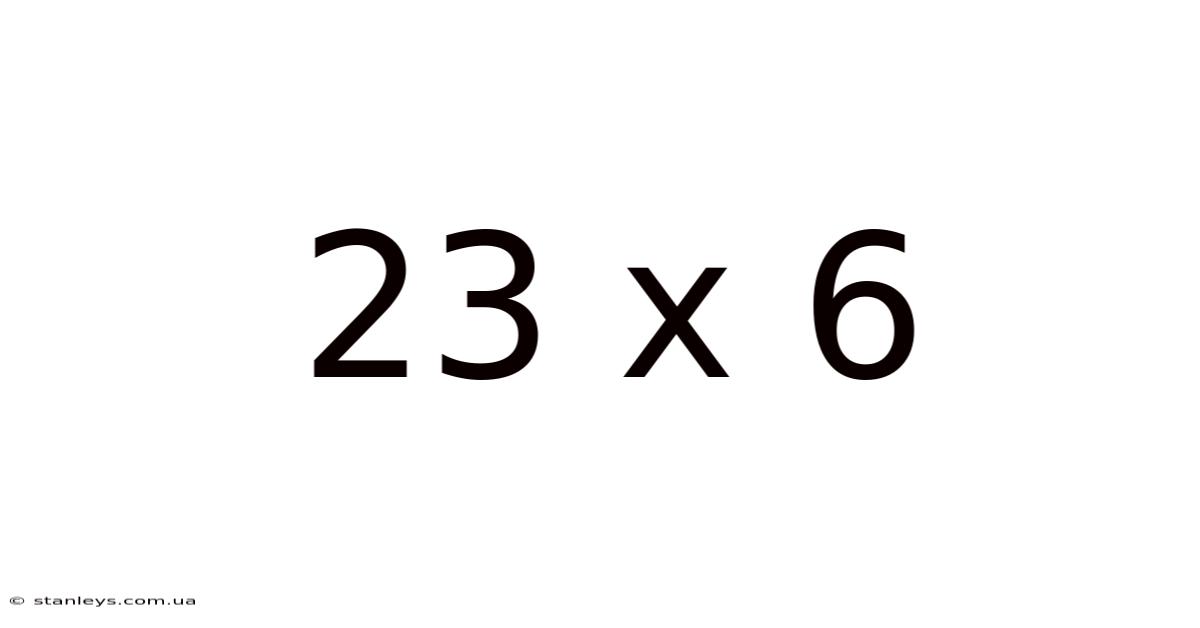
Table of Contents
Unveiling the Mysteries of 23 x 6: A Deep Dive into Multiplication
The seemingly simple multiplication problem, 23 x 6, holds within it a wealth of mathematical concepts and practical applications. This article will explore this seemingly straightforward calculation, delving into various methods of solving it, its relevance in different mathematical fields, and its connections to everyday life. We'll move beyond a simple answer and explore the underlying principles that make multiplication such a powerful tool.
Understanding the Fundamentals: What is Multiplication?
Before we tackle 23 x 6, let's briefly review the core concept of multiplication. Multiplication is essentially repeated addition. When we say 23 x 6, we're asking: "What is the result of adding 23 to itself six times?" This fundamental understanding forms the basis of all multiplication problems. It's the building block upon which more complex mathematical operations are constructed.
Visualizing this can be helpful. Imagine six rows of 23 objects each. Counting all the objects would give you the answer to 23 x 6. This visual representation helps to solidify the conceptual understanding of multiplication, especially for those new to the concept or those looking to reinforce their understanding of basic arithmetic.
Methods for Solving 23 x 6
There are several ways to approach solving 23 x 6. The most common methods include:
1. Traditional Multiplication:
This is the method most commonly taught in schools. It involves breaking down the numbers and multiplying each part separately, then adding the results.
- Step 1: Multiply the ones digit: 6 x 3 = 18. Write down the 8 and carry-over the 1.
- Step 2: Multiply the tens digit: 6 x 2 = 12. Add the carry-over 1: 12 + 1 = 13. Write down 13.
- Step 3: Combine the results: The final answer is 138.
2. Distributive Property:
This method leverages the distributive property of multiplication over addition. We can break down 23 into 20 + 3 and then multiply each part by 6:
- Step 1: (20 x 6) + (3 x 6) This breaks the problem into smaller, more manageable parts.
- Step 2: 120 + 18 This simplifies the calculation.
- Step 3: 138 This is the final answer. This method is particularly useful for mental calculations and highlights the underlying mathematical principles at play.
3. Lattice Multiplication:
This less common method uses a grid to organize the multiplication process. While it might seem more complex initially, it's a visually appealing and effective technique, particularly beneficial for larger multiplication problems.
- A grid is drawn with two columns (for the tens and ones digits of 23) and two rows (for the ones digit of 6).
- Each cell is divided diagonally.
- The individual multiplications (6 x 3 and 6 x 2) are performed and the results are written within their respective cells, with the tens digit above the diagonal and the ones digit below.
- Finally, the numbers are added diagonally, starting from the bottom right.
This method provides a clear and organized approach, minimizing errors, especially when dealing with larger numbers.
4. Repeated Addition:
As previously mentioned, multiplication is repeated addition. We can solve 23 x 6 by repeatedly adding 23 six times:
23 + 23 + 23 + 23 + 23 + 23 = 138
While straightforward, this method becomes less efficient for larger numbers. It's a valuable approach, however, for solidifying the fundamental connection between addition and multiplication.
23 x 6 in Different Mathematical Contexts
The seemingly simple calculation of 23 x 6 extends far beyond its basic application. Let's explore how it connects to broader mathematical concepts:
Algebra:
In algebra, we often encounter variables. Imagine the problem as 23 * x = 138. Finding the value of x would involve division (138 / 23 = 6), showing the inverse relationship between multiplication and division.
Geometry:
Consider a rectangle with sides of 23 units and 6 units. The area of this rectangle is calculated by multiplying the length and width: 23 x 6 = 138 square units. This demonstrates the application of multiplication in geometric calculations.
Number Theory:
The factors of 138 (1, 2, 3, 6, 23, 46, 69, 138) can be explored within the context of number theory. Understanding prime factorization (2 x 3 x 23) provides insights into the structure of the number 138 and its divisibility rules.
Real-World Applications of 23 x 6
The seemingly abstract concept of multiplying 23 by 6 has numerous practical applications in our daily lives:
- Shopping: If an item costs $23 and you buy six of them, the total cost is $138.
- Measurement: If you need 23 feet of rope for a project and you need six such lengths, you'll need a total of 138 feet.
- Cooking: If a recipe calls for 23 grams of an ingredient and you’re making six batches, you will need 138 grams.
- Data Analysis: Imagine a survey with 23 respondents in each of six groups. Multiplying 23 by 6 will give you the total number of respondents (138).
These examples demonstrate how even simple multiplication problems like 23 x 6 are integral to numerous aspects of our daily lives, highlighting the practical value of mathematical skills.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to multiply 23 x 6?
A: The easiest way depends on individual preference and mathematical comfort. The traditional method is widely taught and generally efficient. The distributive property is excellent for mental math.
Q: Are there any tricks to make multiplication faster?
A: Practice and familiarity are key. Understanding the distributive property and learning multiplication tables helps significantly.
Q: Why is learning multiplication important?
A: Multiplication is a fundamental building block in mathematics. It's essential for problem-solving in various fields, from everyday calculations to complex scientific applications.
Q: What if I struggle with multiplication?
A: Don't be discouraged! Practice is crucial. Use various methods, seek help from teachers or tutors, and utilize online resources to build your understanding and confidence.
Conclusion: Beyond the Numbers
The seemingly simple problem of 23 x 6 opens a window into the fascinating world of mathematics. It's more than just a calculation; it's a demonstration of fundamental mathematical principles, a tool for problem-solving in various contexts, and a connection to our everyday lives. By understanding the various methods of solving this problem and exploring its broader implications, we gain a deeper appreciation for the power and elegance of mathematics. Remember, the key to mastering multiplication, and indeed any mathematical concept, lies in understanding the underlying principles and practicing regularly. The more you engage with the subject, the more confident and proficient you will become. So, keep exploring, keep practicing, and keep discovering the beauty of numbers!
Latest Posts
Latest Posts
-
Larkin Building Buffalo
Sep 17, 2025
-
70 Of 32
Sep 17, 2025
-
Decimal Of 5 9
Sep 17, 2025
-
Liter Water Weight
Sep 17, 2025
-
Best Nail Wraps
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 23 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.