70 Of 32
stanleys
Sep 17, 2025 · 5 min read
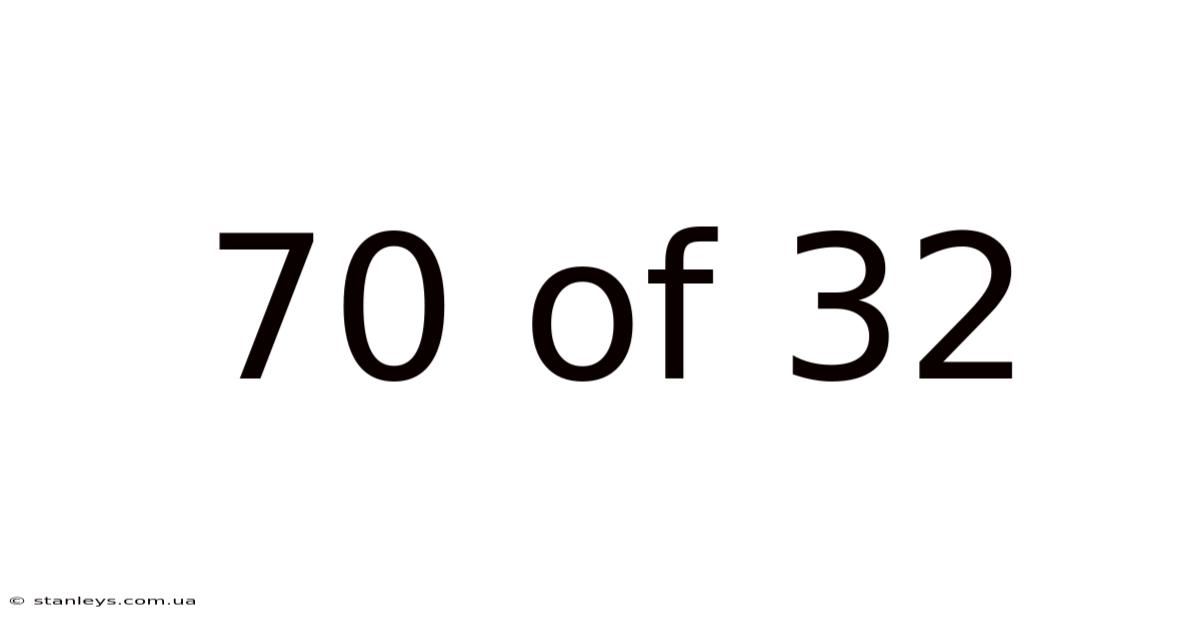
Table of Contents
Decoding the Fraction: Understanding 70/32 and its Implications
What does 70/32 mean? At first glance, it seems like a simple fraction, but understanding its implications requires delving into the world of mathematics, specifically fractions, decimals, and percentages. This article will not only explain what 70/32 represents but also explore its various forms, interpretations, and practical applications, providing a comprehensive understanding suitable for learners of all levels. We will cover simplifying the fraction, converting it to a decimal and percentage, and discuss its use in real-world scenarios.
Understanding the Basics: Fractions Explained
Before diving into 70/32, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number, representing the part) and the denominator (the bottom number, representing the whole). In our case, 70 is the numerator and 32 is the denominator. This means we have 70 parts out of a possible 32 parts. Since the numerator is larger than the denominator, we have an improper fraction, indicating a value greater than one.
Simplifying 70/32: Finding the Greatest Common Divisor (GCD)
Improper fractions are often simplified to make them easier to understand and work with. Simplification involves finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder. To find the GCD of 70 and 32, we can use the Euclidean algorithm or list the factors of each number.
Let's use the Euclidean algorithm:
- Divide 70 by 32: 70 = 2 * 32 + 6
- Replace 70 with 32 and 32 with the remainder 6: 32 = 5 * 6 + 2
- Replace 32 with 6 and 6 with the remainder 2: 6 = 3 * 2 + 0
The last non-zero remainder is 2, which is the GCD of 70 and 32.
Now we can simplify the fraction by dividing both the numerator and the denominator by the GCD:
70 ÷ 2 = 35 32 ÷ 2 = 16
Therefore, the simplified fraction is 35/16.
Converting 70/32 to a Decimal: Division is Key
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
70 ÷ 32 = 2.1875
So, 70/32 is equal to 2.1875. This decimal representation provides a more readily understandable numerical value, particularly for calculations involving other decimal numbers.
Expressing 70/32 as a Percentage: Multiplying by 100
Percentages are another way of representing fractions and decimals. To convert a fraction or decimal to a percentage, we multiply by 100%.
Using the decimal form:
2.1875 * 100% = 218.75%
Therefore, 70/32 is equivalent to 218.75%. This shows that 70/32 represents more than double the original value (100%).
Mixed Numbers: A Different Perspective
Improper fractions can also be expressed as mixed numbers. A mixed number consists of a whole number and a proper fraction. To convert 35/16 (the simplified form of 70/32) into a mixed number, we perform the division:
35 ÷ 16 = 2 with a remainder of 3
This means that 35/16 can be written as 2 3/16. This representation clearly shows that 70/32 is equal to two whole units and three-sixteenths of another unit.
Real-World Applications of 70/32
The fraction 70/32, or its equivalent forms, can appear in various real-world scenarios. For instance:
-
Ratio and Proportion: Imagine a scenario where 70 students scored above average on a test, out of a total of 32 students. The fraction 70/32 highlights the significantly high proportion of students performing above average.
-
Measurement and Units: If you are working with measurements, 70/32 could represent a ratio of lengths, volumes, or weights. For example, if you have a rope of 70 centimeters and you cut it into 32 equal pieces, each piece would be 70/32 centimeters long.
-
Financial Calculations: Percentages are commonly used in finance. If an investment grows from an initial value of 32 units to 70 units, then the growth rate is represented by 70/32 or 218.75%.
-
Data Analysis and Statistics: Fractions and percentages are crucial for analyzing data and expressing results. 70/32 could be part of a statistical report, expressing the ratio of successes to attempts in a given experiment.
Further Exploration: Advanced Concepts
Understanding 70/32 opens the door to exploring more advanced mathematical concepts. Here are some areas to delve deeper:
-
Rational Numbers: Fractions are rational numbers, numbers that can be expressed as a ratio of two integers. Understanding rational numbers is essential for algebra and calculus.
-
Continued Fractions: Complex fractions can be expressed as continued fractions, which can provide interesting insights and approximations. 70/32 could be converted into a continued fraction to explore different numerical representations.
-
Proportionality and Ratios: Understanding the concept of proportionality and ratios is crucial for various applications, including geometry, physics, and engineering.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 70/32?
A: The simplest form of 70/32 is 35/16.
Q: How do I convert 70/32 to a decimal?
A: Divide 70 by 32 to get 2.1875.
Q: What is 70/32 as a percentage?
A: 70/32 is equal to 218.75%.
Q: Can 70/32 be expressed as a mixed number?
A: Yes, 70/32 (or its simplified form 35/16) can be expressed as the mixed number 2 3/16.
Conclusion: A Deeper Understanding of Fractions
This article has provided a comprehensive exploration of the fraction 70/32, covering its simplification, conversion to decimals and percentages, its representation as a mixed number, and its various applications. Understanding fractions is fundamental to various mathematical and real-world applications. By exploring this single fraction, we’ve touched upon core concepts that build the foundation for more advanced mathematical understanding. The journey from a simple fraction to understanding its multifaceted nature highlights the power and elegance of mathematics. Remember, the key is to break down complex problems into smaller, manageable steps. This approach, applied consistently, will empower you to tackle even more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
0 32 As Fraction
Sep 17, 2025
-
64 5kg In Pounds
Sep 17, 2025
-
Avenge Vs Revenge
Sep 17, 2025
-
2 X 128
Sep 17, 2025
-
William Shakespeare Statue
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.