23 X 3
stanleys
Sep 16, 2025 · 6 min read
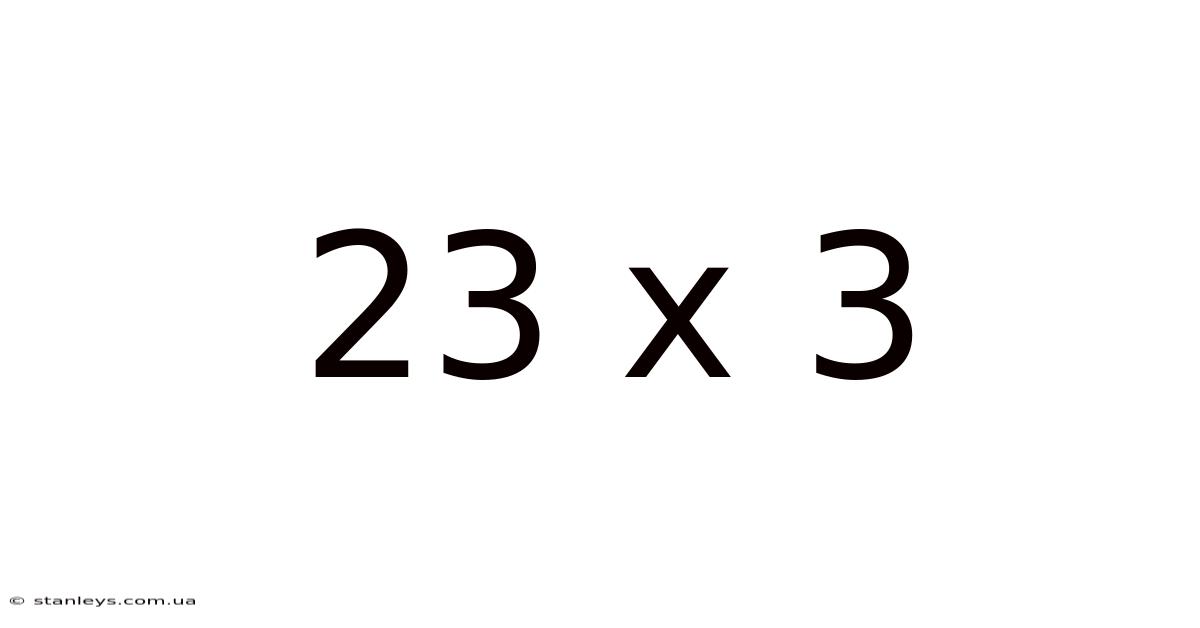
Table of Contents
Exploring the Simple Calculation: 23 x 3 – A Deep Dive into Multiplication
This article explores the seemingly simple calculation of 23 x 3, delving beyond the immediate answer to illuminate the underlying mathematical principles and practical applications. We'll examine different methods of solving this problem, highlighting their efficiency and demonstrating how this basic calculation forms a foundational block for more complex mathematical concepts. This exploration is beneficial for anyone looking to solidify their understanding of multiplication, particularly for students and educators working with elementary arithmetic.
Introduction: Understanding Multiplication
Multiplication, at its core, is repeated addition. When we say 23 x 3, we are essentially adding 23 to itself three times: 23 + 23 + 23. This understanding is crucial for grasping the fundamental nature of multiplication and for visualizing the operation. While seemingly straightforward for this small number, this principle scales to much larger multiplications. Understanding this foundational concept lays the groundwork for understanding more complex algebraic and arithmetic operations.
Method 1: Standard Multiplication Algorithm
The standard algorithm, taught in most elementary schools, involves breaking down the multiplication into smaller, manageable steps. Let's apply this to 23 x 3:
-
Multiply the ones place: 3 (from 23) multiplied by 3 (from the multiplier) equals 9. Write down 9.
-
Multiply the tens place: 2 (from 23) multiplied by 3 (from the multiplier) equals 6. Write down 6 to the left of 9.
-
Combine the results: The result is 69.
Therefore, 23 x 3 = 69. This method is efficient and systematic, making it ideal for teaching multiplication to beginners. It emphasizes place value – a critical component in understanding larger numbers and operations.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down 23 x 3:
-
Decompose 23: Rewrite 23 as 20 + 3.
-
Apply the distributive property: 3 x (20 + 3) = (3 x 20) + (3 x 3)
-
Solve the smaller multiplications: (3 x 20) = 60 and (3 x 3) = 9
-
Add the results: 60 + 9 = 69
This method demonstrates a deeper understanding of mathematical properties and offers a more flexible approach to multiplication, especially useful when dealing with larger numbers. This method helps build an intuitive understanding of how multiplication interacts with addition, paving the way for understanding more complex algebraic manipulations later.
Method 3: Repeated Addition
As mentioned earlier, multiplication is fundamentally repeated addition. For 23 x 3, we simply add 23 three times:
23 + 23 + 23 = 69
This method, while seemingly simple for small numbers like this, reinforces the core concept of multiplication. It's a highly visual and concrete method, particularly beneficial for young learners who are still developing their understanding of abstract mathematical concepts. While less efficient for larger numbers, it's a valuable tool for building a strong foundational understanding.
Method 4: Lattice Multiplication
Lattice multiplication is a visual method that can be helpful for understanding the process of multiplying multi-digit numbers. Although less common than the standard algorithm, it offers a unique approach:
-
Create a lattice: Draw a grid with two rows (for the digits of 23) and one column (for the multiplier 3).
-
Multiply and split: Multiply each digit of 23 by 3. Split the result into tens and ones, placing the digits diagonally within the corresponding cell. For example, 3 x 2 = 6, which is placed as 0 in the top half and 6 in the bottom half of the cell. 3 x 3 = 9, which is placed as 0 in the top half and 9 in the bottom half.
-
Sum the diagonals: Add the numbers along the diagonals, starting from the bottom right. The first diagonal sums to 9, the second diagonal sums to 6.
-
Combine the sums: The result, reading from left to right, is 69.
Lattice multiplication is a visually appealing method that can aid in understanding place value and the distribution of multiplication across digits. This method can be particularly helpful for visualizing the multiplication process, especially when dealing with larger numbers. It also reduces the likelihood of errors by breaking down the multiplication process into smaller, more manageable steps.
Real-World Applications of 23 x 3
While seemingly trivial, the multiplication of 23 x 3 has practical applications in everyday life. Consider these examples:
- Shopping: If you buy three items costing $23 each, the total cost is $69.
- Measurement: If you have three lengths of rope, each 23 meters long, the total length is 69 meters.
- Counting: If you have 23 groups of 3 items each, you have a total of 69 items.
- Recipe Scaling: If a recipe calls for 23 grams of an ingredient and you want to triple the recipe, you need 69 grams.
These examples highlight the pervasive presence of simple multiplication in daily life, underscoring the importance of mastering this fundamental operation. It’s a building block for more complex calculations across numerous fields, from finance to engineering.
Further Exploration: Expanding the Concept
Understanding 23 x 3 opens doors to understanding more complex mathematical concepts. Consider these extensions:
-
Multiplication of larger numbers: The principles used to solve 23 x 3 directly apply to multiplying larger numbers. The standard algorithm, distributive property, and even lattice multiplication scale effectively.
-
Algebraic expressions: Understanding multiplication is essential for solving algebraic equations and simplifying expressions. The ability to manipulate and simplify expressions involving multiplication forms a foundation for more advanced mathematical concepts.
-
Geometry: Calculating areas and volumes often involves multiplication. Understanding basic multiplication is crucial for tackling geometric problems, from calculating the area of a rectangle to finding the volume of a rectangular prism.
-
Fractions and decimals: The principles of multiplication extend to fractions and decimals, requiring a slightly adapted approach but fundamentally utilizing the same underlying concepts.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate 23 x 3?
A: The easiest way depends on your comfort level. The standard algorithm is generally efficient and widely taught. Repeated addition is conceptually simple, while the distributive property reveals deeper mathematical principles.
Q: Why is understanding multiplication important?
A: Multiplication is fundamental to many aspects of mathematics and its practical applications. It's a building block for more advanced mathematical concepts and essential for problem-solving in various fields.
Q: Are there other methods to multiply 23 by 3?
A: While the methods described above are common, other less conventional methods exist. Some involve using visual aids or different organizational strategies, but all ultimately rely on the core principle of repeated addition or its equivalent.
Q: Can this be solved using a calculator?
A: Yes, a calculator can quickly provide the answer. However, understanding the underlying mathematical principles is far more valuable than simply obtaining the numerical result.
Conclusion: The Significance of Simple Calculations
While the calculation of 23 x 3 may seem elementary, its exploration unveils a wealth of mathematical principles and practical applications. Mastering this fundamental operation builds a solid foundation for tackling more complex calculations and opens doors to a deeper understanding of the world around us. The different methods presented highlight the versatility and richness of even the simplest arithmetic operations. By exploring these different approaches, we not only arrive at the answer (69) but also gain a far richer and more nuanced understanding of the underlying mathematical principles at play. The ability to approach a problem from multiple perspectives is a valuable skill, transferable far beyond the realm of elementary arithmetic.
Latest Posts
Related Post
Thank you for visiting our website which covers about 23 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.