200 Of 5
stanleys
Sep 17, 2025 · 5 min read
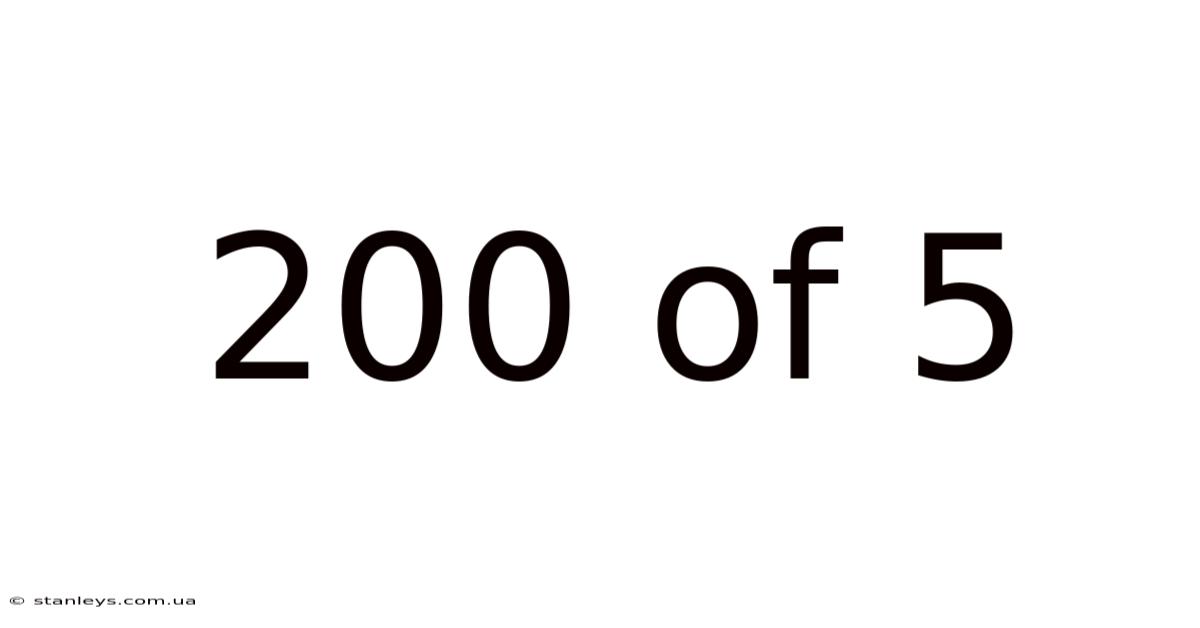
Table of Contents
Decoding the Fraction: Understanding 200/5 and its Implications
What does 200/5 mean? At first glance, it might seem like a simple division problem. And it is! But understanding 200/5 goes beyond simply getting the answer; it's about grasping the fundamental concepts of fractions, division, and their application in various contexts. This article will delve deep into this seemingly simple fraction, exploring its meaning, its calculation, and its relevance in different areas of mathematics and beyond. We'll also address common misconceptions and answer frequently asked questions to ensure a comprehensive understanding.
Understanding Fractions: A Foundation
Before we dive into 200/5, let's establish a solid understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many parts make up the whole.
For instance, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) indicates that two parts make up the whole. This means we have one out of two equal parts.
Calculating 200/5: Different Approaches
There are several ways to calculate 200/5. The most straightforward is through direct division.
Method 1: Direct Division
The simplest approach is to divide the numerator (200) by the denominator (5). This can be done manually, using a calculator, or even through mental math if you're comfortable with your multiplication tables.
200 ÷ 5 = 40
Therefore, 200/5 simplifies to 40. This means that 200 is equivalent to 40 groups of 5.
Method 2: Simplifying the Fraction
Before dividing, you could simplify the fraction. While not strictly necessary in this case, it can be helpful with larger or more complex fractions. Simplifying involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD of 200 and 5 is 5.
200 ÷ 5 = 40 5 ÷ 5 = 1
This simplifies the fraction to 40/1, which is still equal to 40.
Method 3: Repeated Subtraction
This method is less efficient for larger numbers but provides a valuable conceptual understanding of division. Repeatedly subtract the denominator (5) from the numerator (200) until you reach zero. The number of times you subtract is the answer.
200 - 5 = 195 195 - 5 = 190 ...and so on until you reach 0. You'll find you've subtracted 5 forty times.
The Significance of 40: Interpreting the Result
The result of 200/5, which is 40, has significant implications depending on the context.
-
In pure mathematics: 40 is simply the equivalent whole number representation of the fraction 200/5.
-
In real-world applications: Imagine you have 200 apples, and you want to divide them equally among 5 friends. Each friend would receive 40 apples. Similarly, if you drive 200 miles in 5 hours, your average speed is 40 miles per hour.
-
In scaling and proportions: The fraction 200/5 represents a ratio or proportion. If a recipe calls for 5 cups of flour to make a cake, and you want to make a larger cake using 200 cups of flour, you've scaled the recipe by a factor of 40 (200/5 = 40). You would need to multiply all other ingredients in the recipe by 40 as well.
Expanding the Concept: Working with Fractions
The example of 200/5 provides a solid foundation for understanding more complex fraction operations. Let's explore some related concepts:
-
Improper Fractions and Mixed Numbers: An improper fraction is one where the numerator is larger than the denominator (e.g., 200/5). A mixed number combines a whole number and a proper fraction (e.g., 40 0/1). In this case, 200/5 is an improper fraction that simplifies to the whole number 40.
-
Adding and Subtracting Fractions: To add or subtract fractions, you need a common denominator. For instance, adding 1/2 + 1/4 requires finding a common denominator (4) and rewriting the fractions as 2/4 + 1/4 = 3/4.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction and then multiplying.
Addressing Common Misconceptions
Several misconceptions often arise when working with fractions. Here are some crucial points to clarify:
-
The denominator cannot be zero: Dividing by zero is undefined in mathematics. A fraction with a denominator of zero is meaningless.
-
Fractions represent parts of a whole: Remember, fractions are not just numbers; they represent parts of a whole. Understanding this concept is crucial for applying fractions to real-world situations.
-
Simplifying fractions doesn't change their value: Simplifying a fraction simply reduces it to its lowest terms, making it easier to work with, but it doesn't alter its actual value.
Frequently Asked Questions (FAQ)
Q: What if the numerator wasn't divisible by the denominator?
A: If the numerator isn't perfectly divisible by the denominator, you'll get a fraction as the result. For example, 201/5 would be 40 1/5.
Q: How can I convert a decimal to a fraction?
A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (e.g., 0.4 = 4/10). Then simplify the fraction if possible.
Q: How do I solve word problems involving fractions?
A: Carefully read the word problem, identify the key information (the numerator and denominator), and then set up the appropriate fraction or equation to solve the problem.
Conclusion: The Broader Significance of Understanding 200/5
While seemingly simple, the fraction 200/5 offers a powerful entry point to understanding core mathematical concepts. Mastering fractions is fundamental to success in various areas, including algebra, calculus, and even everyday life. Beyond the simple calculation of 40, this article aimed to highlight the underlying principles and practical applications of fractions. By grasping these fundamentals, you'll build a stronger foundation in mathematics and improve your ability to solve problems efficiently and effectively. Remember, understanding the 'why' behind the 'how' is key to true mathematical literacy. So, the next time you encounter a fraction, don't just calculate the answer; take a moment to appreciate the rich concepts it embodies.
Latest Posts
Latest Posts
-
Stihl Ts 400
Sep 17, 2025
-
Larkin Building Buffalo
Sep 17, 2025
-
70 Of 32
Sep 17, 2025
-
Decimal Of 5 9
Sep 17, 2025
-
Liter Water Weight
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 200 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.