5.7 Of 134
stanleys
Sep 14, 2025 · 5 min read
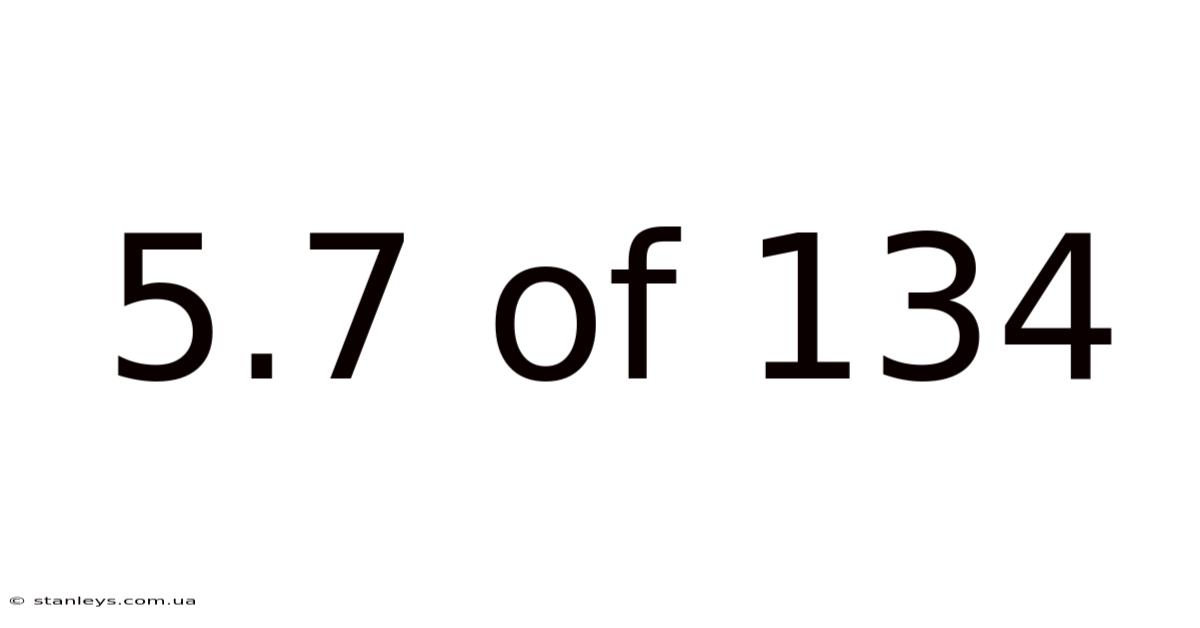
Table of Contents
Decoding 5.7 of 134: Understanding Proportions, Percentages, and Their Applications
This article delves into the meaning and implications of the statement "5.7 of 134," exploring its representation as a proportion, percentage, and fraction, and demonstrating its relevance in various real-world scenarios. We'll move beyond simple calculation to understand the underlying concepts and their application in fields ranging from statistics and finance to everyday life. Understanding proportions and percentages is crucial for making informed decisions and interpreting data accurately.
Understanding the Basics: Proportions and Percentages
Before diving into the specifics of "5.7 of 134," let's establish a solid foundation in proportions and percentages. A proportion is a statement of equality between two ratios. A ratio compares two quantities, while a percentage expresses a proportion as a fraction of 100. For instance, the ratio 1:4 can be expressed as the fraction 1/4, which is equivalent to 25%.
The statement "5.7 of 134" indicates a part (5.7) relative to a whole (134). To understand its meaning fully, we need to convert this into different representations:
-
Fraction: The simplest representation is a fraction: 5.7/134. This clearly shows the part (5.7) as a fraction of the whole (134).
-
Decimal: Dividing 5.7 by 134 gives us a decimal representation, approximately 0.0425. This represents the proportion of 5.7 out of 134.
-
Percentage: To express this as a percentage, we multiply the decimal by 100: 0.0425 * 100 = 4.25%. This means that 5.7 represents approximately 4.25% of 134.
Calculating and Interpreting 5.7 of 134
Now, let's break down the calculations and explore different interpretations of "5.7 of 134."
1. Direct Calculation:
The most straightforward approach is to calculate the percentage directly:
(5.7 / 134) * 100 ≈ 4.25%
This tells us that 5.7 is approximately 4.25% of 134.
2. Contextual Interpretation:
The interpretation of "5.7 of 134" is heavily dependent on the context. Consider these scenarios:
-
Test Scores: If 134 represents the total number of questions on a test, and a student answered 5.7 correctly (perhaps some questions were partially correct), then the student achieved a score of approximately 4.25%. This would be a low score, indicating a need for improvement.
-
Survey Results: Imagine a survey with 134 respondents. If 5.7 respondents answered a particular question in a specific way, this represents a small proportion (4.25%) of the total respondents. Further analysis might be needed to determine the significance of this finding.
-
Financial Data: In a financial context, 134 could represent the total investment, and 5.7 could represent a profit or loss. A 4.25% profit might be considered small, while a 4.25% loss might be significant depending on the overall risk tolerance.
-
Scientific Measurements: In scientific research, 134 could represent the total number of samples, and 5.7 could represent the number of samples exhibiting a particular characteristic. The percentage (4.25%) would help in determining the prevalence of that characteristic within the sample population.
Expanding on the Concepts: Proportions in Real-World Applications
The concept of proportions extends far beyond simple calculations. Understanding proportions is fundamental to:
-
Statistics: Proportions are used extensively in statistical analysis to represent sample proportions, confidence intervals, and effect sizes. Understanding proportions helps in interpreting statistical data and drawing meaningful conclusions.
-
Finance: Proportions are vital in finance for portfolio allocation, risk management, and return on investment calculations. Investors use proportions to determine the appropriate allocation of assets across different investment classes.
-
Probability: Proportions are central to probability theory. For example, the probability of an event occurring can be expressed as a proportion.
-
Scaling and Ratios: Architects, engineers, and designers use proportions and ratios extensively for scaling blueprints, models, and designs.
-
Cooking and Baking: Recipes frequently use proportions to adjust ingredient quantities based on the number of servings required. A clear understanding of proportions ensures accurate scaling of recipes.
-
Mapping and Cartography: Maps use scales based on proportions to represent geographic areas on a smaller surface.
Advanced Considerations: Dealing with Fractional Values
The inclusion of the decimal value 5.7 raises the question of how to handle fractional values in proportion calculations. In many real-world scenarios, fractional values are perfectly acceptable and often represent more precise measurements. For instance, in the case of survey responses, it's possible to have partial responses that are meaningfully incorporated.
Frequently Asked Questions (FAQ)
Q1: How do I calculate the percentage if the numbers aren't whole numbers?
A1: You calculate it the same way. Divide the part by the whole, then multiply by 100. For example, (5.7 / 134) * 100 ≈ 4.25%. The presence of decimals doesn't change the fundamental process.
Q2: What if the "part" is larger than the "whole"?
A2: This indicates an error in the data or interpretation. A proportion cannot have a part larger than the whole. Review your data and ensure accuracy. If the data is correct, it might represent a different relationship entirely that needs to be defined.
Q3: How can I improve my understanding of proportions and percentages?
A3: Practice is key! Try solving various proportion problems, starting with simple examples and gradually increasing the complexity. Look for real-world examples in your daily life where proportions are used. Online resources and educational materials can also be very helpful.
Q4: Are there any tools or software to assist with these calculations?
A4: While simple calculators are sufficient for basic calculations, spreadsheet software like Microsoft Excel or Google Sheets offers more advanced features for handling larger datasets and performing more complex calculations involving proportions and percentages.
Conclusion: The Power of Proportionate Thinking
The seemingly simple statement "5.7 of 134" opens up a world of mathematical concepts and practical applications. Understanding proportions and percentages is not just about performing calculations; it's about developing a framework for analyzing data, making informed decisions, and interpreting the world around us more effectively. By mastering these fundamental concepts, you equip yourself with essential tools for navigating a data-driven world and tackling various challenges in different fields. From everyday tasks to complex scientific analyses, the ability to understand and utilize proportions and percentages is an invaluable skill. Continue practicing, exploring real-world examples, and building your confidence in handling these essential mathematical concepts.
Latest Posts
Latest Posts
-
4 Of 50
Sep 14, 2025
-
750ml En Oz
Sep 14, 2025
-
20 Of 21
Sep 14, 2025
-
Calcium Carbonate Hydrochloric
Sep 14, 2025
-
Factorise 6x 4
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5.7 Of 134 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.