18.5 Of 986
stanleys
Sep 11, 2025 · 5 min read
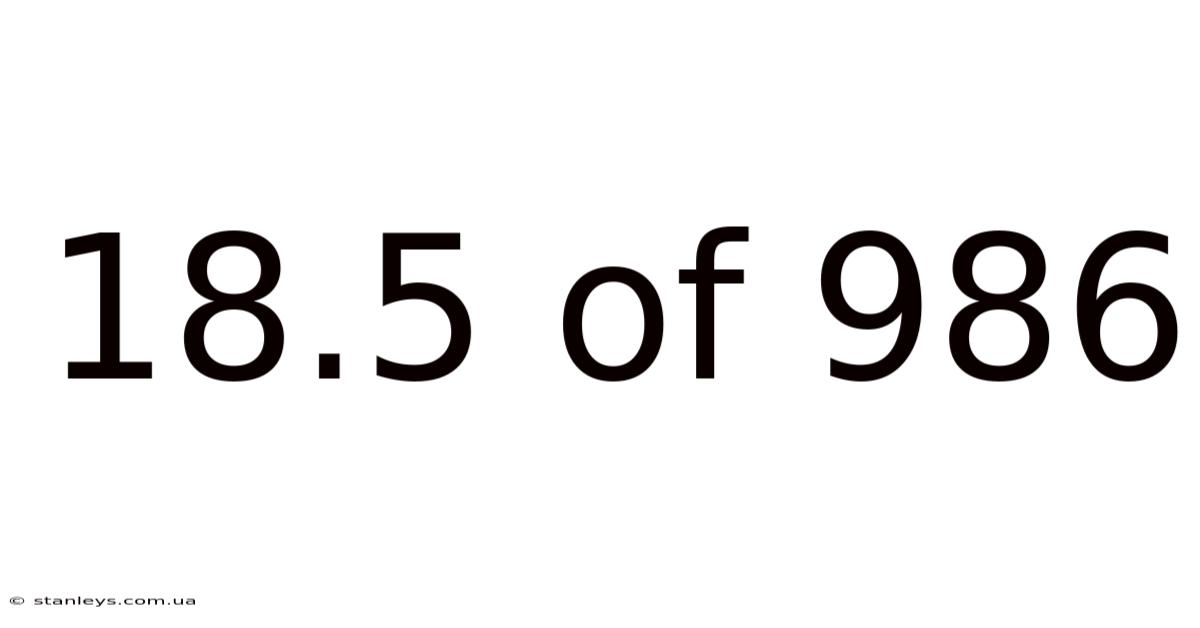
Table of Contents
Decoding 18.5 of 986: Understanding Proportions and Percentages
This article delves into the meaning and calculation of "18.5 of 986," exploring the concepts of proportions, percentages, and their applications in various fields. We'll unpack the problem, providing a step-by-step guide to solving it and illustrating its relevance in everyday life, from understanding financial data to interpreting scientific results. Understanding these calculations is crucial for informed decision-making in numerous contexts.
Understanding the Problem: What Does "18.5 of 986" Mean?
The phrase "18.5 of 986" signifies a proportional relationship. It asks: what is the value that represents 18.5 units out of a total of 986 units? This is a fundamental question in mathematics that has wide-ranging applications. We can approach this problem in two primary ways: calculating the fraction and converting it to a percentage.
Method 1: Calculating the Fraction
The most straightforward method is to express "18.5 of 986" as a fraction. This fraction represents the part (18.5) compared to the whole (986). The calculation is simple:
18.5 / 986
Using a calculator, we find that:
18.5 / 986 ≈ 0.01872
This decimal represents the fraction of 986 that 18.5 constitutes. It means that 18.5 is approximately 0.01872 times the size of 986.
Method 2: Calculating the Percentage
Converting the fraction to a percentage provides a more readily understandable representation. To do this, we multiply the decimal result by 100:
0.01872 * 100 ≈ 1.872%
Therefore, 18.5 is approximately 1.872% of 986. This percentage signifies that 18.5 represents a small portion (less than 2%) of the total value of 986.
Applications and Real-World Examples
The ability to calculate proportions and percentages like "18.5 of 986" is essential across numerous disciplines:
-
Finance: Imagine you're analyzing investment returns. If your portfolio had a total value of 986 units (e.g., shares, dollars) and your profit was 18.5 units, you can easily calculate your return on investment (ROI) using this method. Understanding this percentage helps assess the success of the investment.
-
Science and Statistics: In scientific research, data often involves large datasets. Calculating percentages and proportions is essential for representing the significance of experimental results. For example, if a researcher surveys 986 participants and finds 18.5 exhibit a specific trait, this percentage helps determine the prevalence of that trait within the study population.
-
Business and Economics: Market share analysis, sales figures, and consumer behavior analysis heavily rely on calculating percentages and proportions. If a company holds 18.5% of a market of 986 units (e.g., number of customers), this reveals their competitive standing.
-
Everyday Life: Even everyday tasks, like calculating tips or discounts, use these fundamental mathematical concepts. If a bill totals 986 units and you wish to leave an 18.5% tip, the calculation follows the same process.
Understanding the Concept of Proportions
Proportions are mathematical relationships that compare two ratios. In the case of "18.5 of 986," we have a ratio of 18.5 to 986. This ratio can be expressed as a fraction (18.5/986) and simplified, or expressed as a percentage (approximately 1.872%). Understanding proportions allows us to solve problems where one quantity is directly proportional to another. This means that if one quantity increases, the other increases proportionally, and vice-versa.
Working with Decimals and Percentages
Decimal numbers and percentages are essential tools for expressing proportions. Decimals represent fractions where the denominator is a power of 10 (e.g., 10, 100, 1000). Percentages are simply decimals multiplied by 100, adding a % symbol to denote the proportion relative to 100. These representations are crucial for simplifying the interpretation of numerical data and facilitating comparisons.
The Significance of Accuracy
While we've used approximations in the calculations, the exact value of 18.5/986 is a recurring decimal. The level of accuracy required depends on the context. In some applications (e.g., financial calculations), high precision is crucial. In others, an approximation might suffice. Always consider the context to determine the appropriate level of precision in your calculations.
Beyond Simple Calculations: Exploring Further Applications
The basic calculation of "18.5 of 986" opens doors to more complex scenarios:
-
Inverse Proportions: This contrasts with direct proportion. Here, if one quantity increases, the other decreases proportionally. Imagine the relationship between speed and travel time.
-
Compound Proportions: These involve more than two variables that are proportionally related. Consider the relationship between area, length, and width.
-
Ratio and Proportion Problems: These problems require solving for an unknown quantity within a proportional relationship. This often involves cross-multiplication to find the solution.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator for this calculation? A: Absolutely! Calculators simplify the process, especially with decimals.
-
Q: Is it always necessary to convert the result to a percentage? A: Not necessarily. Depending on the context, a decimal fraction might be more appropriate. The choice depends on the desired level of clarity and the specific application.
-
Q: What if the numbers are much larger? A: The principles remain the same. You can still use a calculator or spreadsheet software to handle the calculations efficiently.
-
Q: Are there other methods to solve this type of problem? A: Yes, you can use ratios and proportions to solve similar problems. You could set up a proportion: 18.5/x = 986/100, and solve for x to find the percentage directly.
Conclusion
Understanding the relationship between "18.5 of 986" and how to calculate this proportion using both fractions and percentages is a fundamental skill applicable across numerous disciplines. Whether it's assessing financial returns, interpreting scientific data, or solving everyday problems, mastering these calculations is crucial for making informed decisions and developing a deeper understanding of quantitative information. Remember to always consider the context of the problem and the desired level of accuracy when working with proportions and percentages. Practice is key to becoming proficient in these essential mathematical concepts. From simple calculations to more complex proportional relationships, this foundational knowledge will serve you well in various aspects of your life.
Latest Posts
Latest Posts
-
16 20 Simplified
Sep 11, 2025
-
38kg In Pounds
Sep 11, 2025
-
5 Of 250
Sep 11, 2025
-
48kg To Stones
Sep 11, 2025
-
Wizard Oz Gifts
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 18.5 Of 986 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.