14 X 2
stanleys
Sep 11, 2025 · 6 min read
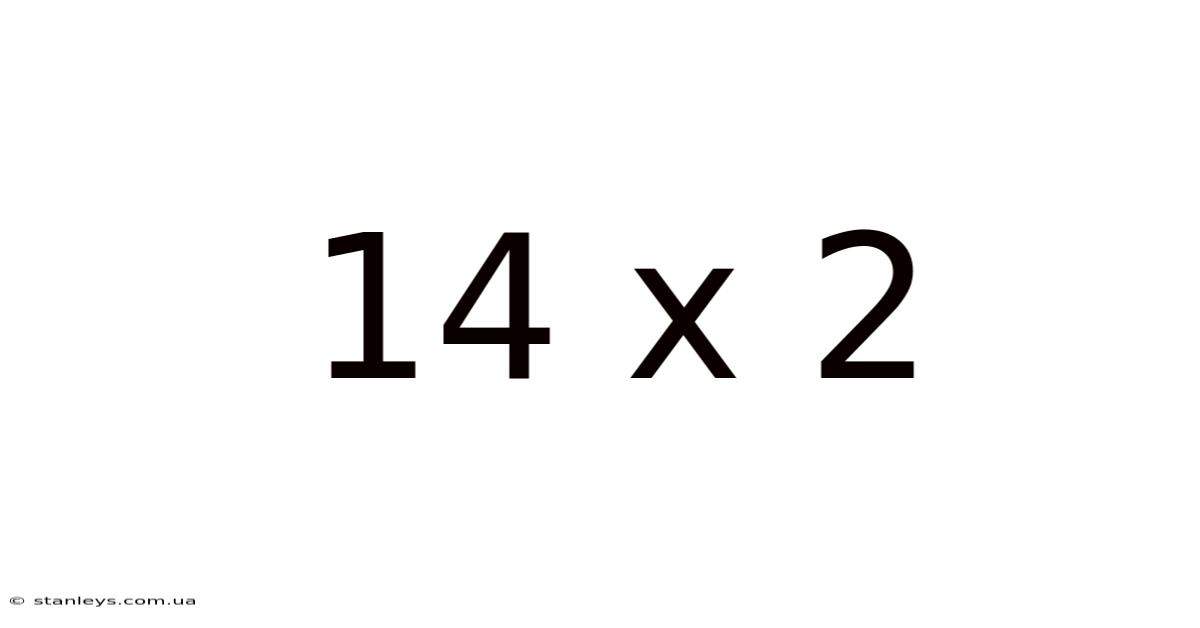
Table of Contents
Unveiling the Mysteries of 14 x 2: A Deep Dive into Multiplication
This article explores the seemingly simple calculation of 14 x 2, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll journey from basic multiplication techniques to advanced concepts, demonstrating how this seemingly elementary problem forms the foundation for more complex mathematical operations. Understanding 14 x 2 is more than just getting the right answer; it's about grasping the fundamental building blocks of arithmetic.
Introduction: Beyond the Obvious Answer
At first glance, 14 x 2 appears trivial. A quick calculation reveals the answer: 28. However, this seemingly simple equation offers a rich opportunity to explore various mathematical concepts and their practical relevance. This article will delve into different methods for solving this problem, examining the underlying principles and highlighting the significance of understanding multiplication in broader mathematical contexts. We will cover everything from basic arithmetic to more advanced concepts, ensuring a comprehensive understanding for readers of all levels.
Method 1: The Standard Multiplication Algorithm
The most common method for solving 14 x 2 involves the standard multiplication algorithm taught in elementary schools. This involves multiplying each digit of the first number (14) by the second number (2) and then adding the results:
- Step 1: Multiply the units digit of 14 (which is 4) by 2: 4 x 2 = 8
- Step 2: Multiply the tens digit of 14 (which is 1) by 2: 1 x 2 = 2
- Step 3: Combine the results: 20 + 8 = 28
Therefore, 14 x 2 = 28. This method is straightforward and provides a solid foundation for understanding multiplication. It emphasizes place value – the position of a digit in a number determines its value.
Method 2: Repeated Addition
Multiplication can be visualized as repeated addition. 14 x 2 means adding 14 to itself two times:
14 + 14 = 28
This method is particularly helpful for beginners, as it provides a concrete visual representation of multiplication. It directly connects multiplication to the more intuitive concept of addition. This approach is useful for building a strong understanding of the fundamental relationship between addition and multiplication.
Method 3: Distributive Property
The distributive property of multiplication over addition is a crucial concept in algebra and beyond. It states that a(b + c) = ab + ac. We can apply this to our problem by breaking down 14 into 10 + 4:
2 x (10 + 4) = (2 x 10) + (2 x 4) = 20 + 8 = 28
This method demonstrates a more sophisticated understanding of multiplication, highlighting the flexibility and power of algebraic principles even in seemingly simple calculations. Understanding the distributive property is essential for more advanced mathematical operations.
Method 4: Using a Number Line
A number line provides a visual representation of the multiplication process. Start at 0, and move 14 units to the right twice. This will land you at 28. This visual method aids in comprehension, especially for those who benefit from visual learning styles. It clearly demonstrates the repeated addition aspect of multiplication.
The Significance of Place Value
The problem 14 x 2 subtly highlights the importance of place value. The number 14 represents 1 ten and 4 units. When multiplied by 2, we essentially multiply both the tens and units place separately, then combine the results. This concept forms the basis for understanding larger multiplication problems. A strong grasp of place value is crucial for success in mathematics.
Extending the Concept: Multiplication and its Applications
Understanding 14 x 2 is a stepping stone to tackling more complex calculations. This fundamental understanding forms the basis for:
- Larger multiplications: The principles applied to 14 x 2 are directly applicable to multiplying larger numbers. The standard algorithm, repeated addition, and distributive property all scale to handle more complex calculations.
- Algebra: The distributive property, demonstrated in solving 14 x 2, is a cornerstone of algebraic manipulation. It's used extensively in solving equations and simplifying expressions.
- Geometry: Multiplication is fundamental in calculating areas and volumes. For instance, finding the area of a rectangle requires multiplying its length and width.
- Real-world applications: Multiplication is used in countless everyday scenarios, from calculating costs (e.g., the total cost of 14 items costing $2 each) to determining distances and quantities.
Practical Applications: Real-World Examples
The seemingly simple calculation of 14 x 2 has numerous real-world applications:
- Shopping: If you buy 14 apples at $2 each, the total cost is 14 x 2 = $28.
- Baking: If a recipe calls for 14 cups of flour and you need to double the recipe, you'll need 14 x 2 = 28 cups of flour.
- Construction: If you need to lay 14 rows of bricks with 2 bricks per row, you'll need 14 x 2 = 28 bricks.
- Travel: If you travel at an average speed of 14 miles per hour for 2 hours, you'll travel 14 x 2 = 28 miles.
These are just a few examples of how this simple calculation appears in everyday life, highlighting the practical relevance of even basic arithmetic.
Frequently Asked Questions (FAQ)
-
Q: What are some different ways to solve 14 x 2?
- A: We’ve explored several methods: the standard algorithm, repeated addition, the distributive property, and using a number line. Each method offers a different perspective and reinforces understanding.
-
Q: Why is understanding place value important when solving 14 x 2?
- A: Place value helps us understand the value of each digit in the number 14 (1 ten and 4 units). Multiplying each place value separately and then adding the results ensures accuracy.
-
Q: How does this simple problem relate to more complex mathematical concepts?
- A: The principles behind solving 14 x 2, such as the distributive property and understanding place value, are fundamental to more advanced mathematical concepts in algebra, geometry, and calculus.
-
Q: What are some real-world applications of this calculation?
- A: Numerous everyday situations involve this calculation, including shopping, baking, construction, and travel, demonstrating the practical relevance of basic mathematics.
Conclusion: The Power of Fundamentals
The seemingly simple equation 14 x 2 serves as a microcosm of the broader world of mathematics. By exploring various methods for solving this problem, we've uncovered underlying principles that are essential for understanding more complex mathematical operations. Mastering fundamental concepts, like those demonstrated in this simple multiplication problem, lays the groundwork for future success in mathematics and its diverse applications in the real world. The ability to approach even simple problems from multiple angles fosters a deeper understanding and strengthens mathematical intuition. This, in turn, equips individuals with the problem-solving skills needed to tackle more challenging mathematical tasks and real-world situations with confidence. So, while the answer to 14 x 2 is 28, the true value lies in the understanding and appreciation of the mathematical principles involved.
Latest Posts
Latest Posts
-
98 2f To C
Sep 11, 2025
-
4kg In Grams
Sep 11, 2025
-
0 75 X 3
Sep 11, 2025
-
127lbs To Kg
Sep 11, 2025
-
1000 Times 1000
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 14 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.