14 X 14
stanleys
Sep 11, 2025 · 6 min read
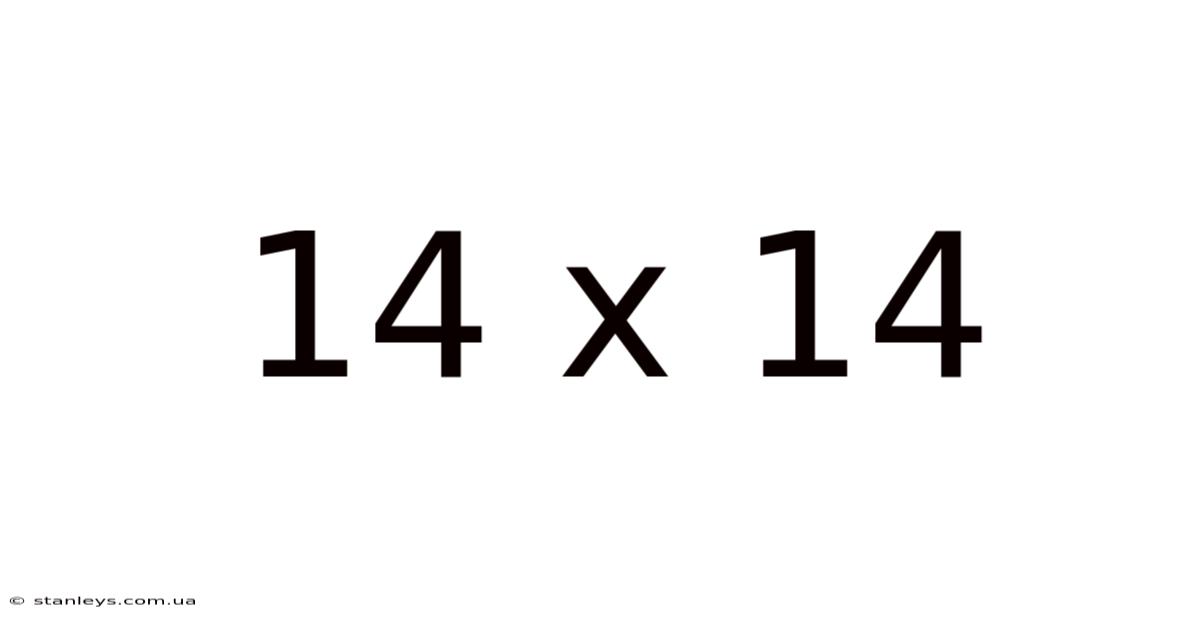
Table of Contents
Decoding 14 x 14: A Deep Dive into Multiplication, Area, and Beyond
The seemingly simple expression "14 x 14" opens a door to a surprisingly rich world of mathematical concepts. It's more than just a multiplication problem; it's a gateway to understanding area calculation, the properties of squares, and even the foundations of algebra. This article will explore the various facets of 14 x 14, from basic arithmetic to more advanced applications, ensuring a comprehensive understanding for learners of all levels.
I. The Fundamentals: Calculating 14 x 14
At its core, 14 x 14 is a multiplication problem. We're finding the product of 14 multiplied by itself. The most straightforward approach is using the standard multiplication algorithm:
14
x 14
----
56 (14 x 4)
140 (14 x 10)
----
196
Therefore, 14 x 14 = 196. This basic calculation forms the foundation for many more complex mathematical applications. We can also achieve this result using other methods like distributive property, breaking it down to (10 + 4) x (10 + 4) and expanding it using the FOIL method.
II. Visualizing 14 x 14: The Concept of Area
The result of 14 x 14, 196, takes on a powerful visual representation when considering the concept of area. Imagine a perfect square with sides measuring 14 units each (units could be centimeters, meters, inches, etc.). The area of this square, representing the space it occupies, is precisely 196 square units. This is because the area of a square is calculated by multiplying the length of one side by itself (side x side). This visualization makes the abstract concept of multiplication more tangible and relatable. We can even draw a grid of 14 x 14 squares to visually confirm this calculation.
This connection between multiplication and area is crucial in various fields, from geometry and architecture to computer graphics and cartography. Understanding how 14 x 14 relates to the area of a square provides a solid foundation for more advanced spatial reasoning.
III. Exploring Related Concepts: Squares and Square Roots
14 x 14 directly relates to the concept of perfect squares. A perfect square is a number that can be obtained by squaring an integer (multiplying an integer by itself). In this case, 196 is a perfect square because it's the result of 14 squared (14²). Understanding perfect squares is fundamental in algebra and number theory.
Conversely, the square root of 196 is 14. The square root of a number is a value that, when multiplied by itself, gives the original number. This inverse relationship between squaring and finding the square root is an essential concept in mathematics. It's also important to note that √196 = ±14, as both 14 and -14, when squared, result in 196.
IV. Expanding the Horizons: Applications of 14 x 14
While seemingly simple, the calculation and understanding of 14 x 14 extends far beyond basic arithmetic. Here are several applications across different fields:
-
Geometry: As discussed, calculating the area of squares is a direct application. This extends to calculating the area of more complex shapes that can be broken down into squares or rectangles. Think of tiling a floor, designing a building's foundation, or even creating pixel art.
-
Algebra: The concept of squaring numbers and finding square roots is crucial in solving quadratic equations. Understanding 14 x 14 strengthens the foundational understanding needed to tackle more complex algebraic problems.
-
Data Analysis: When dealing with square matrices (matrices with equal number of rows and columns) in data analysis, the concept of squares and square roots become important in various computations and transformations.
-
Computer Science: In computer graphics and image processing, understanding area calculation is fundamental to manipulating and rendering images. The concept of a 14 x 14 grid could represent a small image or texture.
-
Real-World Applications: Calculating the area of a room to determine the amount of flooring needed, estimating the area of a garden to plan planting, or determining the amount of paint needed for a wall are all real-world applications of this fundamental calculation.
V. Beyond the Numbers: Developing Mathematical Thinking
The seemingly simple calculation of 14 x 14 provides a robust opportunity to develop crucial mathematical thinking skills:
-
Problem-Solving: Finding different ways to arrive at the answer (using the standard algorithm, distributive property, visual representation) enhances problem-solving abilities.
-
Abstract Reasoning: Connecting the abstract concept of multiplication to the tangible concept of area fosters abstract reasoning skills.
-
Pattern Recognition: Exploring perfect squares and their properties allows for the recognition of numerical patterns.
-
Critical Thinking: Analyzing the different approaches to solving the problem encourages critical thinking about efficiency and accuracy.
VI. Frequently Asked Questions (FAQs)
-
Q: What are some alternative ways to calculate 14 x 14?
- A: Besides the standard algorithm, you can use the distributive property [(10 + 4) x (10 + 4)], using the FOIL method (First, Outer, Inner, Last) to expand the expression, or even utilize a calculator.
-
Q: What is the importance of understanding perfect squares?
- A: Understanding perfect squares is fundamental in algebra, number theory, and geometry. They simplify calculations and help identify patterns in numbers.
-
Q: How does 14 x 14 relate to the area of a square?
- A: The result, 196, directly represents the area of a square with sides of length 14 units. This connection is crucial for understanding spatial reasoning and solving geometric problems.
-
Q: Are there any real-world applications beyond area calculation?
- A: Yes, many applications exist, including volume calculations (for cubes), data analysis (matrices), computer graphics (pixel manipulation), and various engineering and design applications.
-
Q: Why is it important to learn different methods for multiplication?
- A: Learning multiple methods strengthens understanding and problem-solving skills. Different methods can be more efficient depending on the specific problem.
VII. Conclusion: The Enduring Power of 14 x 14
While the calculation of 14 x 14 might seem trivial at first glance, its implications are far-reaching. It serves as a fundamental building block for more complex mathematical concepts, from area calculation and algebra to data analysis and computer science. Understanding this seemingly simple calculation not only strengthens arithmetic skills but also enhances crucial mathematical thinking abilities, making it a cornerstone of mathematical literacy. The journey from basic multiplication to the vast applications of 14 x 14 showcases the interconnectedness of mathematical ideas and their importance in various fields. By exploring this calculation in detail, we unlock a deeper appreciation for the beauty and power of mathematics. The seemingly simple 196 square units holds a multitude of mathematical significance, waiting to be discovered and explored.
Latest Posts
Latest Posts
-
20 Of 26
Sep 11, 2025
-
90 Of 60
Sep 11, 2025
-
Front Panel Connectors
Sep 11, 2025
-
82 8kg In Stone
Sep 11, 2025
-
Rock Cycle Diagram
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 14 X 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.