136 Of 92
stanleys
Sep 09, 2025 · 6 min read
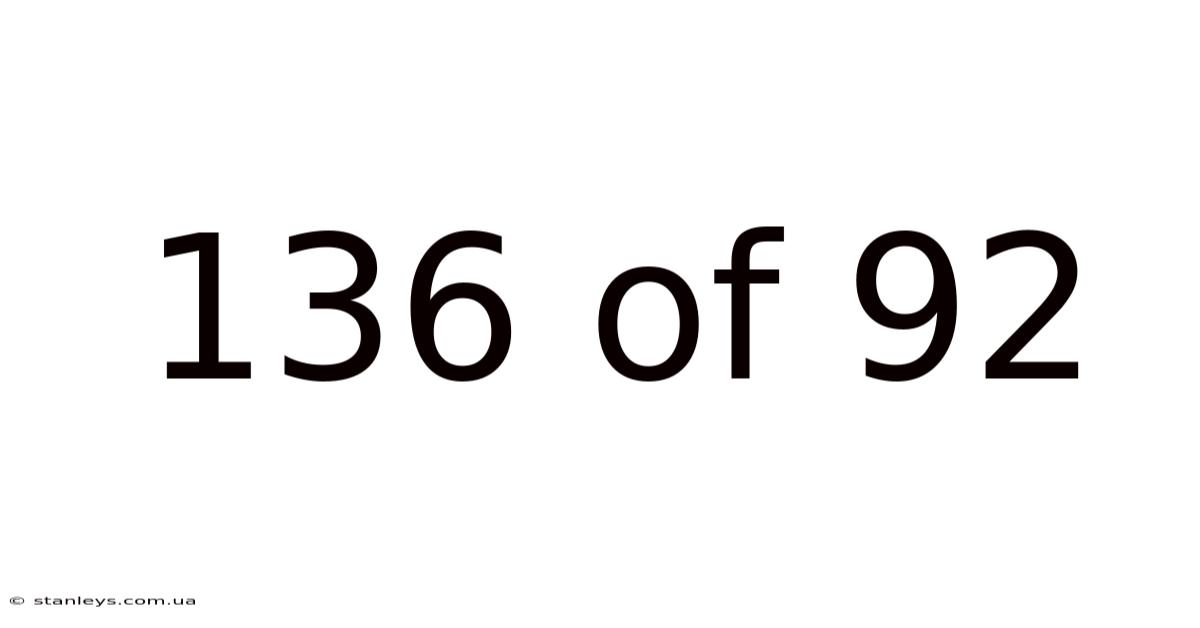
Table of Contents
Decoding the Enigma: Understanding the Fraction 136/92
The fraction 136/92 might seem like a simple mathematical expression, but it holds within it a wealth of concepts crucial to understanding fundamental arithmetic, fractions, ratios, percentages, and even basic algebra. This article will delve deep into the meaning and implications of this fraction, exploring its simplification, decimal equivalent, percentage representation, and practical applications. We'll also explore how understanding this seemingly simple fraction can build a stronger foundation in mathematics.
Introduction: Why 136/92 Matters
At first glance, 136/92 might appear insignificant. However, mastering the manipulation and interpretation of fractions like this is foundational to advanced mathematical concepts. Understanding its simplification, decimal representation, and percentage equivalent allows for a deeper comprehension of proportional reasoning – a skill applicable across various fields, from cooking and construction to finance and data analysis. This seemingly simple fraction serves as a microcosm of larger mathematical principles. Let's dissect it step-by-step.
Step-by-Step Simplification: Finding the Greatest Common Divisor (GCD)
The first step in working with any fraction is simplification. This involves reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator (136) and the denominator (92). The GCD is the largest number that divides both numbers without leaving a remainder.
Several methods exist for finding the GCD. One common method is the Euclidean algorithm:
-
Divide the larger number (136) by the smaller number (92): 136 ÷ 92 = 1 with a remainder of 44.
-
Replace the larger number with the smaller number (92) and the smaller number with the remainder (44): Now we have 92 and 44.
-
Repeat the process: 92 ÷ 44 = 2 with a remainder of 4.
-
Continue until the remainder is 0: 44 ÷ 4 = 11 with a remainder of 0.
The last non-zero remainder (4) is the GCD of 136 and 92.
Alternatively, we can find the prime factorization of both numbers:
- 136 = 2 x 2 x 2 x 17 = 2³ x 17
- 92 = 2 x 2 x 23 = 2² x 23
The common factors are 2². Therefore, the GCD is 2 x 2 = 4.
Now we can simplify the fraction:
136 ÷ 4 / 92 ÷ 4 = 34/23
The simplified fraction is 34/23. This is the most concise and efficient representation of the original fraction.
Converting to Decimal: Understanding the Value
To convert the simplified fraction 34/23 to a decimal, we perform the division: 34 ÷ 23 ≈ 1.478. This decimal representation provides a different perspective on the value of the fraction. It shows that 136/92 represents a quantity slightly larger than one and a half.
The approximation symbol (≈) is used because the decimal representation of 34/23 is a recurring decimal, meaning the digits after the decimal point repeat infinitely. The exact decimal value is 1.47826086956521739... For most practical applications, rounding to a suitable number of decimal places (e.g., 1.48) is sufficient.
Calculating the Percentage: Expressing the Fraction as a Proportion
Expressing the fraction as a percentage provides yet another way to understand its value. To convert a fraction to a percentage, we multiply the decimal equivalent by 100:
1.478 x 100 ≈ 147.8%
This means that 136/92 represents 147.8% of the denominator (92). This percentage representation is useful for comparing quantities and proportions. It highlights that 136 is significantly larger than 92, exceeding it by approximately 48%.
The Concept of Ratio: Comparing Quantities
The fraction 136/92 can also be interpreted as a ratio. A ratio expresses the relationship between two quantities. In this case, the ratio is 136:92, indicating that for every 92 units of one quantity, there are 136 units of another. This ratio can be simplified to 34:23, maintaining the same proportional relationship.
Ratios are used extensively in various fields. For instance, in a recipe, a ratio of 2:1 for flour to sugar indicates that for every 2 cups of flour, 1 cup of sugar is required. Understanding ratios is essential for scaling recipes, calculating proportions in construction, and analyzing data in many different contexts.
Practical Applications: Real-World Scenarios
The fraction 136/92, and its simplified form 34/23, finds applications in numerous real-world scenarios.
-
Scaling Recipes: Imagine a recipe that calls for 92 grams of butter and 136 grams of flour. If you want to make a larger batch, you can use the ratio 34:23 to scale up the ingredients proportionally.
-
Financial Calculations: In finance, ratios are used extensively. For instance, the debt-to-equity ratio compares a company's debt to its equity. Understanding fractions is vital for interpreting and analyzing these financial ratios.
-
Data Analysis: When analyzing datasets, proportions and percentages are frequently employed. Understanding fractions helps in accurately calculating and interpreting these proportions.
-
Construction and Engineering: Accurate proportions are essential in construction and engineering. Whether mixing concrete or calculating the dimensions of a structure, precise calculations involving fractions are crucial.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 136/92?
- A: The simplest form is 34/23.
-
Q: Is 136/92 an improper fraction?
- A: Yes, it is an improper fraction because the numerator (136) is larger than the denominator (92).
-
Q: How do I convert 136/92 to a mixed number?
- A: Divide 136 by 92. The quotient is 1, and the remainder is 44. Therefore, the mixed number is 1 44/92. This can be further simplified to 1 11/23.
-
Q: What is the decimal equivalent of 34/23?
- A: Approximately 1.478.
-
Q: What is the percentage equivalent of 136/92?
- A: Approximately 147.8%.
Advanced Concepts: Expanding Mathematical Understanding
Understanding 136/92 extends beyond basic arithmetic. It serves as a springboard for grasping more complex mathematical concepts:
-
Algebraic Manipulation: Fractions are crucial in algebraic equations. Solving equations often involves manipulating fractions to isolate variables.
-
Calculus: Calculus, the study of change, relies heavily on the concept of limits, which are often expressed using fractions.
-
Probability and Statistics: Fractions and percentages are fundamental to probability and statistics, used to express probabilities and proportions in data analysis.
Conclusion: A Foundation for Future Learning
The seemingly simple fraction 136/92 offers a rich learning opportunity. Through its simplification, conversion to decimal and percentage, and interpretation as a ratio, we've explored foundational mathematical concepts. Mastering these concepts builds a strong base for more advanced mathematical studies and practical applications in various fields. The journey from 136/92 to its simplified form 34/23 and its various representations demonstrates the power of understanding fundamental arithmetic principles. This understanding doesn't merely solve a single fraction; it unlocks a broader comprehension of mathematics and its role in our world. The ability to manipulate and interpret fractions, as demonstrated with this example, is a crucial skill for success in numerous academic and professional pursuits. Remember, even seemingly simple concepts, when explored thoroughly, can reveal surprising depth and significance.
Latest Posts
Latest Posts
-
Peri Arrest Meaning
Sep 10, 2025
-
75 Of 25
Sep 10, 2025
-
50ml In Tablespoons
Sep 10, 2025
-
King George Avenue
Sep 10, 2025
-
47 5kg In Stone
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 136 Of 92 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.