75 Of 25
stanleys
Sep 10, 2025 · 6 min read
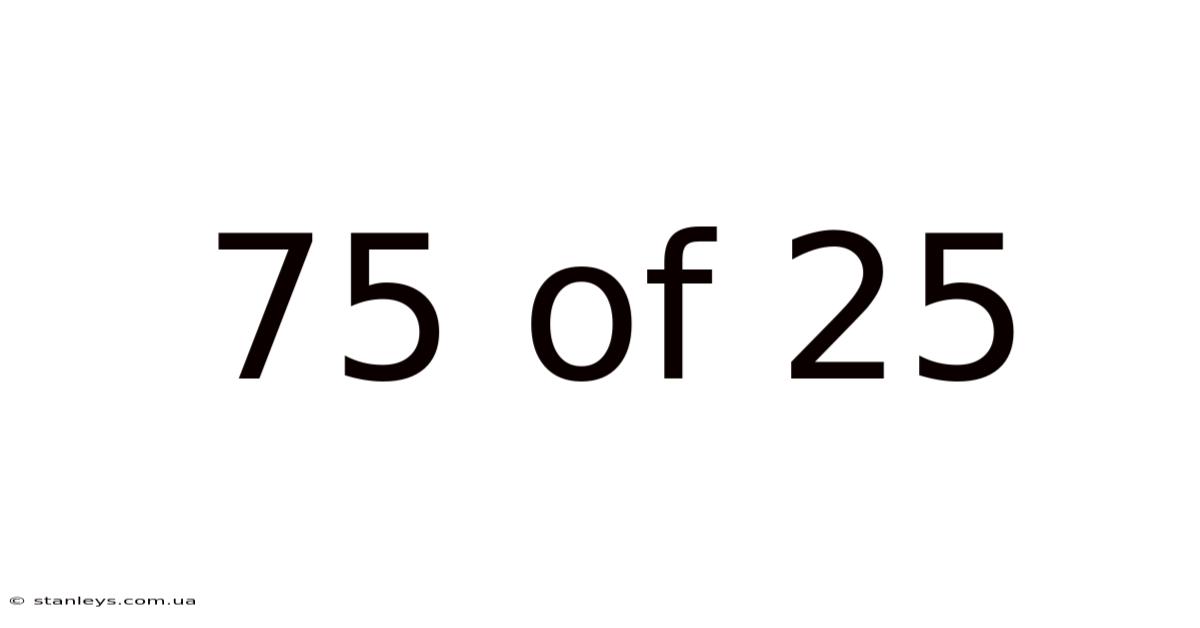
Table of Contents
Decoding the Fraction: Understanding 75/25 and its Implications
The seemingly simple fraction 75/25 often presents itself in various mathematical contexts, from basic arithmetic to more advanced applications. Understanding this fraction thoroughly involves not only calculating its value but also grasping its implications within different mathematical frameworks and real-world scenarios. This article will delve deep into the meaning, simplification, decimal representation, percentage equivalence, and applications of 75/25, providing a comprehensive understanding for learners of all levels.
I. Introduction: What is 75/25?
75/25 represents a fraction, a mathematical expression indicating the division of 75 (the numerator) by 25 (the denominator). Fractions are fundamental building blocks in mathematics, representing parts of a whole or ratios between two quantities. In the case of 75/25, we're essentially asking: "What is the result when 75 is divided into 25 equal parts?" Understanding this simple question unlocks a wealth of knowledge about the fraction's properties and its various uses. This fraction is particularly interesting because it simplifies to a whole number, showcasing a key concept in fraction manipulation.
II. Simplifying the Fraction: Finding the Lowest Terms
Before delving into more complex concepts, it's crucial to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by that number. The GCD of 75 and 25 is 25.
-
Step 1: Find the GCD of 75 and 25. This is easily determined since 25 is a factor of 75 (75 = 25 x 3). Therefore, the GCD is 25.
-
Step 2: Divide both the numerator and the denominator by the GCD: 75 ÷ 25 = 3 and 25 ÷ 25 = 1.
-
Step 3: The simplified fraction is 3/1, which is equivalent to 3. This means that 75/25 simplifies to the whole number 3.
This simplification is crucial because it presents the fraction in its most concise and manageable form. It allows for easier calculations and a clearer understanding of the relationship between the numerator and the denominator.
III. Decimal Representation: Expressing the Fraction as a Decimal
While simplifying to a whole number is ideal, it's beneficial to understand the decimal representation of the fraction. This is achieved by performing the division indicated by the fraction.
- Performing the Division: 75 ÷ 25 = 3.0
The decimal representation of 75/25 is 3.0, confirming the whole number simplification. This decimal form is particularly useful when working with calculations involving decimals or when representing the fraction in contexts requiring a decimal format.
IV. Percentage Equivalence: Converting the Fraction to a Percentage
Converting the fraction to a percentage provides another perspective on its value. Percentages are commonly used to represent proportions and ratios in everyday life.
-
Conversion Process: To convert a fraction to a percentage, we multiply the fraction by 100%.
(75/25) x 100% = 3 x 100% = 300%
This means that 75/25 represents 300%. This high percentage indicates that the numerator (75) is three times larger than the denominator (25).
V. Applications of 75/25 in Real-World Scenarios
Understanding 75/25 goes beyond simple arithmetic; it has practical applications in various real-world situations. Consider these examples:
-
Financial Calculations: Imagine you have invested $25 and earned a profit of $75. The ratio of profit to investment is 75/25, which simplifies to 3. This means you've tripled your initial investment.
-
Proportional Reasoning: If a recipe calls for 25 grams of flour and you want to triple the recipe, you would need 75 grams of flour (75/25 = 3 times the original amount).
-
Geometric Problems: If a rectangle has a width of 25 units and an area of 75 square units, its length is 75/25 = 3 units.
-
Data Analysis: If a survey shows that 25 out of 75 respondents prefer a certain product, the ratio is 25/75, simplifying to 1/3. This indicates that one-third of respondents prefer the product.
VI. Exploring Related Fractions and Concepts
Understanding 75/25 lays the foundation for exploring related fractions and mathematical concepts. Let's explore some connected ideas:
-
Equivalent Fractions: Any fraction that simplifies to 3 is equivalent to 75/25. Examples include 6/2, 9/3, 12/4, and so on. Understanding equivalent fractions is crucial for performing arithmetic operations and solving equations.
-
Improper Fractions and Mixed Numbers: While 75/25 simplifies to a whole number, it's important to remember that fractions where the numerator is larger than the denominator (improper fractions) can be expressed as mixed numbers (a whole number and a fraction). For instance, 100/25 is an improper fraction that simplifies to 4, representing 4 whole units.
VII. Expanding on the Concept of Ratios and Proportions
The fraction 75/25 is fundamentally a ratio – a comparison of two quantities. Understanding ratios is critical for various mathematical applications. A ratio can be expressed in various ways:
- Fraction: 75/25
- Colon Notation: 75:25
- "To" Notation: 75 to 25
Ratios are closely related to proportions, which state that two ratios are equal. Proportions are invaluable tools for solving problems involving scaling, similar figures, and various real-world applications. For instance, if the ratio of boys to girls in a class is 75:25 (or 3:1), and there are 100 students in total, we can use a proportion to determine the number of boys and girls individually.
VIII. Advanced Applications and Mathematical Connections
The simple fraction 75/25 opens doors to more complex mathematical ideas:
-
Algebra: The fraction can be incorporated into algebraic equations. For example, solving the equation x/25 = 3 would yield x = 75.
-
Calculus: While not directly applicable in basic calculus, the concept of limits and derivatives can be illustrated using sequences of fractions approaching the value of 75/25 (or 3).
-
Statistics and Probability: The fraction could represent probabilities or proportions in statistical analyses. For instance, if there's a 75% chance of success and a 25% chance of failure, the ratio of success to failure is 75/25, which simplifies to 3:1.
IX. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 75/25?
A: The simplest form is 3.
-
Q: How do you convert 75/25 to a decimal?
A: Divide 75 by 25, which results in 3.0.
-
Q: How do you convert 75/25 to a percentage?
A: Multiply 75/25 by 100%, which results in 300%.
-
Q: What are some real-world examples of using 75/25?
A: See Section V for examples in finance, recipes, geometry, and data analysis.
-
Q: Can 75/25 be expressed as a mixed number?
A: No, because it simplifies to a whole number (3). Mixed numbers are used for improper fractions where the numerator is greater than the denominator.
X. Conclusion: The Significance of Understanding 75/25
The fraction 75/25, seemingly straightforward, offers a gateway to understanding fundamental mathematical concepts. From simplification and decimal representation to percentage equivalence and real-world applications, its exploration provides a solid foundation in fractions, ratios, proportions, and their relevance in various fields. Mastering the manipulation and interpretation of such fractions is crucial for building a strong mathematical foundation and confidently approaching more complex mathematical challenges. The seemingly simple 75/25 acts as a microcosm of broader mathematical principles, illustrating the power of simplification, the diverse representation of quantities, and the practical applicability of mathematical concepts in our everyday lives.
Latest Posts
Latest Posts
-
80kh In Stone
Sep 10, 2025
-
70 Of 15
Sep 10, 2025
-
Physician Office Lab
Sep 10, 2025
-
5 X 2
Sep 10, 2025
-
53 5kg In Stone
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.