10000 X 100
stanleys
Sep 16, 2025 · 5 min read
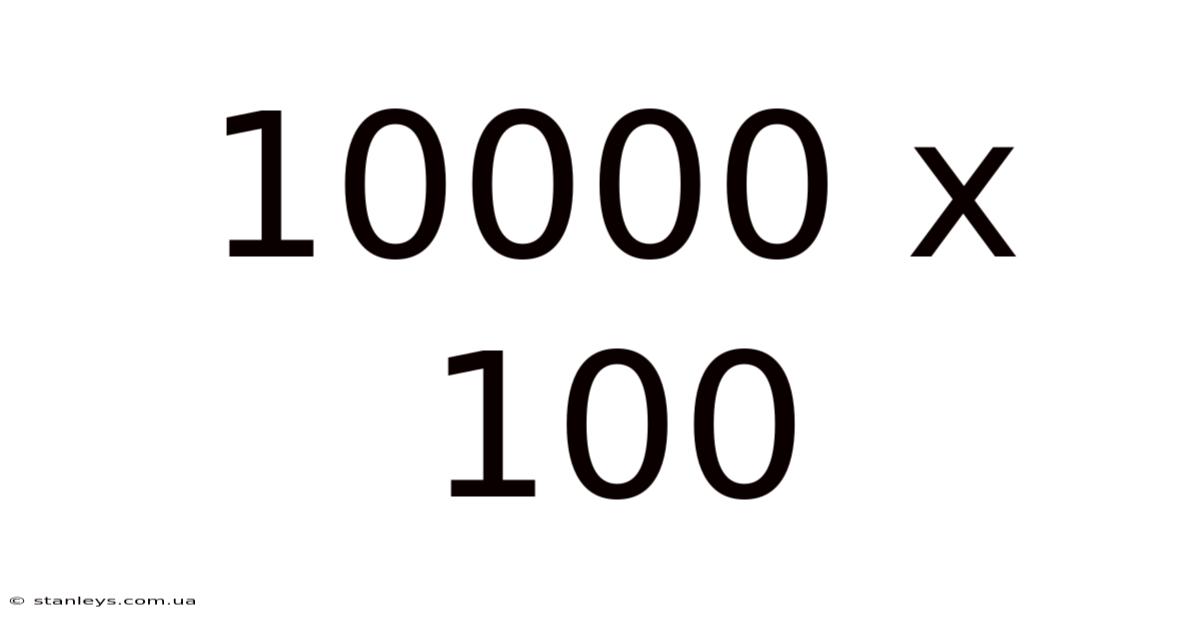
Table of Contents
Decoding 10,000 x 100: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 10,000 multiplied by 100, delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and broader implications of this type of multiplication. Understanding this seemingly basic calculation provides a strong foundation for grasping more complex mathematical concepts and real-world problem-solving. We'll explore different methods for solving this problem, discuss its relevance in various fields, and even touch upon some interesting historical context.
Understanding the Fundamentals: Multiplication and its Properties
Before diving into 10,000 x 100, let's refresh our understanding of multiplication. Multiplication is essentially repeated addition. For example, 3 x 4 means adding 3 four times (3 + 3 + 3 + 3 = 12). It's a fundamental arithmetic operation with several key properties:
- Commutative Property: The order of the numbers doesn't change the result (a x b = b x a). Therefore, 10,000 x 100 is the same as 100 x 10,000.
- Associative Property: When multiplying three or more numbers, you can group them in any way without affecting the result ((a x b) x c = a x (b x c)).
- Distributive Property: This property allows us to break down complex multiplications into simpler ones. For example, a x (b + c) = (a x b) + (a x c).
Calculating 10,000 x 100: Multiple Approaches
There are several ways to calculate 10,000 x 100. The simplest is using the basic multiplication method:
-
Standard Multiplication: We can perform the multiplication directly:
10000 x 100 -------- 00000 000000 1000000 -------- 1000000 -
Using Place Value: Understanding place value simplifies this calculation significantly. 10,000 has four zeros, and 100 has two zeros. Multiplying them together results in a number with six zeros (4 + 2 = 6 zeros). Therefore, 10,000 x 100 = 1,000,000 (one million).
-
Scientific Notation: Expressing the numbers in scientific notation provides another efficient way to solve this. 10,000 is 10<sup>4</sup> and 100 is 10<sup>2</sup>. Multiplying these gives 10<sup>4</sup> x 10<sup>2</sup> = 10<sup>(4+2)</sup> = 10<sup>6</sup> = 1,000,000.
-
Mental Math: With practice, you can perform this calculation mentally by focusing on the number of zeros.
Real-World Applications of Large-Scale Multiplication
The multiplication of large numbers like 10,000 x 100 is not just an abstract mathematical exercise; it has significant real-world applications across numerous fields:
-
Finance: Calculating large-scale investments, compound interest, or total revenue from a large number of transactions. Imagine a company selling 10,000 units of a product at $100 each – the total revenue is easily calculated using this multiplication.
-
Engineering and Construction: Estimating material requirements for large-scale projects. For example, calculating the total number of bricks needed for a building project might involve multiplying the number of bricks per layer by the number of layers.
-
Data Science and Computing: Processing and analyzing vast amounts of data. Handling large datasets often involves performing millions or billions of calculations, where understanding the principles of multiplication at this scale is critical.
-
Population Studies and Demographics: Calculating population projections or analyzing population distribution within a region.
Exploring Extensions: Larger Numbers and More Complex Calculations
The calculation 10,000 x 100 provides a foundational understanding that can be extended to more complex calculations involving larger numbers and more variables. Consider these examples:
-
100,000 x 1,000: This extends the concept to even larger numbers. The process remains the same: count the zeros (5 + 3 = 8) and the answer is 100,000,000.
-
10,000 x 100.5: This introduces decimals. You can solve this by breaking it down: (10,000 x 100) + (10,000 x 0.5) = 1,000,000 + 5,000 = 1,005,000.
-
Calculations with Variables: The same principles apply when dealing with variables. For example, if 'x' represents 10,000, then 'x * 100' would still be solved by adding the zeros or using scientific notation.
Historical Context: The Evolution of Multiplication Techniques
The understanding and application of multiplication have evolved over centuries. Early civilizations used various methods, including:
-
Ancient Egyptian Multiplication: They employed a doubling method to simplify calculations.
-
Babylonian Multiplication: They used a sexagesimal (base-60) system, which influenced our current measurement systems.
-
Ancient Greek Multiplication: They developed sophisticated geometric methods for multiplication.
The development of these methods and the advancement of our number systems (including the adoption of the decimal system) significantly simplified large-scale multiplication calculations.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to multiply 10,000 by 100?
A: The easiest way is to add the number of zeros. 10,000 has four zeros, and 100 has two zeros. Adding them together (4 + 2 = 6) gives you six zeros, resulting in 1,000,000.
-
Q: How can I check my answer to 10,000 x 100?
A: You can use a calculator to verify your answer. Alternatively, you can work backward by dividing 1,000,000 by either 10,000 or 100 to see if you get the original numbers.
-
Q: What are some real-world scenarios where this type of multiplication is used?
A: Many real-world scenarios involve multiplying large numbers, including financial calculations (revenue, interest), engineering (material estimations), and data processing (handling large datasets).
-
Q: What if one of the numbers wasn't a multiple of 100?
A: If the numbers weren't multiples of 10, you would need to use the standard multiplication method or a calculator. However, you could still simplify the calculation by breaking down the numbers into easier-to-manage components. For example, you could use the distributive property if the numbers were close to multiples of 100.
Conclusion: Beyond the Calculation
The seemingly simple calculation of 10,000 x 100 opens a door to a deeper understanding of mathematical principles and their practical applications. From the fundamental properties of multiplication to its real-world relevance across various fields, this calculation serves as a stepping stone to mastering more complex mathematical concepts. By exploring different methods of solving this problem and considering its historical context, we can appreciate the elegance and power of mathematics in its ability to solve intricate problems in a straightforward manner. The ability to understand and perform these calculations effectively remains a vital skill in the modern world.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10000 X 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.