10 Of 800
stanleys
Sep 11, 2025 · 7 min read
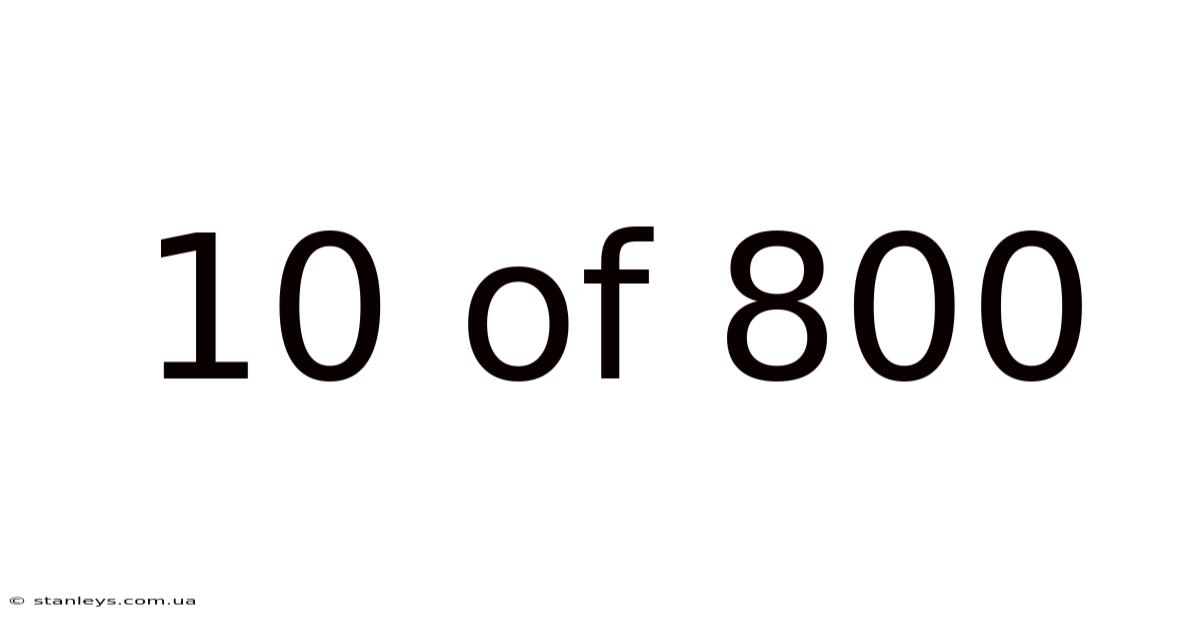
Table of Contents
Decoding the Enigma: A Deep Dive into the Fraction 10/800
The seemingly simple fraction 10/800 might appear insignificant at first glance. However, understanding its intricacies reveals a world of mathematical concepts, from basic simplification to advanced applications in various fields. This article will dissect 10/800, exploring its simplification, decimal representation, percentage equivalent, and real-world applications, providing a comprehensive understanding for readers of all mathematical backgrounds.
Introduction: Unveiling the Simplicity Within Complexity
The fraction 10/800, at its core, represents a ratio: 10 parts out of a total of 800 parts. This seemingly small ratio can be found in numerous situations, from calculating proportions in recipes to analyzing data in scientific experiments. Understanding how to manipulate and interpret this fraction is a crucial skill in mathematics and beyond. This guide aims to demystify 10/800, providing clear explanations and examples to enhance your mathematical proficiency. We will explore the process of simplification, conversion to decimals and percentages, and examine its implications within real-world contexts.
1. Simplifying the Fraction: Finding the Core Ratio
The first step in understanding 10/800 is simplifying it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (10) and the denominator (800). The GCD is the largest number that divides both 10 and 800 without leaving a remainder.
In this case, the GCD of 10 and 800 is 10. Dividing both the numerator and the denominator by 10, we get:
10 ÷ 10 = 1 800 ÷ 10 = 80
Therefore, the simplified form of 10/800 is 1/80. This simplified fraction represents the same ratio but is easier to work with in calculations and comparisons.
2. Decimal Representation: Expressing the Fraction as a Decimal
Converting the simplified fraction 1/80 to a decimal involves dividing the numerator (1) by the denominator (80). This can be done using long division or a calculator.
1 ÷ 80 = 0.0125
Therefore, the decimal representation of 10/800 (and its simplified form 1/80) is 0.0125. This decimal form is useful for calculations involving other decimal numbers and for visualizing the magnitude of the fraction.
3. Percentage Equivalent: Expressing the Fraction as a Percentage
To express the fraction 10/800 (or 1/80) as a percentage, we multiply the decimal representation (0.0125) by 100.
0.0125 x 100 = 1.25%
Therefore, 10/800 is equivalent to 1.25%. The percentage form is particularly useful for expressing proportions and comparisons, making it easier to understand the relative size of the fraction within a larger context.
4. Real-World Applications: Where 10/800 (or 1/80) Appears
The fraction 10/800, though seemingly small, appears in numerous real-world scenarios. Here are a few examples:
-
Surveys and Statistics: Imagine a survey of 800 people, where 10 respondents answered "yes" to a particular question. The fraction 10/800 (or 1.25%) represents the proportion of respondents who answered "yes." This data can be crucial for market research, opinion polls, and understanding public sentiment.
-
Manufacturing and Quality Control: In a manufacturing process, if 10 out of 800 products are defective, the fraction 10/800 (or 1.25%) represents the defect rate. This information is vital for identifying and addressing quality control issues.
-
Finance and Investments: If an investment of $800 yields a profit of $10, the fraction 10/800 (or 1.25%) represents the return on investment (ROI). Understanding ROI is critical for making informed financial decisions.
-
Scientific Experiments and Data Analysis: In scientific experiments, 10/800 might represent the proportion of successful trials out of a total of 800 trials. This data is essential for analyzing experimental results and drawing conclusions.
-
Recipe Scaling: If a recipe calls for 10 grams of an ingredient in a total mixture of 800 grams, the fraction 10/800 represents the proportion of that ingredient. This information is crucial for scaling recipes up or down.
5. Expanding the Understanding: Further Mathematical Explorations
Beyond its basic simplification and conversions, 10/800 can be used to illustrate several important mathematical concepts:
-
Ratios and Proportions: The fraction represents a specific ratio between two quantities. Understanding this ratio allows us to solve problems involving proportions, such as determining the number of defective items in a larger batch based on a sample size.
-
Percentages and Percentage Change: Converting the fraction to a percentage allows us to easily calculate percentage changes. For instance, if the number of defective items increases from 10 to 20 out of 800, we can calculate the percentage increase in the defect rate.
-
Fractional Arithmetic: We can perform various arithmetic operations with 10/800, such as addition, subtraction, multiplication, and division, using the rules of fraction arithmetic.
-
Decimal Arithmetic: Similarly, using the decimal representation (0.0125), we can perform decimal arithmetic operations, making it easier to integrate this fraction into calculations involving other decimal numbers.
6. Addressing Common Misconceptions:
A common misconception is that simplifying a fraction changes its value. This is incorrect. Simplifying a fraction merely expresses the same ratio in a more concise and manageable form. The values of 10/800 and 1/80 are identical; they represent the same proportion.
Another misconception revolves around the significance of small percentages. While 1.25% might seem insignificant on its own, in larger contexts, it can have a substantial impact. For example, a 1.25% defect rate in a large-scale manufacturing process could lead to significant losses.
7. Beyond the Basics: Advanced Applications
The fraction 10/800 can also be applied in more advanced mathematical contexts:
-
Probability and Statistics: The fraction could represent the probability of a certain event occurring. Understanding probability is crucial in various fields, including risk assessment, insurance, and game theory.
-
Calculus: Fractions are fundamental building blocks in calculus. Understanding how to manipulate fractions is essential for working with derivatives, integrals, and other calculus concepts.
-
Linear Algebra: Fractions can appear in matrices and vectors, which are used to model and solve systems of equations. This application is crucial in computer graphics, physics, and engineering.
8. FAQ: Addressing Frequently Asked Questions
-
Q: Is 10/800 the same as 1/80? A: Yes, they are equivalent fractions representing the same ratio.
-
Q: How do I convert 10/800 to a decimal? A: Divide the numerator (10) by the denominator (800) or the simplified fraction's numerator (1) by its denominator (80).
-
Q: How do I convert 10/800 to a percentage? A: Multiply the decimal equivalent by 100.
-
Q: What are some real-world examples of using 10/800? A: See Section 4 for numerous examples in various fields.
-
Q: Why is simplifying fractions important? A: Simplifying makes fractions easier to work with, compare, and understand.
9. Conclusion: The Power of a Simple Fraction
While initially appearing unassuming, the fraction 10/800 offers a rich exploration of mathematical concepts and practical applications. Understanding its simplification, decimal and percentage equivalents, and its relevance in real-world scenarios provides valuable insights into the power of ratios and proportions. This knowledge is not merely academic; it’s a fundamental skill applicable across various disciplines, highlighting the interconnectedness of seemingly disparate fields. Mastering the manipulation and interpretation of simple fractions like 10/800 builds a strong foundation for more advanced mathematical concepts and problem-solving. The seemingly simple fraction holds a surprising depth, emphasizing the importance of understanding basic mathematical principles to navigate a complex world.
10. Further Exploration: Expanding Your Mathematical Horizons
To further enhance your understanding, consider exploring related concepts such as:
-
Ratio and Proportion Problems: Practice solving problems involving ratios and proportions to solidify your understanding of how fractions represent relationships between quantities.
-
Percentage Calculations: Practice various percentage calculations, including percentage increase, percentage decrease, and calculating percentages of quantities.
-
Fraction Arithmetic: Practice adding, subtracting, multiplying, and dividing fractions to build proficiency in fraction manipulation.
By actively engaging with these related concepts, you will solidify your grasp of the mathematical principles underlying the seemingly simple fraction 10/800 and unlock its potential as a valuable tool in various quantitative applications.
Latest Posts
Latest Posts
-
56 5kg In Stones
Sep 11, 2025
-
Vegetables Onion Family
Sep 11, 2025
-
Vant Hoff Equation
Sep 11, 2025
-
15 Of 350
Sep 11, 2025
-
Rpm In Rad S
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 800 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.