10 Of 140
stanleys
Sep 10, 2025 · 7 min read
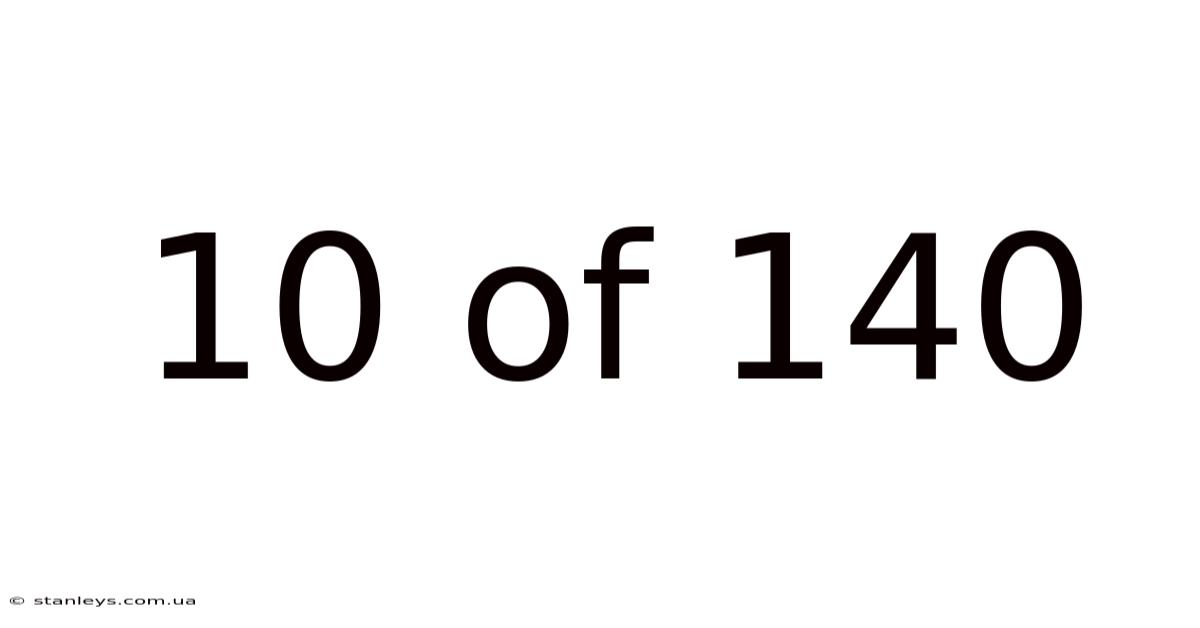
Table of Contents
Decoding the Enigma: Understanding 10 of 140 in the Context of Mathematical and Statistical Analysis
The phrase "10 of 140" might seem deceptively simple at first glance. However, its meaning and significance are highly dependent on the context in which it's presented. This seemingly innocuous numerical expression can represent a wide range of concepts, from simple fractions and proportions to more complex statistical analyses and probability calculations. This article will delve into various interpretations of "10 of 140," exploring its meaning across diverse mathematical and statistical domains. We'll examine how it's represented, its implications, and its application in real-world scenarios.
Understanding the Basic Representation: Fractions and Percentages
At its most fundamental level, "10 of 140" represents a fraction: 10/140. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10. This simplification yields the equivalent fraction 1/14. This simple fraction represents a portion or a part of a whole.
Converting this fraction to a percentage provides a more intuitive understanding. To do so, we divide the numerator (10) by the denominator (140) and multiply the result by 100: (10/140) * 100 ≈ 7.14%. Therefore, 10 out of 140 represents approximately 7.14% of the total. This percentage representation is particularly useful for comparing proportions and making relative comparisons across different datasets.
Expanding the Context: Proportions and Ratios
Beyond the basic fraction and percentage representations, "10 of 140" can also be understood within the context of proportions and ratios. A proportion is a statement of equality between two ratios. For example, we could express the proportion as:
10/140 = x/100
Solving for x gives us the percentage we calculated earlier (approximately 7.14). A ratio, on the other hand, simply compares two quantities. In this case, the ratio of 10 to 140 is 1:14, indicating that for every 14 items, there is 1 item of a specific type.
Understanding the context surrounding "10 of 140" is crucial. For instance, if we are discussing the success rate of a certain experiment, where 10 out of 140 trials were successful, then the 7.14% represents the success rate. If we are dealing with a survey, where 10 out of 140 respondents answered a specific way, then the percentage represents the proportion of respondents giving that particular response.
Statistical Significance and Hypothesis Testing
In the realm of statistics, "10 of 140" might represent a sample from a larger population. Consider a scenario where 140 individuals are randomly selected from a larger population, and 10 of them exhibit a specific characteristic. This data point could be used in various statistical analyses, such as hypothesis testing.
Hypothesis testing involves evaluating evidence to determine whether a hypothesis about a population parameter is supported by the sample data. In this case, the hypothesis could be about the prevalence of the characteristic in the larger population. The sample proportion (10/140) would be compared to the hypothesized population proportion using statistical tests, such as a z-test or a chi-squared test, to determine the likelihood of observing the sample data if the hypothesis were true.
The p-value resulting from these tests indicates the probability of obtaining the observed results (or more extreme results) if the null hypothesis (the hypothesis being tested) is true. A low p-value (typically below 0.05) suggests that the observed sample proportion is statistically significant, meaning that the characteristic is likely more prevalent in the population than what is hypothesized under the null hypothesis. However, the statistical significance also depends on the sample size; larger samples generally provide more precise estimates and increase the chances of detecting statistically significant differences.
Confidence Intervals and Margin of Error
Another critical statistical concept associated with "10 of 140" is the confidence interval. A confidence interval provides a range of values within which the true population parameter is likely to fall, with a certain level of confidence. For instance, a 95% confidence interval for the proportion of individuals exhibiting the characteristic in the larger population might be calculated based on the sample data (10/140).
The margin of error is an important component of the confidence interval, representing the uncertainty associated with the sample estimate. A larger sample size generally leads to a smaller margin of error and a narrower confidence interval, providing a more precise estimate of the population parameter. Conversely, a smaller sample size, such as the one represented by "10 of 140," might result in a wider confidence interval and a larger margin of error, indicating higher uncertainty in the estimation.
Bayesian Inference and Prior Probabilities
In the context of Bayesian inference, "10 of 140" can be incorporated into the calculation of posterior probabilities. Bayesian inference updates prior beliefs about a hypothesis based on new evidence. The prior probability represents the initial belief about the hypothesis before considering the new data, while the likelihood represents the probability of observing the data given the hypothesis. The posterior probability combines the prior and likelihood to provide an updated belief about the hypothesis after considering the new data.
The observed data (10 of 140) would be used to update the prior probability, leading to a posterior probability that reflects the updated belief about the hypothesis based on the sample evidence. The Bayesian approach allows for the incorporation of prior knowledge or expert opinions, which can be particularly useful when dealing with limited sample data, as in the case of "10 of 140."
Applications in Various Fields
The interpretation and significance of "10 of 140" vary considerably depending on the context of its application. Let's explore a few examples:
- Quality Control: In manufacturing, 10 out of 140 defective items might signify a 7.14% defect rate. This information helps assess the quality of the production process and identify potential areas for improvement.
- Medical Research: In a clinical trial, 10 out of 140 patients responding positively to a new treatment could suggest a low efficacy rate. Further investigation would be necessary to determine the treatment's effectiveness.
- Market Research: In a customer survey, 10 out of 140 respondents expressing dissatisfaction might indicate a need to address customer concerns and improve product or service quality.
- Environmental Science: 10 out of 140 sampled water sources testing positive for contamination represents a concerning percentage, potentially necessitating further investigation and remediation efforts.
Frequently Asked Questions (FAQ)
Q: How can I calculate the confidence interval for "10 of 140"?
A: Calculating a confidence interval requires specific statistical software or a statistical calculator. The process involves determining the sample proportion (10/140), the sample size (140), and the desired confidence level (e.g., 95%). The calculation utilizes the normal approximation to the binomial distribution or more advanced methods, depending on the context and sample size.
Q: What if the sample size is much smaller, say 10 out of 10?
A: If the sample size is small, the normal approximation might not be accurate. Exact methods, such as the binomial distribution, should be used to calculate probabilities and confidence intervals.
Q: How does sample size affect the interpretation of "10 of 140"?
A: A larger sample size generally provides a more accurate representation of the population parameter. With a larger sample, the margin of error would be smaller, leading to a more precise estimate of the true proportion. A smaller sample, like "10 of 140," is subject to greater sampling variability.
Q: Can "10 of 140" be used in other mathematical contexts?
A: Yes, "10 of 140" can represent various mathematical concepts beyond fractions, percentages, and proportions. For example, it could be part of a larger mathematical equation or model. The precise interpretation and application depend entirely on the equation or model in question.
Conclusion
The seemingly simple expression "10 of 140" opens a window into the vast world of mathematical and statistical analysis. Its interpretation depends heavily on the context in which it's used. From basic calculations of fractions and percentages to complex statistical hypothesis testing and Bayesian inference, understanding the nuances of this expression allows us to extract meaningful insights from data and make informed decisions across diverse fields. The key takeaway is that numbers don't speak for themselves; context is king when interpreting their meaning and drawing relevant conclusions. Always consider the specific application and the limitations of the data when analyzing this type of numerical information. Remember to consult with statistical experts if you need to perform advanced analysis or draw strong conclusions based on your data.
Latest Posts
Latest Posts
-
Mr Of Caco3
Sep 10, 2025
-
25 Of 280
Sep 10, 2025
-
Native American Patterns
Sep 10, 2025
-
115 Lbs Kg
Sep 10, 2025
-
Science S Words
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 140 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.