1/5 Of 35
stanleys
Sep 16, 2025 · 6 min read
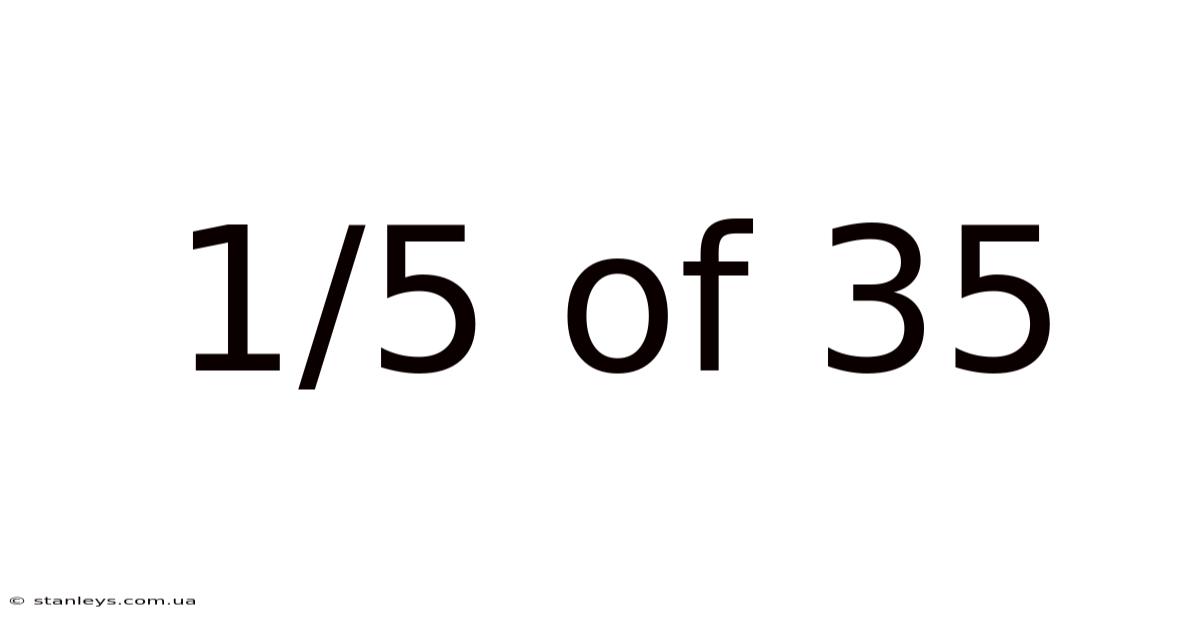
Table of Contents
Decoding 1/5 of 35: A Deep Dive into Fractions and Their Applications
This article explores the seemingly simple calculation of "1/5 of 35," delving far beyond the immediate answer to illuminate the underlying principles of fractions, their diverse applications, and their importance in various fields. Understanding this seemingly basic concept unlocks a gateway to more complex mathematical operations and real-world problem-solving. We'll cover the calculation itself, explore different methods of solving it, examine its relevance in various contexts, and address frequently asked questions.
Understanding Fractions: A Foundational Concept
Before tackling the specific problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 1/5, the denominator (5) means the whole is divided into five equal parts, and the numerator (1) signifies that we're considering one of those parts.
Calculating 1/5 of 35: Multiple Approaches
There are several ways to calculate 1/5 of 35. Let's explore the most common methods:
Method 1: Direct Multiplication
The most straightforward method is to multiply the fraction (1/5) by the whole number (35). This involves multiplying the numerator by the whole number and then dividing the result by the denominator:
(1/5) * 35 = (1 * 35) / 5 = 35 / 5 = 7
Therefore, 1/5 of 35 is 7.
Method 2: Finding the Fifth Part
Since we're looking for one-fifth of 35, we can simply divide 35 by 5:
35 / 5 = 7
This method directly addresses the meaning of the fraction, finding the size of one part when the whole is divided into five equal parts.
Method 3: Using Decimal Equivalents
We can convert the fraction 1/5 into its decimal equivalent by dividing the numerator by the denominator:
1 / 5 = 0.2
Then, multiply the decimal equivalent by 35:
0.2 * 35 = 7
This method is useful when working with calculators or when dealing with problems involving decimals.
Expanding the Concept: Fractions in Everyday Life
The calculation of "1/5 of 35" might seem trivial, but the concept of fractions is ubiquitous in our daily lives. Here are some examples:
- Cooking and Baking: Recipes often require fractional measurements of ingredients (e.g., 1/2 cup of sugar, 2/3 cup of flour). Understanding fractions is essential for accurate measurements and successful cooking.
- Shopping and Budgeting: Sales and discounts are frequently expressed as fractions (e.g., 1/3 off, 25% off, which is equivalent to 1/4 off). Understanding these fractions helps in making informed purchasing decisions and managing budgets effectively.
- Measurement and Engineering: Many fields, including engineering, construction, and design, rely heavily on fractional measurements for precision and accuracy.
- Data Analysis and Statistics: Fractions are fundamental in statistical analysis, allowing representation of proportions and probabilities. Understanding fractions helps interpret data accurately and draw meaningful conclusions.
- Time Management: We regularly use fractions to represent portions of time (e.g., a quarter of an hour, half a day). Effective time management often involves breaking down tasks into fractional parts.
Beyond the Basics: Exploring Related Concepts
Understanding 1/5 of 35 provides a springboard to explore more complex mathematical concepts:
- Equivalent Fractions: 1/5 is equivalent to other fractions, such as 2/10, 3/15, and so on. These fractions all represent the same proportion of the whole. Understanding equivalent fractions helps in simplifying calculations and comparing proportions.
- Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than its denominator (e.g., 7/5). A mixed number combines a whole number and a fraction (e.g., 1 2/5). Knowing how to convert between improper fractions and mixed numbers is essential for solving more complex fraction problems.
- Operations with Fractions: Beyond simple multiplication, we can also add, subtract, and divide fractions. Mastering these operations is crucial for advanced mathematical problem-solving.
- Percentages: Percentages are closely related to fractions. For instance, 1/5 is equivalent to 20% (1/5 * 100%). Converting between fractions and percentages allows flexibility in expressing and calculating proportions.
- Ratios and Proportions: Fractions are the basis of ratios and proportions, which are used to compare quantities and solve problems involving scaling and scaling up or down.
Real-World Applications: Case Studies
Let's illustrate how the concept of fractions, exemplified by "1/5 of 35," plays a crucial role in various real-world scenarios:
Scenario 1: Sharing Resources
Imagine 35 toys need to be divided equally among 5 children. Each child receives 1/5 of the total toys, which is 7 toys (35 / 5 = 7).
Scenario 2: Discount Calculation
A store offers a 20% discount on a $35 item. Since 20% is equivalent to 1/5, the discount amount is 1/5 of $35, which is $7. The final price would be $35 - $7 = $28.
Scenario 3: Project Management
A project is divided into 5 equal phases. If one phase is completed, then 1/5 of the project is finished. If the total project time is 35 days, then each phase takes 7 days (35 / 5 = 7).
Scenario 4: Recipe Scaling
A recipe calls for 35 grams of flour, and you want to make only 1/5 of the recipe. You'll need 1/5 of 35 grams, which is 7 grams (35 / 5 = 7).
These examples demonstrate how seemingly simple fraction calculations are fundamental to solving a variety of real-world problems.
Frequently Asked Questions (FAQ)
Q1: What are some common mistakes people make when working with fractions?
- Incorrectly multiplying or dividing numerators and denominators: Remember, you multiply numerators with numerators and denominators with denominators.
- Forgetting to simplify fractions: Always simplify fractions to their lowest terms.
- Confusing numerators and denominators: Make sure you understand which number represents the part and which represents the whole.
Q2: How can I improve my understanding of fractions?
- Practice regularly: The more you practice, the better you'll become.
- Use visual aids: Diagrams and manipulatives can help visualize fractions and their relationships.
- Seek help when needed: Don't hesitate to ask a teacher, tutor, or friend for help if you're struggling.
Q3: Are there online resources that can help me learn more about fractions?
While I cannot provide external links, a simple online search for "fraction tutorials" or "fraction worksheets" will yield many helpful resources.
Conclusion: Mastering Fractions – A Lifelong Skill
This in-depth exploration of "1/5 of 35" has revealed that this seemingly simple calculation is a gateway to a much broader understanding of fractions, their applications, and their importance in diverse fields. From cooking to engineering, budgeting to data analysis, fractions are an indispensable tool for navigating the complexities of the real world. Mastering the concepts discussed here will not only improve your mathematical skills but also enhance your problem-solving abilities and critical thinking in many areas of life. The ability to confidently work with fractions is a valuable asset that extends far beyond the classroom. Continue practicing, explore different methods, and apply your knowledge in real-world situations to truly solidify your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Mgs Magnesium Sulfide
Sep 16, 2025
-
X 3x X
Sep 16, 2025
-
20 Of 70
Sep 16, 2025
-
Factors Of 68
Sep 16, 2025
-
66km In Miles
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1/5 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.