X 3x X
stanleys
Sep 16, 2025 · 6 min read
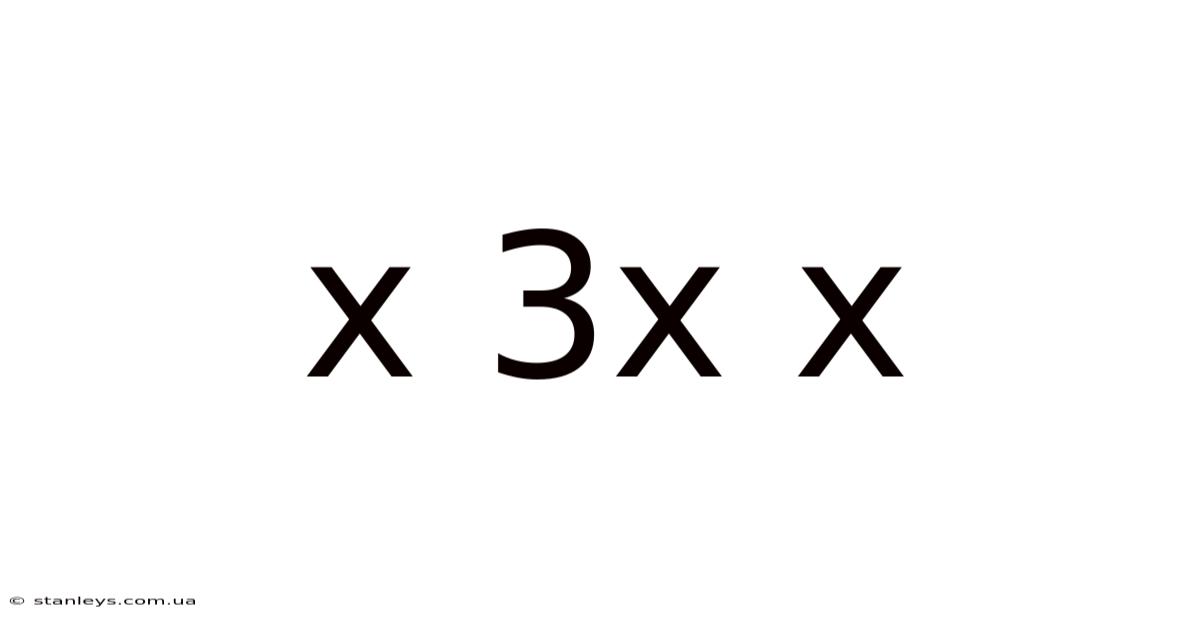
Table of Contents
Unraveling the Mystery of x³x: A Deep Dive into Cubic Functions and Beyond
The seemingly simple expression "x³x" initially presents a puzzle. Is it a typo? A cryptic code? Or something more profound? In reality, it opens a door to a fascinating exploration of cubic functions, their properties, applications, and the broader world of mathematics. This article delves into the intricacies of x³x, clarifying its meaning, exploring its mathematical significance, and uncovering its real-world applications. We'll unravel the mystery, step-by-step, making it accessible to everyone, regardless of their mathematical background.
Understanding the Basics: What Does x³x Mean?
At first glance, "x³x" might seem ambiguous. However, assuming it represents standard mathematical notation, it's interpreted as x³ * x, or x raised to the power of 3, multiplied by x. Using the rules of exponents, we can simplify this expression. Recall that x<sup>m</sup> * x<sup>n</sup> = x<sup>(m+n)</sup>. Therefore:
x³ * x = x<sup>(3+1)</sup> = x<sup>4</sup>
So, "x³x" simplifies to x⁴, or x raised to the power of 4. This seemingly small simplification opens up a world of possibilities in understanding and applying this function.
Exploring the Cubic Function (x³): A Foundation
Before delving deeper into x⁴, let's understand the underlying cubic function, x³. A cubic function is a polynomial function of degree 3, meaning the highest power of the variable x is 3. The general form of a cubic function is:
f(x) = ax³ + bx² + cx + d
where a, b, c, and d are constants, and a ≠ 0. The coefficient 'a' significantly impacts the function's shape and behavior. A positive 'a' results in a graph that rises to the right and falls to the left, while a negative 'a' produces the opposite behavior.
Key Characteristics of Cubic Functions:
- One or three real roots: A cubic function always has at least one real root (where the graph intersects the x-axis). It can have up to three distinct real roots.
- One or two turning points: Cubic functions can have one or two turning points (local maxima or minima), where the graph changes direction.
- Odd function: If b = c = d = 0, the function becomes f(x) = ax³, which is an odd function, meaning f(-x) = -f(x). Its graph is symmetric about the origin.
- Continuous and smooth: Cubic functions are continuous and smooth, meaning there are no breaks or sharp corners in their graph.
Delving into x⁴: The Quartic Function
Now, let's focus on x⁴, the result of simplifying x³x. This is a quartic function, a polynomial function of degree 4. Its general form is:
f(x) = ax⁴ + bx³ + cx² + dx + e
where a, b, c, d, and e are constants, and a ≠ 0.
Key Characteristics of Quartic Functions:
- Zero to four real roots: A quartic function can have zero, one, two, three, or four real roots.
- Zero to three turning points: A quartic function can have zero, one, two, or three turning points.
- Even function: If b = c = d = e = 0, the function becomes f(x) = ax⁴, which is an even function, meaning f(-x) = f(x). Its graph is symmetric about the y-axis.
- Continuous and smooth: Similar to cubic functions, quartic functions are continuous and smooth.
The graph of x⁴ differs significantly from x³. While x³ has rotational symmetry about the origin, x⁴ is symmetric about the y-axis. x⁴ also approaches infinity much faster as x increases compared to x³. This difference in behavior translates to distinct applications in various fields.
Real-World Applications of Cubic and Quartic Functions
Both cubic and quartic functions find numerous applications in diverse fields:
- Engineering: Cubic and quartic equations are crucial in solving problems related to structural analysis, fluid dynamics, and electrical engineering. For example, cubic splines are used in computer-aided design (CAD) to create smooth curves.
- Physics: Cubic and quartic equations often emerge in modeling physical phenomena, such as projectile motion, oscillations, and wave propagation.
- Economics: Cubic and quartic functions are used in economic modeling, particularly in production functions and cost-benefit analysis. They can help represent complex relationships between variables.
- Computer Graphics: Cubic and quartic curves and surfaces play a vital role in computer graphics, enabling the creation of realistic and smooth shapes in 3D modeling and animation. Bézier curves, frequently used in computer graphics, are based on cubic polynomials.
- Chemistry: Cubic equations can be used to solve for concentrations in chemical equilibrium calculations.
- Medicine: Mathematical models involving cubic and quartic functions may be used to describe the growth or decay of biological entities.
Graphical Representation and Analysis
Understanding the graphs of x³ and x⁴ is crucial for comprehending their behavior. Both functions can be plotted using graphing calculators or software. The graph of x³ shows a single inflection point at x = 0, whereas the graph of x⁴ has a single minimum point at x = 0. Analyzing these graphs allows us to visualize the range, domain, and other properties of the functions.
Step-by-Step Numerical Example
Let's illustrate with a numerical example:
Suppose we want to evaluate x³x for x = 2.
- Substitute: Replace x with 2 in the expression x³x: 2³ * 2
- Calculate the cube: 2³ = 2 * 2 * 2 = 8
- Multiply: 8 * 2 = 16
- Result: x³x = 16 when x = 2.
This simple example showcases the direct application of the function.
Frequently Asked Questions (FAQ)
Q1: What is the difference between x³ and x⁴?
A1: x³ is a cubic function, while x⁴ is a quartic function. They differ in their degree (3 and 4, respectively), which affects their shape, the number of potential real roots, and their behavior as x approaches infinity. x³ has rotational symmetry, while x⁴ has symmetry about the y-axis.
Q2: Can x³x be simplified further than x⁴?
A2: Yes, x³x simplifies to x⁴, which is the simplest form using standard algebraic notation.
Q3: Are there any other ways to interpret "x³x"?
A3: Without further context, the most logical interpretation is x³ * x. However, in specialized mathematical notations or programming languages, it might have alternative meanings. Always consider the context in which the expression is used.
Q4: How do I find the roots of x⁴?
A4: The roots of x⁴ are the values of x for which x⁴ = 0. In this case, the only real root is x = 0.
Q5: What are the applications of x⁴ in real-world problems?
A5: The function x⁴, as a special case of a quartic function, finds applications in various areas where modeling phenomena involving fourth-power relationships is necessary. These could include specific types of physical processes or economic models.
Conclusion: Beyond the Simple Expression
The initial enigma of "x³x" unveils a rich mathematical landscape. By simplifying it to x⁴, we opened the door to understanding quartic functions, their properties, and their significant applications across multiple disciplines. This exploration highlights the power of seemingly simple mathematical expressions to reveal complex relationships and their relevance to the world around us. While seemingly straightforward, delving into the details reveals the intricate beauty and practical utility of this powerful mathematical concept. The journey from x³x to x⁴ represents a stepping stone into a broader understanding of polynomial functions and their role in modeling and solving real-world problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3x X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.