1/4 Of 32
stanleys
Sep 09, 2025 · 6 min read
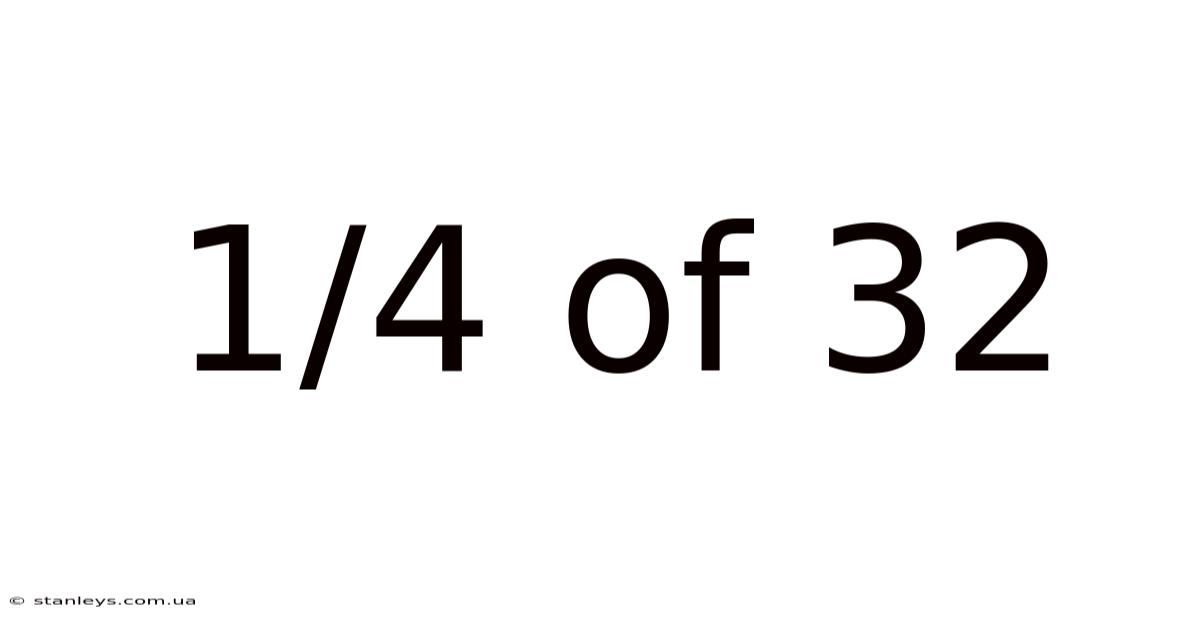
Table of Contents
Unveiling the Mystery: A Deep Dive into 1/4 of 32
Finding one-quarter of a number might seem like a simple arithmetic problem, suitable only for elementary school students. But the seemingly straightforward calculation of "1/4 of 32" opens a door to a world of mathematical concepts, practical applications, and even some surprising connections to other fields. This article will go beyond the simple answer, exploring the various ways to solve this problem, delving into the underlying mathematical principles, and examining its relevance in everyday life and beyond. Understanding fractions, percentages, and their applications is crucial for anyone navigating the quantitative aspects of the modern world. This exploration will benefit students, professionals, and anyone curious about the beauty and utility of mathematics.
Understanding Fractions: The Building Blocks
Before we tackle 1/4 of 32, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our case, 1/4 signifies one part out of four equal parts.
Methods for Calculating 1/4 of 32
There are several ways to calculate one-quarter of 32. Each method offers a unique perspective and reinforces different mathematical concepts.
1. Direct Division: The most straightforward approach involves dividing 32 by 4. This directly translates the fraction 1/4 into a division problem: 32 ÷ 4 = 8. This method highlights the core relationship between fractions and division. The denominator (4) tells us how many equal parts to divide the whole (32) into, and the numerator (1) indicates how many of those parts we are interested in.
2. Using Multiplication: We can also solve this using multiplication. Recall that finding a fraction of a number is equivalent to multiplying the number by the fraction. Therefore, 1/4 of 32 can be calculated as (1/4) * 32. To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same: (1 * 32) / 4 = 32/4. Then, we simplify the resulting fraction by dividing the numerator by the denominator: 32 ÷ 4 = 8. This method demonstrates the equivalence between fraction multiplication and division.
3. Visual Representation: Imagine a pizza cut into four equal slices. The whole pizza represents 32. Each slice represents 1/4 of the pizza. To find 1/4 of 32, we simply determine the size of one slice. Since the whole pizza (32) is divided into four equal slices, each slice represents 32 ÷ 4 = 8. This visual method provides an intuitive understanding of fractions and their practical applications.
Extending the Concept: Percentages and Ratios
The problem of finding 1/4 of 32 is intrinsically linked to percentages and ratios.
Percentages: One-quarter is equivalent to 25%. Therefore, finding 1/4 of 32 is the same as finding 25% of 32. To calculate this, we can use the formula: (Percentage/100) * Number. So, (25/100) * 32 = 0.25 * 32 = 8. This highlights the relationship between fractions and percentages, showing how they can be used interchangeably to represent parts of a whole.
Ratios: The problem can also be expressed as a ratio. The ratio of one part to four equal parts can be written as 1:4. To find the value of one part when the total is 32, we can set up a proportion: 1/4 = x/32. Solving for x (by cross-multiplication), we get 4x = 32, and therefore x = 8. This demonstrates how ratios can be used to solve problems involving proportional relationships.
Real-World Applications: Where 1/4 of 32 Matters
The seemingly simple calculation of 1/4 of 32 has surprisingly widespread applications in various fields:
-
Finance: Calculating interest rates, discounts, or profit shares often involves fractions. For example, a 25% discount on a $32 item would be equivalent to finding 1/4 of 32, resulting in an $8 discount.
-
Cooking and Baking: Recipes frequently require fractions of ingredients. If a recipe calls for 1/4 cup of sugar and you're making a double batch, you would need to calculate 1/4 of the doubled amount of sugar.
-
Construction and Engineering: Dividing materials, measuring distances, and calculating proportions are all crucial in these fields, often involving fractions and percentages.
-
Data Analysis: Interpreting data often involves calculating percentages and proportions, directly relating to fraction concepts. For instance, determining the percentage of a sample group exhibiting a specific trait relies on calculating fractions.
-
Everyday Life: From splitting bills equally among four people to calculating the portion of a pizza you'll eat, fraction understanding is essential for navigating daily situations.
Beyond the Basics: Exploring Further Mathematical Concepts
The simple problem of "1/4 of 32" can serve as a gateway to more advanced mathematical concepts:
-
Decimal Representation: 1/4 can also be expressed as a decimal: 0.25. Multiplying 0.25 by 32 also yields 8, demonstrating the interoperability of fractions and decimals.
-
Algebra: The concept can be generalized algebraically. Let 'x' represent a number. Then, finding 1/4 of 'x' is represented by (1/4)x or 0.25x.
-
Advanced Calculus: Understanding fractions forms the foundation for more advanced mathematical concepts like derivatives and integrals, crucial in fields like physics and engineering.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve 1/4 of 32? A: Absolutely! Most calculators can handle fraction calculations directly, or you can use the decimal equivalent (0.25) and multiply by 32.
-
Q: What if the fraction wasn't 1/4 but a different fraction, say 3/8? A: The same principles apply. You would multiply the whole number (32) by the fraction (3/8), resulting in (3 * 32) / 8 = 12.
-
Q: Are there any other ways to visually represent 1/4 of 32? A: Yes! You could use a bar graph, a pie chart, or even a collection of objects to illustrate the concept of dividing a whole into four equal parts.
Conclusion: The Enduring Importance of Fractions
While the calculation of "1/4 of 32" may appear trivial at first glance, its significance extends far beyond a simple arithmetic problem. This seemingly basic calculation underpins a vast array of mathematical concepts and practical applications. From the foundational understanding of fractions and percentages to their application in finance, cooking, engineering, and data analysis, the ability to grasp and manipulate fractions is an indispensable skill for navigating the world around us. By understanding the different methods of solving this problem and exploring its deeper implications, we not only gain a numerical answer but also a deeper appreciation for the power and elegance of mathematics. The seemingly simple act of finding one-quarter of 32 illuminates the interconnectedness of mathematical ideas and their relevance in countless aspects of our lives. Mastering this fundamental concept builds a strong foundation for tackling more complex mathematical challenges and fosters a deeper understanding of the quantitative world.
Latest Posts
Latest Posts
-
36kmh To Mph
Sep 09, 2025
-
Molarity To Millimoles
Sep 09, 2025
-
20 Times 30
Sep 09, 2025
-
120 Of 80
Sep 09, 2025
-
120kmh To Mph
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.