120 Of 80
stanleys
Sep 09, 2025 · 5 min read
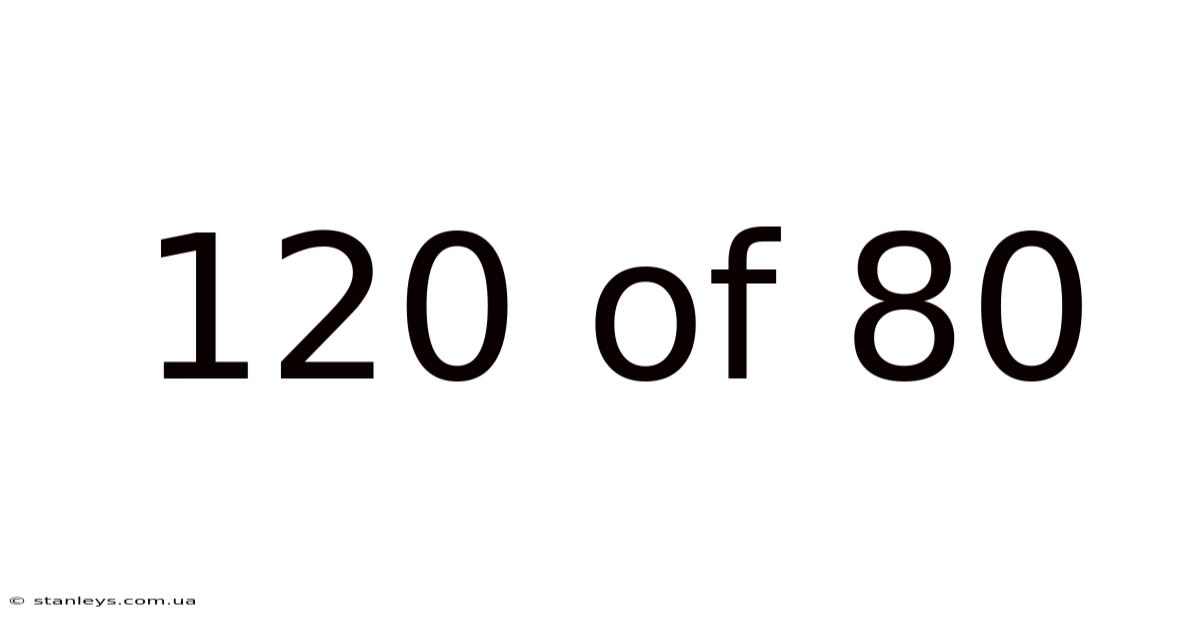
Table of Contents
Decoding the Math Mystery: Understanding 120% of 80
Understanding percentages is a fundamental skill in mathematics with far-reaching applications in everyday life, from calculating discounts and taxes to comprehending financial reports and statistical data. This article delves into the seemingly simple yet often misunderstood concept of finding a percentage greater than 100%, specifically focusing on how to calculate 120% of 80. We'll explore the calculation process, provide practical examples, and discuss the underlying mathematical principles to build a solid understanding. By the end, you’ll not only know the answer but also grasp the broader implications of percentage calculations.
Understanding Percentages: A Quick Refresher
Before diving into the specifics of 120% of 80, let's revisit the basic concept of percentages. A percentage is simply a fraction expressed as a part of 100. For instance, 50% represents 50/100, which simplifies to 1/2 or one-half. Similarly, 100% represents 100/100, or the whole amount. Percentages greater than 100% indicate an amount exceeding the original whole.
The key to understanding percentages lies in translating them into fractions or decimals for easier calculation. To convert a percentage to a decimal, simply divide the percentage by 100. For example, 120% becomes 120/100 = 1.2. This decimal representation is crucial for performing calculations.
Calculating 120% of 80: Step-by-Step Guide
Now, let's tackle the problem at hand: calculating 120% of 80. We can use two primary methods:
Method 1: Using the Decimal Equivalent
-
Convert the percentage to a decimal: As discussed, 120% is equal to 1.2.
-
Multiply the decimal by the original number: Multiply 1.2 by 80: 1.2 * 80 = 96
Therefore, 120% of 80 is 96.
Method 2: Using the Fraction Equivalent
-
Convert the percentage to a fraction: 120% can be expressed as 120/100, which simplifies to 6/5.
-
Multiply the fraction by the original number: Multiply 6/5 by 80: (6/5) * 80 = (6 * 80) / 5 = 480 / 5 = 96
Again, we arrive at the same answer: 120% of 80 is 96.
Practical Applications and Real-World Examples
Understanding how to calculate 120% of a number has numerous practical applications in various fields:
-
Finance: Imagine you invested $80 and your investment grew by 120%. Your total return would be $96, representing the original investment plus the 120% growth. This is crucial for calculating profit or loss on investments.
-
Business: If a company's sales increased by 120% from the previous year, and last year's sales were $80,000, this year's sales would be $176,000 (80,000 + (1.2 * 80,000)). This calculation helps analyze business growth and performance.
-
Sales and Marketing: A store offering a 120% markup on an item costing $80 would sell it for $176 (80 + (1.2 * 80)). This calculation is essential for pricing strategies.
-
Science and Engineering: Percentage increases exceeding 100% are frequently encountered in scientific experiments involving growth rates, population studies, or chemical reactions.
Beyond the Calculation: Understanding the Concept of Growth
The calculation of 120% of 80 represents more than just a mathematical exercise; it embodies the concept of growth or increase. In this context, the 120% indicates that the original amount (80) has expanded by 20% of its own value. This is different from simply adding 20% to the original number, which would result in a different outcome. Understanding this distinction is critical when dealing with percentage increases in real-world scenarios.
Addressing Common Misconceptions
Several common mistakes can occur when calculating percentages:
-
Incorrect Decimal Conversion: Failure to correctly convert the percentage to a decimal (e.g., mistaking 120% for 0.12 instead of 1.2) leads to an inaccurate result.
-
Incorrect Multiplication: Simple arithmetic errors during the multiplication step can also result in an incorrect answer. Always double-check your calculations.
-
Confusing Percentage Increase with Addition: Remember that a 120% increase is not the same as simply adding 20% to the original number. It represents a 20% increase on top of the original 100%.
Extending the Concept: Calculating X% of Y
The method used to calculate 120% of 80 can be generalized to find X% of any number Y. The formula is:
(X/100) * Y
This formula provides a versatile tool for calculating various percentage problems. Simply substitute the desired percentage (X) and the original number (Y) to find the result.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage decrease instead of an increase?
A: For percentage decreases, you would subtract the percentage (as a decimal) from 1 before multiplying. For example, to find 20% less than 80, you would calculate (1 - 0.20) * 80 = 64.
Q: Can I use a calculator to perform these calculations?
A: Yes, calculators are a valuable tool for performing these calculations, particularly for more complex percentage problems.
Q: Why is understanding percentages important?
A: Percentages are essential for understanding and interpreting data in various fields, from finance and business to science and everyday life. It allows for accurate analysis and informed decision-making.
Q: What if the percentage is less than 100%?
A: The same principles apply. For example, to calculate 50% of 80, you would calculate 0.50 * 80 = 40. The result will be a smaller value than the original number.
Conclusion: Mastering Percentage Calculations
This article has comprehensively explored the calculation of 120% of 80, providing a step-by-step guide, practical examples, and insights into the underlying mathematical principles. By mastering this seemingly simple calculation, you gain a foundational understanding of percentages that extends far beyond this single problem. The ability to accurately calculate and interpret percentages is a valuable skill applicable across numerous disciplines, empowering you to make informed decisions and confidently tackle real-world challenges involving proportional relationships. Remember to practice regularly and apply these concepts in diverse situations to further solidify your understanding. Through consistent practice and application, you can build confidence and proficiency in tackling percentage problems of any complexity.
Latest Posts
Latest Posts
-
76f To Celsius
Sep 09, 2025
-
30 Of 80
Sep 09, 2025
-
35 Of 40
Sep 09, 2025
-
56km In Miles
Sep 09, 2025
-
225lb In Kg
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 120 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.