1/4 Divided 3
stanleys
Sep 17, 2025 · 6 min read
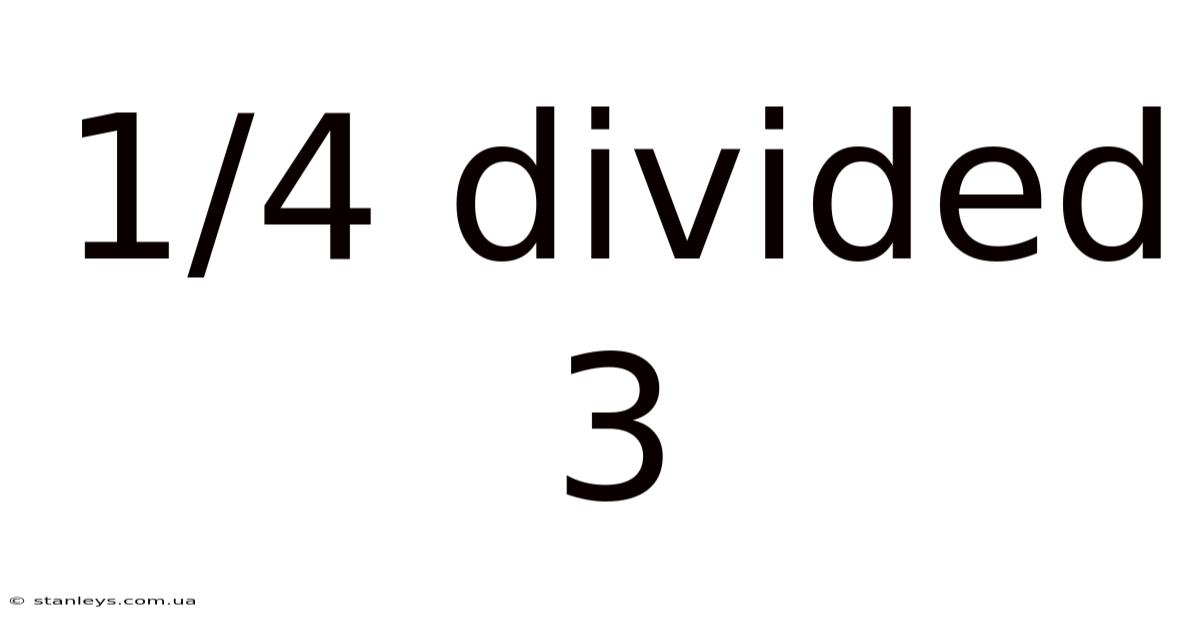
Table of Contents
Unpacking the Mystery: 1/4 Divided by 3
Understanding fractions can be a challenge, but mastering them opens doors to a wider world of mathematical possibilities. This article delves into the seemingly simple problem of 1/4 divided by 3, breaking down the process step-by-step, explaining the underlying principles, and exploring related concepts. We'll move beyond simply finding the answer to develop a deep understanding of fraction division. This will equip you to confidently tackle more complex fraction problems in the future.
Introduction: Why This Matters
Dividing fractions might seem daunting, but it's a fundamental skill in mathematics with practical applications in everyday life. From splitting recipes to calculating material needs for DIY projects, understanding fraction division is crucial. This seemingly simple problem, 1/4 divided by 3, provides an excellent platform to learn the core concepts. We'll unravel the mystery, exploring multiple approaches to ensure a thorough understanding.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common method for dividing fractions is the "keep, change, flip" method (also known as the reciprocal method). Let's apply it to our problem: 1/4 ÷ 3.
-
Keep: Keep the first fraction as it is: 1/4.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip the second fraction (or, more accurately, find its reciprocal). Since 3 can be written as 3/1, its reciprocal is 1/3.
Now our problem becomes: 1/4 × 1/3
To multiply fractions, simply multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 1) / (4 × 3) = 1/12
Therefore, 1/4 divided by 3 equals 1/12.
Visualizing the Division: A Real-World Analogy
Imagine you have a quarter of a pizza (1/4). You want to share this quarter equally among three people. How much pizza does each person get? This real-world scenario perfectly represents the problem 1/4 ÷ 3. To solve it visually, you would need to divide the quarter pizza into three equal slices. Each slice would represent 1/12 of the whole pizza. This visual representation reinforces the mathematical solution we obtained using the "keep, change, flip" method.
The Mathematical Explanation: Reciprocals and Multiplication
The "keep, change, flip" method isn't just a trick; it's based on sound mathematical principles. Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a number is simply 1 divided by that number. For example:
- The reciprocal of 3 is 1/3.
- The reciprocal of 5/2 is 2/5.
- The reciprocal of 1/4 is 4/1 (or simply 4).
By flipping the second fraction and changing the operation to multiplication, we're effectively applying the concept of reciprocals, transforming a division problem into a multiplication problem, which is generally easier to solve.
Solving Similar Problems: Expanding the Concept
Let's explore a few more examples to solidify our understanding:
-
Example 1: 2/5 ÷ 4
- Keep: 2/5
- Change: ×
- Flip: 1/4
- Multiply: (2 × 1) / (5 × 4) = 2/20 = 1/10
-
Example 2: 3/7 ÷ 2/3
- Keep: 3/7
- Change: ×
- Flip: 3/2
- Multiply: (3 × 3) / (7 × 2) = 9/14
-
Example 3: 1 ÷ 1/2
This example highlights that dividing by a fraction greater than 1 results in a larger number.
- Keep: 1 (or 1/1)
- Change: ×
- Flip: 2/1
- Multiply: (1 × 2) / (1 × 1) = 2
Dealing with Mixed Numbers: A Step-by-Step Approach
Mixed numbers (like 2 1/2) require an extra step before applying the "keep, change, flip" method. You need to convert them into improper fractions. An improper fraction has a numerator larger than its denominator.
Converting Mixed Numbers to Improper Fractions:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Keep the same denominator.
For example, to convert 2 1/2 to an improper fraction:
- (2 × 2) + 1 = 5
- Denominator remains 2.
- The improper fraction is 5/2.
Let's solve a problem involving mixed numbers:
-
Example 4: 1 1/2 ÷ 2/3
- Convert 1 1/2 to an improper fraction: (1 × 2) + 1 = 3/2
- Keep: 3/2
- Change: ×
- Flip: 3/2
- Multiply: (3 × 3) / (2 × 2) = 9/4 This can be converted back to a mixed number: 2 1/4
Beyond the Basics: Connecting Fraction Division to Other Concepts
Understanding fraction division helps solidify your grasp of several interconnected mathematical concepts:
-
Reciprocals: As discussed, the reciprocal is a key concept in fraction division. Understanding reciprocals is crucial for working with inverse functions and solving algebraic equations.
-
Proportionality: Fraction division is directly related to proportionality. When you divide a fraction, you're essentially finding a proportional part of the original fraction.
-
Ratio and Rates: Many real-world problems involve ratios and rates, which frequently require fraction division to solve.
-
Decimals: Fractions and decimals are interchangeable. You can convert a fraction to a decimal (by dividing the numerator by the denominator) and vice-versa. This provides alternative methods for solving problems involving fractions and decimals.
Frequently Asked Questions (FAQ)
-
Q: Why does the "keep, change, flip" method work?
- A: It works because dividing by a number is equivalent to multiplying by its reciprocal. This method is a shortcut that efficiently applies this mathematical principle.
-
Q: What if I have a whole number divided by a fraction?
- A: Treat the whole number as a fraction with a denominator of 1. Then apply the "keep, change, flip" method.
-
Q: Can I use a calculator for fraction division?
- A: Yes, most calculators have functions to handle fraction division. However, understanding the underlying principles is crucial for solving problems without a calculator and for developing a deeper mathematical understanding.
-
Q: Why is it important to understand fraction division?
- A: Fraction division is fundamental to many areas of mathematics and has practical applications in various fields, including cooking, construction, and engineering. A strong grasp of fractions is essential for success in higher-level mathematics.
Conclusion: Mastering Fraction Division
Mastering fraction division, even simple problems like 1/4 ÷ 3, lays a strong foundation for more advanced mathematical concepts. By understanding the "keep, change, flip" method, visualizing the process, and exploring its mathematical underpinnings, you can move beyond memorization to true comprehension. Practice solving various fraction division problems, including those involving mixed numbers, to solidify your skills and build confidence in your mathematical abilities. Remember, understanding the 'why' behind the methods is as important as knowing the 'how'. The journey of learning mathematics is a continuous process of exploration and discovery. Embrace the challenge, and you'll be rewarded with a deeper understanding of the fascinating world of numbers.
Latest Posts
Latest Posts
-
Larkin Building Buffalo
Sep 17, 2025
-
70 Of 32
Sep 17, 2025
-
Decimal Of 5 9
Sep 17, 2025
-
Liter Water Weight
Sep 17, 2025
-
Best Nail Wraps
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Divided 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.