0.4 X 4
stanleys
Sep 15, 2025 · 6 min read
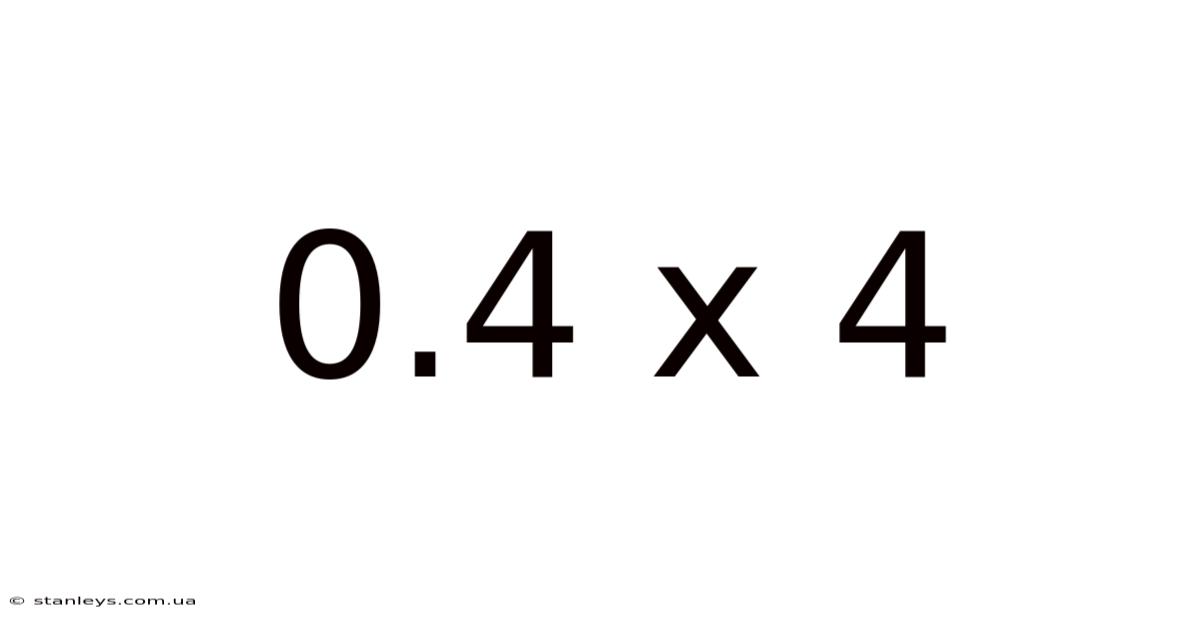
Table of Contents
Decoding 0.4 x 4: A Deep Dive into Decimal Multiplication
This article explores the seemingly simple calculation of 0.4 x 4, delving beyond the immediate answer to illuminate the underlying principles of decimal multiplication and its broader applications in mathematics, science, and everyday life. We'll examine different approaches to solving this problem, explaining the logic behind each method and highlighting the importance of understanding the concept of place value in the decimal system. Understanding decimal multiplication is crucial for mastering various mathematical concepts and tackling more complex problems.
Understanding Decimal Numbers
Before tackling the multiplication, let's refresh our understanding of decimal numbers. The decimal system, also known as the base-10 system, uses ten digits (0-9) to represent numbers. The position of a digit determines its value. For example, in the number 123.45, the digit 1 represents 100, the 2 represents 20, the 3 represents 3, the 4 represents 4 tenths (0.4), and the 5 represents 5 hundredths (0.05). This place value system is fundamental to understanding arithmetic operations with decimals.
Method 1: Direct Multiplication
The most straightforward method to solve 0.4 x 4 is to treat it like a standard multiplication problem, ignoring the decimal point initially.
-
Multiply the numbers without the decimal: 4 x 4 = 16
-
Count the decimal places: In the number 0.4, there is one decimal place.
-
Place the decimal point: Since there's one decimal place in the original number, place the decimal point in the answer one place from the right. This gives us the final answer: 1.6.
This method provides a quick and efficient way to solve the problem, particularly for simple decimal multiplications. However, understanding the underlying logic is crucial for tackling more complex problems.
Method 2: Fraction Conversion
Decimals can also be expressed as fractions. This alternative approach provides a deeper understanding of the mathematical operations involved.
-
Convert the decimal to a fraction: 0.4 is equivalent to 4/10.
-
Rewrite the multiplication problem: The problem becomes (4/10) x 4.
-
Multiply the numerators: 4 x 4 = 16
-
Keep the denominator: The denominator remains 10.
-
Simplify the fraction: The fraction 16/10 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This results in 8/5.
-
Convert the fraction back to a decimal: 8/5 can be converted to a decimal by dividing 8 by 5, which equals 1.6.
This method reinforces the connection between fractions and decimals, providing a solid foundation for understanding more advanced mathematical concepts.
Method 3: Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. While not the most efficient method for 0.4 x 4, applying the distributive property illustrates its versatility and can be useful for more complex calculations involving decimals.
We can rewrite 0.4 as 0.5 - 0.1. Therefore, 0.4 x 4 becomes (0.5 - 0.1) x 4. Applying the distributive property:
(0.5 - 0.1) x 4 = (0.5 x 4) - (0.1 x 4) = 2 - 0.4 = 1.6
This method demonstrates the flexibility of the distributive property and shows how it can break down a complex problem into simpler parts.
Visual Representation
Visual aids can enhance understanding, especially for those who benefit from a more concrete representation of abstract concepts. We can visualize 0.4 x 4 using area models. Imagine a rectangle with a width of 4 units and a height of 0.4 units. The area of this rectangle represents the product of 0.4 and 4. By dividing the rectangle into smaller squares, we can visually see that the total area is 1.6 square units.
Real-World Applications
The seemingly simple calculation of 0.4 x 4 finds numerous applications in diverse fields:
-
Finance: Calculating discounts, interest rates, or portions of a total amount. For example, a 40% (0.4) discount on a $4 item would be 0.4 x $4 = $1.60.
-
Science: In chemistry and physics, calculating concentrations, volumes, or other quantities often involves decimal multiplication.
-
Engineering: Scaling models, calculating material requirements, and determining dimensions often necessitate decimal calculations.
-
Everyday Life: Dividing a bill evenly among friends, calculating the cost of items based on unit price, and measuring quantities using decimal units (e.g., kilograms, meters, liters) all involve decimal multiplication.
Expanding the Concept: Multiplying Larger Decimals
The principles discussed above extend to more complex decimal multiplications. For example, consider 0.45 x 4.
-
Multiply without the decimal: 45 x 4 = 180
-
Count decimal places: There are two decimal places in 0.45.
-
Place the decimal point: Place the decimal point two places from the right, resulting in 1.80 or 1.8.
The same principles apply when multiplying decimals by other decimals. For instance, 0.4 x 0.2:
-
Multiply without the decimal: 4 x 2 = 8
-
Count decimal places: There are two decimal places in total (one in 0.4 and one in 0.2).
-
Place the decimal point: Place the decimal point two places from the right, resulting in 0.08.
Frequently Asked Questions (FAQ)
Q: What if I forget the rules for decimal multiplication?
A: The safest approach is to convert the decimals into fractions. Fractions make the multiplication process more transparent and reduce the risk of errors related to decimal placement.
Q: Are there other ways to solve 0.4 x 4?
A: Yes, you could use a calculator, but understanding the manual methods allows for a deeper comprehension of the underlying mathematical principles. Repeated addition (0.4 + 0.4 + 0.4 + 0.4) is another, albeit less efficient, approach.
Q: Why is understanding place value so important in decimal multiplication?
A: Place value dictates the magnitude of each digit in a number. Without a clear understanding of place value, you won't be able to correctly position the decimal point in your answer, leading to incorrect results.
Q: How can I improve my skills in decimal multiplication?
A: Practice is key. Start with simple problems like 0.4 x 4 and gradually move towards more complex ones. Focus on understanding the different methods and choosing the one that works best for you. Using various resources like online calculators, educational videos, and worksheets can also help reinforce your learning.
Conclusion
The seemingly straightforward calculation of 0.4 x 4 opens a window into the fascinating world of decimal multiplication. By exploring different methods, understanding the underlying principles of place value, and recognizing the real-world applications, we've moved beyond a simple answer to a deeper comprehension of the mathematical concepts involved. This knowledge empowers us to tackle more complex problems confidently and appreciate the practical relevance of decimal multiplication in various aspects of our lives. Mastering decimal multiplication is not just about getting the right answer; it's about developing a strong mathematical foundation that extends far beyond this single calculation.
Latest Posts
Latest Posts
-
Mmolar To Um
Sep 15, 2025
-
0 75 X 5
Sep 15, 2025
-
134lbs In Kg
Sep 15, 2025
-
96km In Miles
Sep 15, 2025
-
Feeding Past Tense
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 0.4 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.