X 7 2
stanleys
Sep 10, 2025 · 6 min read
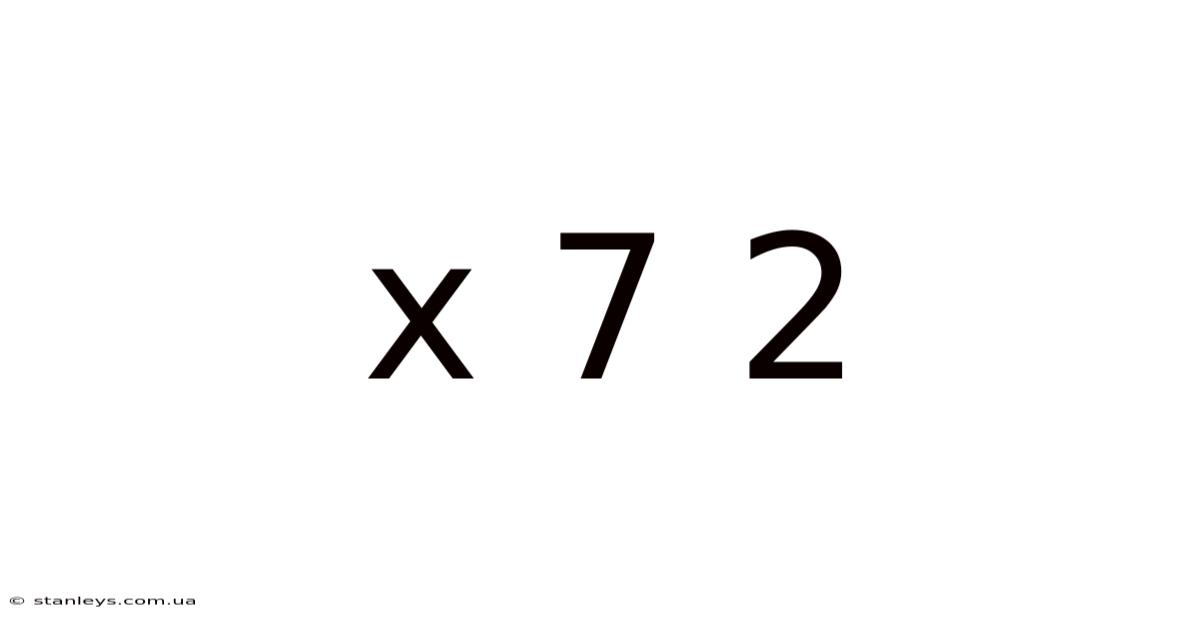
Table of Contents
Decoding the Mystery: Exploring the Mathematical Concept of x⁷²
The expression "x⁷²" might seem daunting at first glance, especially for those who haven't delved deeply into the world of algebra and exponents. However, understanding this seemingly complex concept is achievable with a methodical approach, breaking down the components and exploring their implications. This article will provide a comprehensive guide to understanding x⁷², covering its meaning, applications, and potential challenges in different mathematical contexts. We will explore the basics of exponents, delve into the properties of this specific expression, and even tackle some real-world applications. By the end, you'll not only understand what x⁷² means but also appreciate the power and elegance of mathematical notation.
Understanding the Fundamentals: Exponents and Their Properties
Before diving into the specifics of x⁷², it's crucial to establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example, in the expression 2³, the base is 2 and the exponent is 3. This means 2 multiplied by itself three times: 2 x 2 x 2 = 8.
Several key properties govern exponents:
-
Product of Powers: When multiplying two numbers with the same base, you add their exponents. For example, x² * x³ = x⁽²⁺³⁾ = x⁵.
-
Quotient of Powers: When dividing two numbers with the same base, you subtract their exponents. For example, x⁵ / x² = x⁽⁵⁻²⁾ = x³.
-
Power of a Power: When raising a power to another power, you multiply the exponents. For example, (x²)³ = x⁽²ˣ³⁾ = x⁶.
-
Power of a Product: When raising a product to a power, you raise each factor to that power. For example, (xy)² = x²y².
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and denominator to that power. For example, (x/y)² = x²/y².
-
Zero Exponent: Any non-zero number raised to the power of zero is equal to 1. For example, x⁰ = 1 (where x ≠ 0).
-
Negative Exponent: A negative exponent indicates a reciprocal. For example, x⁻² = 1/x².
These properties are fundamental to working with expressions like x⁷². Understanding them thoroughly will allow you to manipulate and simplify such expressions effectively.
Deconstructing x⁷²: What Does it Mean?
Now, let's focus on x⁷². This expression signifies the base x raised to the power of 72. In other words, it represents x multiplied by itself 72 times:
x * x * x * x * ... * x (72 times)
The value of x⁷² depends entirely on the value of x. If x is a number, the expression will result in a specific numerical value. However, if x represents a variable, the expression remains algebraic, representing a specific power of that variable.
Applications of x⁷² in Different Mathematical Contexts
The application of x⁷² varies significantly depending on the mathematical context. Let’s explore some examples:
-
Algebra: In algebra, x⁷² is a monomial—a single term consisting of a variable raised to a power. It can be used in polynomial expressions, equations, and inequalities. For instance, it might appear as part of a larger polynomial like 3x⁷² + 2x⁵ - 7x + 1. Understanding the properties of exponents is essential for simplifying, expanding, and factoring such polynomials.
-
Calculus: In calculus, x⁷² can be used in differentiation and integration problems. The power rule of differentiation states that the derivative of xⁿ is nxⁿ⁻¹. Therefore, the derivative of x⁷² would be 72x⁷¹. Similarly, the integral of xⁿ is (xⁿ⁺¹)/(n+1) + C, meaning the integral of x⁷² would be (x⁷³)/73 + C, where C is the constant of integration.
-
Number Theory: Within number theory, x⁷² might be investigated for its properties related to divisibility, prime factorization, and modular arithmetic. For instance, you might explore whether certain values of x result in x⁷² being a perfect square, a prime number, or having specific properties modulo a particular integer.
-
Computer Science: In computer science, especially in areas like cryptography and algorithm analysis, x⁷² could represent a large number, potentially relevant to computational complexity or the efficiency of an algorithm. The sheer size of the exponent highlights the importance of efficient computational methods for handling such expressions.
Challenges and Considerations When Working with x⁷²
While relatively straightforward conceptually, working with x⁷² presents certain practical challenges:
-
Computational Complexity: Calculating the numerical value of x⁷² for large values of x can be computationally intensive. Direct multiplication would be extremely inefficient. Specialized algorithms and computational tools are often necessary for handling such calculations efficiently.
-
Numerical Overflow: When dealing with extremely large values of x, calculating x⁷² may lead to numerical overflow, especially on computers with limited precision. The resulting number might exceed the capacity of the data type used to store it, leading to inaccurate results or errors.
-
Approximations: In certain cases, particularly when dealing with extremely large numbers or continuous functions, approximations may be necessary to simplify calculations involving x⁷². Techniques like Taylor series expansions can be employed to approximate the value of x⁷² under specific conditions.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between x⁷² and 72x?
A: x⁷² means x multiplied by itself 72 times, while 72x means 72 multiplied by x. These are fundamentally different operations.
-
Q: Can x⁷² ever be negative?
A: Whether x⁷² is negative or positive depends entirely on the value of x. If x is positive, then x⁷² will always be positive. If x is negative, the result will be positive if the exponent (72) is an even number, and negative if the exponent is odd. Since 72 is even, x⁷² will always be positive for any real number x (excluding zero).
-
Q: How do I simplify expressions involving x⁷²?
A: Simplification depends on the context. If you have an expression like x⁷² * x³, you can simplify using the product of powers rule: x⁷² * x³ = x⁷⁵. Similarly, applying the quotient of powers rule for division, and power of a power rule for nested exponents will be helpful in simplifying complex expressions.
-
Q: What are some real-world examples where x⁷² might be used?
A: While it’s uncommon to see x⁷² explicitly in real-world problems, the underlying concept of exponents is ubiquitous. Applications include compound interest calculations (where the exponent represents time), population growth models, radioactive decay, and various scientific simulations.
Conclusion: Mastering the Power of x⁷²
Understanding x⁷² goes beyond merely knowing its definition. It entails grasping the fundamental principles of exponents, their properties, and their applications across various mathematical fields. While the expression itself might initially seem complex, its components are relatively straightforward. By breaking down the problem into smaller, manageable parts, and by mastering the fundamental rules of exponents, you can effectively analyze, manipulate, and apply expressions like x⁷² in a wide range of mathematical contexts. This understanding lays a crucial foundation for more advanced mathematical concepts and problem-solving. The journey to mastering this seemingly complex expression is a testament to the beauty and power of mathematical logic and the systematic approach required to unlock its secrets. Remember to practice regularly to solidify your understanding and build confidence in tackling increasingly complex mathematical challenges.
Latest Posts
Latest Posts
-
Necesitamos In Spanish
Sep 10, 2025
-
30 Of 70
Sep 10, 2025
-
1500m To Miles
Sep 10, 2025
-
The Eight Kings
Sep 10, 2025
-
67inches In Cm
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X 7 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.