X 2 2x
stanleys
Sep 12, 2025 · 6 min read
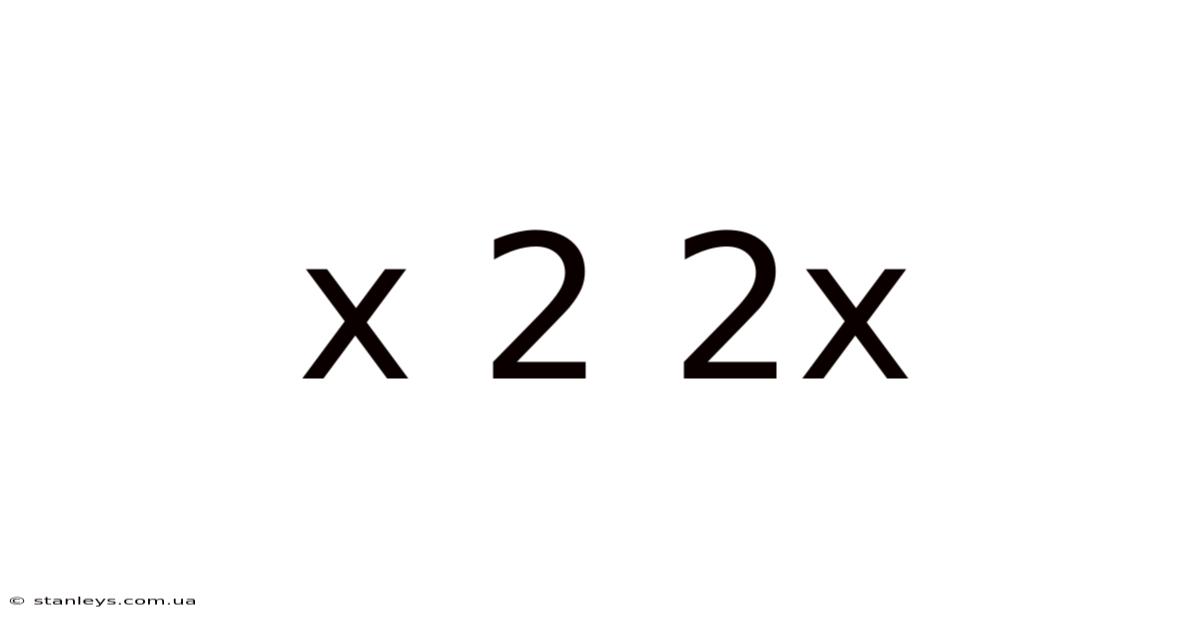
Table of Contents
Decoding the Mystery: A Deep Dive into the Expression "x² + 2x"
This article delves into the mathematical expression x² + 2x, exploring its various interpretations, applications, and significance in algebra and beyond. We'll unpack its meaning, explore methods for solving equations involving this expression, and delve into its practical applications in diverse fields. Understanding x² + 2x is fundamental to grasping many key concepts in mathematics, and this comprehensive guide will equip you with the knowledge and confidence to tackle it effectively.
Introduction: What Does x² + 2x Mean?
The expression x² + 2x represents a quadratic expression, a type of polynomial where the highest power of the variable (x) is 2. It's a foundational element in algebra, frequently appearing in equations, graphs, and real-world problem-solving. At its core, x² signifies 'x multiplied by x' (or x to the power of 2), while 2x represents '2 multiplied by x'. The '+' symbol indicates that these two terms are added together. Therefore, x² + 2x is the sum of a squared term and a linear term. Understanding this seemingly simple expression opens doors to a vast world of mathematical possibilities.
Understanding the Components:
Let's break down the individual components of x² + 2x to solidify our understanding:
-
x² (x squared): This term represents the area of a square with sides of length x. If x = 3, for example, x² = 9, representing the area of a 3x3 square. It's a quadratic term because the exponent is 2.
-
2x (two x): This term represents the area of two rectangles, each with one side of length x and the other side of length 1. Alternatively, if we consider x as a quantity, 2x represents twice that quantity. It's a linear term because the exponent is 1 (implied).
-
+ (plus): This symbol simply indicates addition; we are combining the areas (or quantities) represented by x² and 2x.
Methods for Solving Equations Involving x² + 2x:
The expression x² + 2x rarely stands alone; it typically appears within an equation that needs solving. The methods used depend on the form of the equation. Here are some common scenarios:
1. Solving x² + 2x = 0:
This is a relatively straightforward equation. We can factor out x:
x(x + 2) = 0
This equation is true if either x = 0 or (x + 2) = 0. Therefore, the solutions are x = 0 and x = -2.
2. Solving x² + 2x = c (where c is a constant):
This requires a more advanced technique. One approach is completing the square. Let's illustrate:
x² + 2x = c
To complete the square, we take half of the coefficient of x (which is 2), square it (resulting in 1), and add it to both sides:
x² + 2x + 1 = c + 1
This transforms the left side into a perfect square trinomial:
(x + 1)² = c + 1
Now, we can solve for x by taking the square root of both sides:
x + 1 = ±√(c + 1)
x = -1 ± √(c + 1)
This gives us two solutions for x, depending on the value of c.
3. Solving Quadratic Equations Using the Quadratic Formula:
For more complex equations of the form ax² + bx + c = 0, where a, b, and c are constants, the quadratic formula is invaluable:
x = [-b ± √(b² - 4ac)] / 2a
In our case (x² + 2x = 0 or x² + 2x - 0 = 0), a = 1, b = 2, and c = 0. Substituting these values into the quadratic formula confirms our earlier solutions (x = 0 and x = -2).
4. Graphical Representation:
The expression x² + 2x can be visually represented as a parabola. Plotting points corresponding to different x values and their corresponding y values (y = x² + 2x) will reveal a U-shaped curve. The x-intercepts of this parabola represent the solutions to the equation x² + 2x = 0 (which are x = 0 and x = -2). The vertex of the parabola represents the minimum value of the expression.
Applications of x² + 2x in Real-World Scenarios:
The seemingly abstract expression x² + 2x has surprisingly practical applications across diverse fields:
-
Physics: Equations of motion often involve quadratic expressions. For example, calculating the distance traveled by an object under constant acceleration might involve an equation with terms similar to x² + 2x.
-
Engineering: Designing structures, optimizing processes, and modeling various systems often necessitate solving quadratic equations, with x² + 2x potentially appearing as part of a larger equation.
-
Economics: Mathematical models used in economics, such as those dealing with profit maximization or cost minimization, frequently utilize quadratic functions.
-
Computer Science: Algorithms and simulations might employ quadratic equations to model various phenomena, solve optimization problems, or represent curved shapes in computer graphics.
-
Finance: Calculating compound interest or modeling investment growth might involve equations containing quadratic terms.
Further Exploration: Factoring and Completing the Square
Let's explore two crucial algebraic techniques related to manipulating x² + 2x:
Factoring: Factoring involves expressing a quadratic expression as the product of two linear expressions. In the case of x² + 2x, we factored it as x(x + 2), revealing the roots directly. Factoring is a powerful tool for simplifying expressions and solving equations.
Completing the Square: This technique transforms a quadratic expression into a perfect square trinomial, making it easier to solve or analyze. As shown earlier, completing the square for x² + 2x results in (x + 1)² - 1, which has a readily apparent vertex and can be used to solve related equations.
Frequently Asked Questions (FAQ):
-
Q: Is x² + 2x always positive?
- A: No. The expression can be positive, negative, or zero depending on the value of x. For example, if x = 1, x² + 2x = 3; if x = -3, x² + 2x = 3; and if x = 0 or x = -2, x² + 2x = 0.
-
Q: What is the vertex of the parabola represented by y = x² + 2x?
- A: The x-coordinate of the vertex is found using -b/2a (from the standard quadratic form ax² + bx + c), which is -2/2(1) = -1. The y-coordinate is found by substituting x = -1 into the equation: y = (-1)² + 2(-1) = -1. Therefore, the vertex is at (-1, -1).
-
Q: How do I find the roots of x² + 2x = 6?
- A: First, rearrange the equation to x² + 2x - 6 = 0. Then, you can use the quadratic formula with a = 1, b = 2, and c = -6 to find the roots.
-
Q: What is the difference between x² + 2x and (x + 2)²?
- A: (x+2)² expands to x² + 4x + 4. This is not the same as x² + 2x. They represent different quadratic expressions with different graphs and solutions.
Conclusion: Mastering x² + 2x and Beyond
The expression x² + 2x, while seemingly simple, forms a cornerstone of algebraic understanding. By grasping its components, mastering solution techniques like completing the square and the quadratic formula, and appreciating its real-world applications, you'll gain a profound understanding of quadratic expressions and their significance in mathematics and beyond. This exploration goes beyond simple equation solving; it's about building a solid foundation for more complex mathematical concepts and problem-solving skills. Continue practicing and exploring further to unlock the full potential of quadratic equations and the vast landscape of mathematical possibilities they represent.
Latest Posts
Latest Posts
-
Credit Investigation Department
Sep 12, 2025
-
32km In Miles
Sep 12, 2025
-
Victorian Era Cosmetics
Sep 12, 2025
-
Anti Bumping Granules
Sep 12, 2025
-
Cool Runnings Quotes
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.