Simplify 18 30
stanleys
Sep 16, 2025 · 6 min read
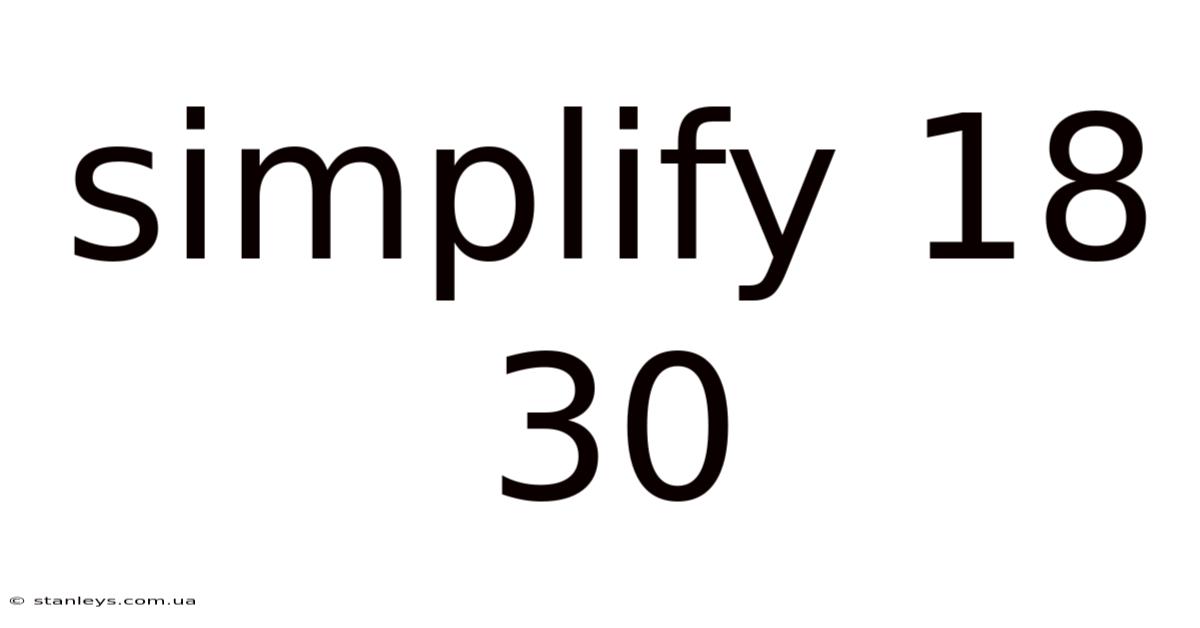
Table of Contents
Simplifying Fractions: A Deep Dive into 18/30
Understanding how to simplify fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This article will explore the process of simplifying fractions, using the example of 18/30, and will delve into the underlying mathematical principles. We’ll cover various methods, explain why simplification is important, and address frequently asked questions. By the end, you’ll not only know how to simplify 18/30 but also possess a solid understanding of fraction simplification applicable to any fraction.
Introduction: What Does it Mean to Simplify a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. In essence, we’re finding the simplest representation of the same fractional value. For instance, 18/30 represents the same portion of a whole as a simpler fraction we'll discover soon. This process is essential for clearer understanding and easier calculations.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient method for simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. Let's apply this to 18/30:
- Find the factors of 18: 1, 2, 3, 6, 9, 18
- Find the factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Identify the common factors: 1, 2, 3, 6
- Determine the greatest common factor (GCF): The largest common factor is 6.
Now, divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 30 ÷ 6 = 5
Therefore, the simplified form of 18/30 is 3/5.
Method 2: Prime Factorization
Prime factorization is another powerful technique for finding the GCD. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). Let's apply this method to 18/30:
-
Find the prime factorization of 18: 2 x 3 x 3 = 2 x 3²
-
Find the prime factorization of 30: 2 x 3 x 5
-
Identify common prime factors: Both 18 and 30 share a '2' and a '3'.
-
Calculate the GCD: The GCD is the product of the common prime factors: 2 x 3 = 6
-
Simplify the fraction: Divide both the numerator and denominator by the GCD (6): 18 ÷ 6 = 3 and 30 ÷ 6 = 5.
Again, the simplified fraction is 3/5. This method is particularly useful for larger numbers where finding all factors might be more challenging.
Method 3: Stepwise Simplification
If you don't immediately see the GCD, you can simplify the fraction step-by-step by dividing both the numerator and the denominator by any common factor you notice. You repeat this process until no more common factors exist. Let’s illustrate with 18/30:
-
Notice that both 18 and 30 are even numbers, so they are divisible by 2: 18 ÷ 2 = 9 30 ÷ 2 = 15 This gives us the fraction 9/15.
-
Now, observe that both 9 and 15 are divisible by 3: 9 ÷ 3 = 3 15 ÷ 3 = 5 This simplifies to 3/5.
Since 3 and 5 share no common factors other than 1, we've reached the simplest form. This method is intuitive and easy to follow, but it might take longer than the GCD method for larger fractions.
Why is Simplifying Fractions Important?
Simplifying fractions is more than just a mathematical exercise; it’s essential for several reasons:
-
Clarity: Simplified fractions are easier to understand and interpret. 3/5 is much clearer than 18/30.
-
Efficiency: Simplified fractions make calculations simpler and faster. Imagine adding 18/30 and 9/15; it’s much easier to add 3/5 + 3/5.
-
Accuracy: Working with simplified fractions reduces the risk of errors in calculations, especially when dealing with more complex problems.
-
Standardization: Presenting answers in their simplest form is a standard practice in mathematics to ensure consistency and clarity.
Illustrative Examples: Extending the Concept
Let's extend our understanding by looking at other fractions and applying the simplification techniques:
-
24/36: The GCD of 24 and 36 is 12. Therefore, 24/36 simplifies to 2/3.
-
42/63: The GCD of 42 and 63 is 21. Therefore, 42/63 simplifies to 2/3.
-
105/135: Using prime factorization: 105 = 3 x 5 x 7 and 135 = 3³ x 5. The GCD is 3 x 5 = 15. Therefore, 105/135 simplifies to 7/9.
These examples demonstrate that different fractions can simplify to the same reduced form. This illustrates the concept of equivalent fractions – fractions that represent the same value, even if they look different.
Further Exploration: Improper Fractions and Mixed Numbers
So far, we've focused on proper fractions (where the numerator is smaller than the denominator). Let's briefly consider improper fractions (where the numerator is larger than or equal to the denominator) and mixed numbers.
An improper fraction can be simplified just like a proper fraction. For example, 21/6 simplifies to 7/2 (GCD is 3). An improper fraction can also be expressed as a mixed number – a whole number and a proper fraction. 7/2 can be written as 3½. The simplification process remains the same regardless of whether you are working with an improper fraction or a mixed number; you still aim to reduce the fractional part to its lowest terms.
Frequently Asked Questions (FAQ)
Q: What if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. It cannot be simplified further.
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
A: No, you must divide both the numerator and the denominator by the same number to maintain the value of the fraction. Dividing by different numbers will change the fractional value.
Q: Is there a quick way to tell if a fraction is simplified?
A: Check if the numerator and denominator share any common factors other than 1. If they don't, the fraction is simplified.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill that underpins many mathematical concepts. By mastering the techniques outlined – using the GCD, prime factorization, or stepwise simplification – you’ll improve your mathematical accuracy, efficiency, and understanding. Remember, the goal is always to express the fraction in its simplest form, where the numerator and denominator share no common factors other than 1. With practice, simplifying fractions will become second nature, empowering you to tackle more complex mathematical challenges with confidence. The example of 18/30, simplified to 3/5, serves as a perfect starting point for developing this crucial skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Simplify 18 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.