Simplify 14 30
stanleys
Sep 21, 2025 · 6 min read
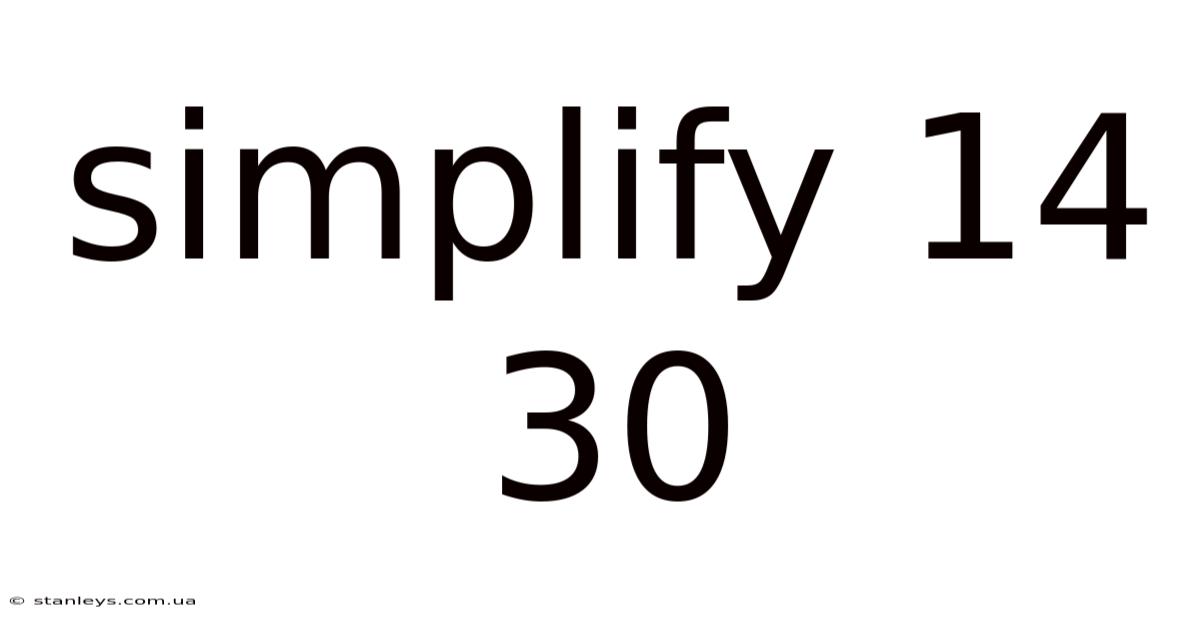
Table of Contents
Simplifying Fractions: A Deep Dive into 14/30
Understanding how to simplify fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This comprehensive guide will walk you through the process of simplifying the fraction 14/30, explaining the underlying concepts and offering practical examples to solidify your understanding. We'll explore the concept of greatest common divisors (GCD), prime factorization, and offer tips and tricks to make simplifying fractions a breeze. This detailed explanation will equip you with the knowledge to tackle any fraction simplification problem with confidence.
Introduction: What Does Simplifying Fractions Mean?
Simplifying a fraction means reducing it to its simplest form. This means finding an equivalent fraction where the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. In simpler terms, you're finding the smallest possible whole numbers that represent the same ratio. For example, the fraction 2/4 can be simplified to 1/2 because both 2 and 4 are divisible by 2. We'll apply this same principle to simplify 14/30.
Step-by-Step Simplification of 14/30
To simplify 14/30, we need to find the greatest common divisor (GCD) of 14 and 30. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. There are a few ways to find the GCD:
1. Listing Factors:
- Factors of 14: 1, 2, 7, 14
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
By comparing the lists, we see that the largest common factor is 2.
2. Prime Factorization:
This method is particularly useful for larger numbers. We break down each number into its prime factors (numbers divisible only by 1 and themselves):
- Prime factorization of 14: 2 x 7
- Prime factorization of 30: 2 x 3 x 5
The common prime factor is 2. Therefore, the GCD is 2.
3. Euclidean Algorithm:
This is a more systematic approach, especially helpful for larger numbers. It involves repeatedly dividing the larger number by the smaller number and taking the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 30 by 14: 30 = 14 x 2 + 2
- Divide 14 by 2: 14 = 2 x 7 + 0
The last non-zero remainder is 2, so the GCD is 2.
Now that we've found the GCD (2), we can simplify the fraction:
14 ÷ 2 / 30 ÷ 2 = 7/15
Therefore, the simplified form of 14/30 is 7/15.
A Deeper Look: Understanding Greatest Common Divisors (GCD)
The GCD is the cornerstone of fraction simplification. Finding the GCD efficiently is key to simplifying fractions quickly and accurately. As demonstrated above, there are several methods to find the GCD. Choosing the most efficient method depends on the complexity of the numbers involved. For smaller numbers, listing factors might be sufficient. For larger numbers, prime factorization or the Euclidean algorithm are more efficient.
The Euclidean algorithm, although slightly more complex initially, offers a systematic approach that works flawlessly for any pair of numbers. It's particularly useful when dealing with larger numbers where listing factors would be tedious and error-prone.
Prime Factorization: A Powerful Tool
Prime factorization is a powerful technique not just for simplifying fractions but also for various other mathematical operations. Understanding how to decompose numbers into their prime factors can significantly improve your problem-solving skills. It provides a structured way to find common factors, which are essential for simplifying fractions and performing other calculations like finding the least common multiple (LCM).
Visualizing Fraction Simplification
Imagine a pizza cut into 30 slices. The fraction 14/30 represents having 14 out of 30 slices. To simplify this, we can group the slices. Since we found the GCD to be 2, we can group the slices into pairs. We'll have 7 pairs of slices out of 15 total pairs. This visually represents the simplified fraction 7/15. This visual approach can be helpful, especially for beginners, to grasp the concept of fraction equivalence.
Beyond 14/30: Applying the Techniques
The techniques we used to simplify 14/30 are applicable to any fraction. Let's consider a few examples:
- Simplify 18/24: The GCD of 18 and 24 is 6. 18 ÷ 6 / 24 ÷ 6 = 3/4
- Simplify 25/75: The GCD of 25 and 75 is 25. 25 ÷ 25 / 75 ÷ 25 = 1/3
- Simplify 36/48: The GCD of 36 and 48 is 12. 36 ÷ 12 / 48 ÷ 12 = 3/4
These examples demonstrate the versatility of the GCD and prime factorization in simplifying fractions of varying complexities. Practice is key to mastering these techniques.
Frequently Asked Questions (FAQ)
Q: What if I don't find the greatest common divisor?
A: If you don't find the greatest common divisor initially, you can still simplify the fraction by dividing the numerator and the denominator by any common factor. You might need to repeat the process until you reach the simplest form. However, using the GCD ensures you reach the simplest form in a single step.
Q: Can I simplify fractions with decimals?
A: No, the process of simplifying fractions applies only to fractions with whole numbers in the numerator and denominator. If you have decimals, you first need to convert them to fractions before simplifying.
Q: Is there a shortcut to simplify fractions?
A: While there isn't a magical shortcut to always bypass finding the GCD, practicing the different methods will help you develop an intuition for common factors, speeding up the process over time. Familiarity with common multiples and prime numbers is also extremely helpful.
Q: Why is simplifying fractions important?
A: Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret than complex ones.
- Accuracy: Simplified fractions are more accurate in calculations, especially when dealing with multiple fractions.
- Efficiency: Simplified fractions make calculations much more efficient and less prone to errors.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill that underpins many mathematical concepts. By understanding the concept of the greatest common divisor, employing methods like prime factorization or the Euclidean algorithm, and practicing regularly, you can confidently tackle any fraction simplification problem. Remember, the key is to find the greatest common divisor of the numerator and denominator and then divide both by that number. This guide provides a thorough understanding of simplifying fractions, empowering you to solve problems with accuracy and efficiency. Practice makes perfect, so keep working with different examples to solidify your understanding and build your mathematical skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Simplify 14 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.