Factorise 5x 10
stanleys
Sep 17, 2025 · 5 min read
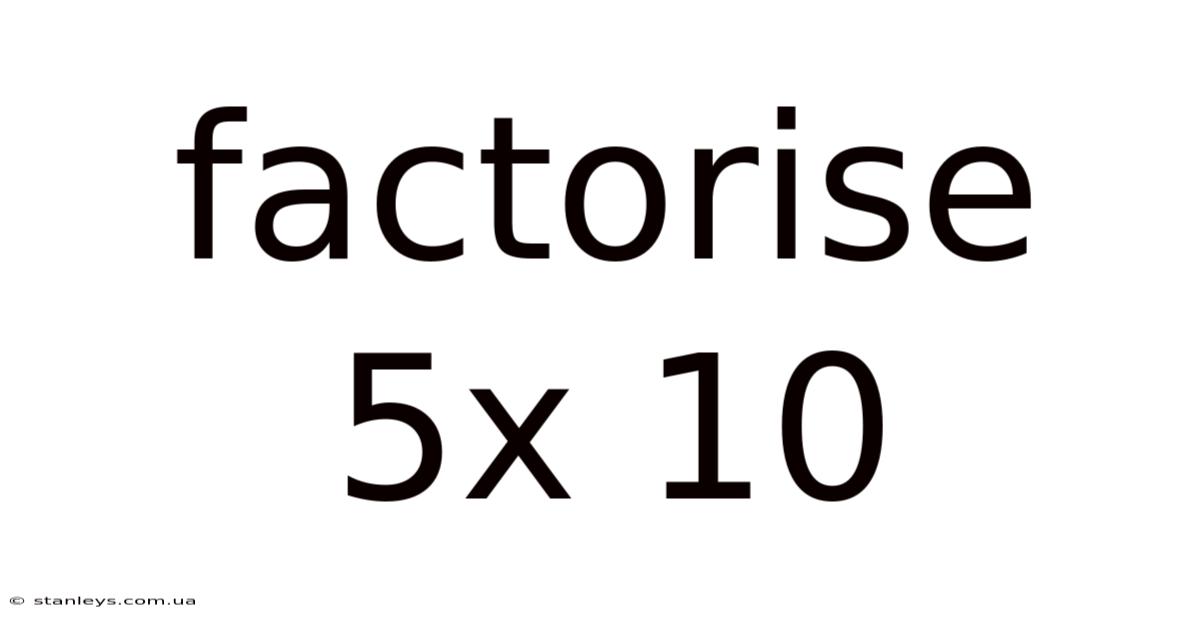
Table of Contents
Factorising 5x + 10: A Comprehensive Guide
This article will delve into the seemingly simple task of factorising the algebraic expression 5x + 10. While the process might appear straightforward at first glance, understanding the underlying principles and exploring various approaches will solidify your grasp of fundamental algebraic concepts. We'll move beyond a simple solution to explore the broader implications and applications of factorisation. This understanding is crucial for more advanced algebraic manipulations and problem-solving in areas like calculus, equation solving, and graphing.
Introduction to Factorisation
Factorisation, in its essence, is the process of breaking down a mathematical expression into smaller, simpler components – its factors – that when multiplied together, give you the original expression. Think of it like reverse multiplication. For example, factoring 12 might yield 2 x 2 x 3, or 4 x 3, etc. These are all the factors of 12. In algebra, we apply the same principle to algebraic expressions. Factorisation is a powerful tool used to simplify complex equations, solve for unknowns, and gain a deeper understanding of the underlying mathematical relationships.
Step-by-Step Factorisation of 5x + 10
The expression 5x + 10 is a binomial (meaning it contains two terms). To factorise it, we look for the greatest common factor (GCF) of the two terms, 5x and 10.
-
Identify the coefficients: The coefficients are the numerical parts of the terms. In 5x, the coefficient is 5, and in 10, the coefficient is 10.
-
Find the greatest common factor (GCF) of the coefficients: The GCF of 5 and 10 is 5. This is because 5 is the largest number that divides evenly into both 5 and 10.
-
Identify the common variables (if any): Both terms do not share a common variable. The first term has an 'x', but the second term does not. Therefore, there is no common variable factor.
-
Factor out the GCF: We take the GCF, which is 5, and place it outside parentheses. Inside the parentheses, we write what remains when we divide each term by the GCF.
5x / 5 = x 10 / 5 = 2
Therefore, the factorised form of 5x + 10 is: 5(x + 2)
This means that 5 multiplied by (x + 2) equals 5x + 10. You can easily verify this by expanding the factored expression: 5(x + 2) = 5x + 10.
Understanding the Concept of Factors
The factors of 5x + 10 are 5 and (x + 2). These are the building blocks that, when multiplied, reconstruct the original expression. Understanding factors is crucial for solving equations and simplifying expressions. For example, if we have the equation 5x + 10 = 0, we can use the factored form to easily solve for x:
5(x + 2) = 0
This equation is true if either 5 = 0 (which is false) or (x + 2) = 0. Solving for x in the second case gives us x = -2.
This simple example highlights the power of factorisation in solving equations. Without factorisation, solving 5x + 10 = 0 would require more complex algebraic manipulations.
Expanding on Factorisation Techniques
While the factorisation of 5x + 10 involved a simple GCF, more complex expressions require different techniques. Here are some examples:
-
Difference of Squares: Expressions in the form a² - b² can be factorised as (a + b)(a - b). For example, x² - 9 factorises to (x + 3)(x - 3).
-
Quadratic Trinomials: Expressions in the form ax² + bx + c can often be factorised into two binomial expressions. This usually involves finding two numbers that add up to 'b' and multiply to 'ac'.
-
Grouping: For expressions with four or more terms, grouping similar terms together can help reveal common factors.
These are just a few of the various techniques used in factorisation. The choice of method depends on the structure and complexity of the algebraic expression.
The Importance of Factorisation in Advanced Mathematics
The seemingly simple process of factorisation forms the foundation for numerous advanced mathematical concepts:
-
Solving Polynomial Equations: Factorisation is essential for solving higher-degree polynomial equations. By factoring the polynomial, you can find its roots (the values of x that make the polynomial equal to zero).
-
Calculus: Factorisation simplifies expressions, making differentiation and integration significantly easier. In calculus, simplifying expressions is crucial for finding derivatives, integrals, and understanding the behaviour of functions.
-
Graphing: The factored form of a polynomial expression reveals important information about its graph, such as its x-intercepts (where the graph crosses the x-axis).
-
Linear Algebra: Factorisation plays a role in matrix operations and solving systems of linear equations.
Real-World Applications of Factorisation
While seemingly abstract, factorisation finds applications in various real-world scenarios:
-
Engineering: Engineers use factorisation to simplify complex equations and models in structural design, fluid dynamics, and electrical circuits.
-
Physics: Factorisation simplifies equations describing motion, forces, and energy.
-
Economics: Factorisation can be used to model and analyze economic relationships and predict trends.
-
Computer Science: Factorisation is used in cryptography and algorithm design.
Frequently Asked Questions (FAQ)
-
Q: What if the expression doesn't have a common factor?
A: If the terms in an expression share no common factors (other than 1), then the expression is considered to be already in its simplest factored form. It's prime.
-
Q: Can I factorise 5x + 10 in different ways?
A: While 5(x + 2) is the most simplified form, you could technically write it as (5/2)(2x + 4) but that is less simplified and generally not preferred.
-
Q: What happens if I have a negative GCF?
A: You can factor out a negative GCF. For example, if you have -5x -10, you could factor out -5, resulting in -5(x + 2). This is perfectly acceptable.
Conclusion: Mastering Factorisation
Factorising the expression 5x + 10, while simple in its execution, serves as a gateway to understanding more complex algebraic manipulations. The ability to factorise efficiently and accurately is a foundational skill in algebra and is crucial for success in more advanced mathematical studies and various real-world applications. By mastering this fundamental technique, you equip yourself with a powerful tool for problem-solving and a deeper appreciation of the underlying structure of mathematical expressions. Remember that consistent practice and a thorough understanding of the different factorisation techniques are key to developing fluency and confidence in this crucial algebraic skill. Don't hesitate to explore different expressions and challenge yourself with increasingly complex examples to solidify your understanding.
Latest Posts
Latest Posts
-
Merry Cone Spanish
Sep 17, 2025
-
9 Times 4
Sep 17, 2025
-
235 Kph Mph
Sep 17, 2025
-
Calcium Hydrochloric Acid
Sep 17, 2025
-
21km In Miles
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Factorise 5x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.