Factorise 2x 10
stanleys
Sep 14, 2025 · 5 min read
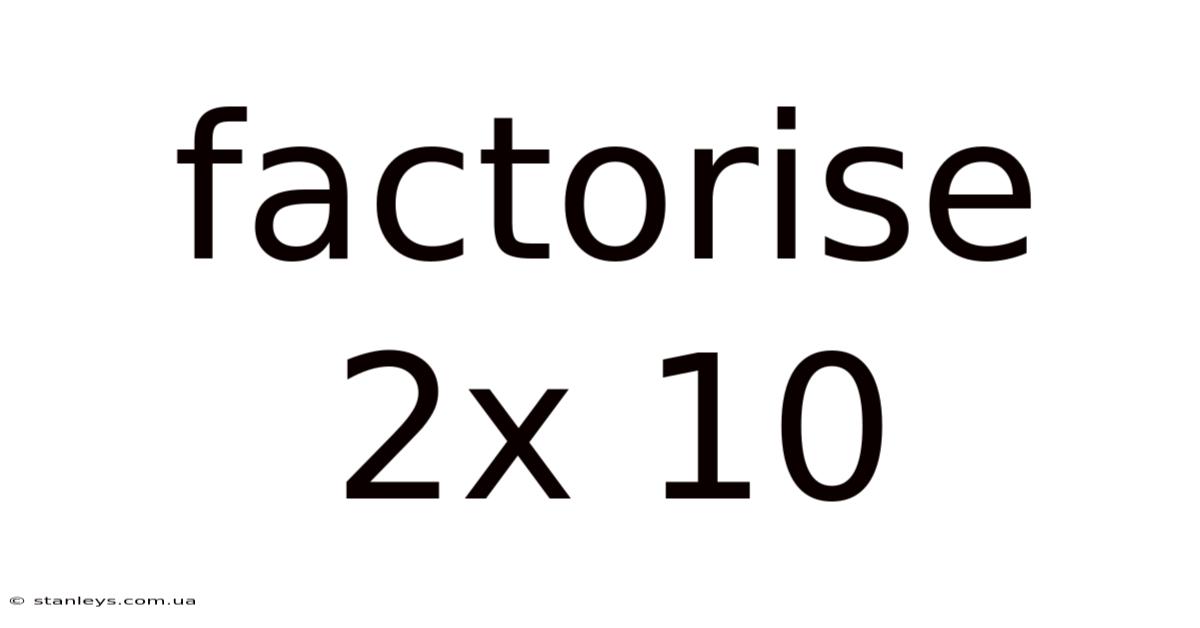
Table of Contents
Factorising 2x + 10: A Comprehensive Guide
Introduction:
This article provides a comprehensive guide to factorising the algebraic expression 2x + 10. We will explore different methods for factorisation, delve into the underlying mathematical principles, and address common questions students might have. Understanding factorisation is crucial for further algebraic manipulations, solving equations, and simplifying complex expressions. This seemingly simple problem opens a door to a deeper understanding of fundamental algebraic concepts. We'll cover everything from the basics of the greatest common factor (GCF) to more advanced techniques. By the end, you'll not only be able to factorise 2x + 10 but also understand the broader implications of this process in algebra.
Understanding Factorisation
Before we tackle 2x + 10, let's clarify what factorisation actually means. Factorisation, also known as factoring, is the process of breaking down a mathematical expression into smaller, simpler expressions that, when multiplied together, give the original expression. Think of it like reverse multiplication. For example, the number 12 can be factorised as 2 x 6, 3 x 4, or 2 x 2 x 3. Similarly, algebraic expressions can be factorised into simpler terms.
Finding the Greatest Common Factor (GCF)
The most straightforward method for factorising many algebraic expressions, including 2x + 10, involves identifying the greatest common factor (GCF) of the terms. The GCF is the largest number or term that divides evenly into all terms of the expression.
Let's look at our expression, 2x + 10:
- 2x: The terms are 2 and x.
- 10: The factors are 2 and 5.
Both 2x and 10 share a common factor of 2. Therefore, the GCF of 2x and 10 is 2.
Factorising 2x + 10 using the GCF
Now that we've identified the GCF as 2, we can factor it out of the expression:
2x + 10 = 2(x + 5)
To verify this, we can expand the factored expression using the distributive property:
2(x + 5) = 2 * x + 2 * 5 = 2x + 10
This confirms that our factorisation is correct. The expression 2x + 10 is now factored into 2 and (x + 5).
Visualising Factorisation
Imagine you have 2x apples and 10 oranges. You can group these fruits into two equal groups. Each group would contain x apples and 5 oranges. This visual representation helps demonstrate the concept of factoring out the common factor (2 in this case) to simplify the expression.
Applications of Factorisation
Factorisation is a fundamental skill in algebra with numerous applications:
-
Solving Quadratic Equations: Factorisation is a key technique used to solve quadratic equations (equations of the form ax² + bx + c = 0). By factoring the quadratic expression, you can find the values of x that satisfy the equation.
-
Simplifying Expressions: Factorisation simplifies complex algebraic expressions, making them easier to understand and manipulate. This is particularly useful when dealing with fractions involving algebraic expressions.
-
Finding Roots and Zeros: In function analysis, factorisation helps in finding the roots (or zeros) of a function, which are the points where the function intersects the x-axis.
-
Calculus: Factorisation is essential in calculus for simplifying expressions and solving problems related to derivatives and integrals.
Further Exploration of Factorisation Techniques
While the GCF method is sufficient for 2x + 10, more complex algebraic expressions require other factorisation techniques:
-
Difference of Squares: This technique applies to expressions of the form a² - b², which factorises to (a + b)(a - b).
-
Trinomial Factoring: This involves factorising quadratic trinomials (expressions of the form ax² + bx + c) into two binomial factors. Various methods exist for trinomial factoring, such as the AC method and grouping.
-
Grouping: This method is used when an expression contains four or more terms. It involves grouping terms with common factors and then factoring out the common factors from each group.
Frequently Asked Questions (FAQ)
Q1: Is there only one way to factorise 2x + 10?
A1: No, while 2(x + 5) is the most simplified form, technically you could also factor it as other equivalent forms, like (-2)(-x-5). However, 2(x + 5) is considered the standard and most useful form.
Q2: What if the expression doesn't have a common factor?
A2: If the terms of an expression share no common factors other than 1, then the expression is considered to be already in its simplest factored form.
Q3: How can I improve my factorisation skills?
A3: Practice is key! Work through various examples of different complexity. Start with simple expressions and gradually move towards more challenging ones. Using online resources and textbooks with practice problems can greatly improve your skills.
Q4: What happens if I make a mistake during factorisation?
A4: You can always check your answer by expanding the factored expression using the distributive property. If you get the original expression, your factorisation is correct. If not, re-examine your steps to identify the error.
Advanced Concepts Related to Factorisation
-
Prime Factorisation: This involves expressing a number or polynomial as a product of its prime factors (factors that are only divisible by 1 and themselves). Prime factorisation is fundamental in number theory and algebra.
-
Polynomial Factorisation: This involves factorising polynomials of higher degrees (e.g., cubic, quartic polynomials). Various techniques exist for factorising these more complex polynomials.
Conclusion
Factorising the expression 2x + 10, while seemingly simple, provides a solid foundation for understanding more complex algebraic manipulations. By identifying the greatest common factor (GCF) of 2, we efficiently factorise the expression as 2(x + 5). This simple example highlights the importance of GCF in simplifying expressions and opens the door to understanding more advanced techniques in algebra and their applications in various mathematical fields. Mastering factorisation skills will significantly enhance your ability to solve equations, simplify expressions, and tackle more complex mathematical problems in the future. Remember, consistent practice is the key to developing proficiency in factorisation.
Latest Posts
Latest Posts
-
178kg In Stone
Sep 14, 2025
-
96 5kg To Stone
Sep 14, 2025
-
109kg In Lbs
Sep 14, 2025
-
73inches In Feet
Sep 14, 2025
-
Uniform Layer Haircut
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factorise 2x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.