9 20 Decimal
stanleys
Sep 14, 2025 · 6 min read
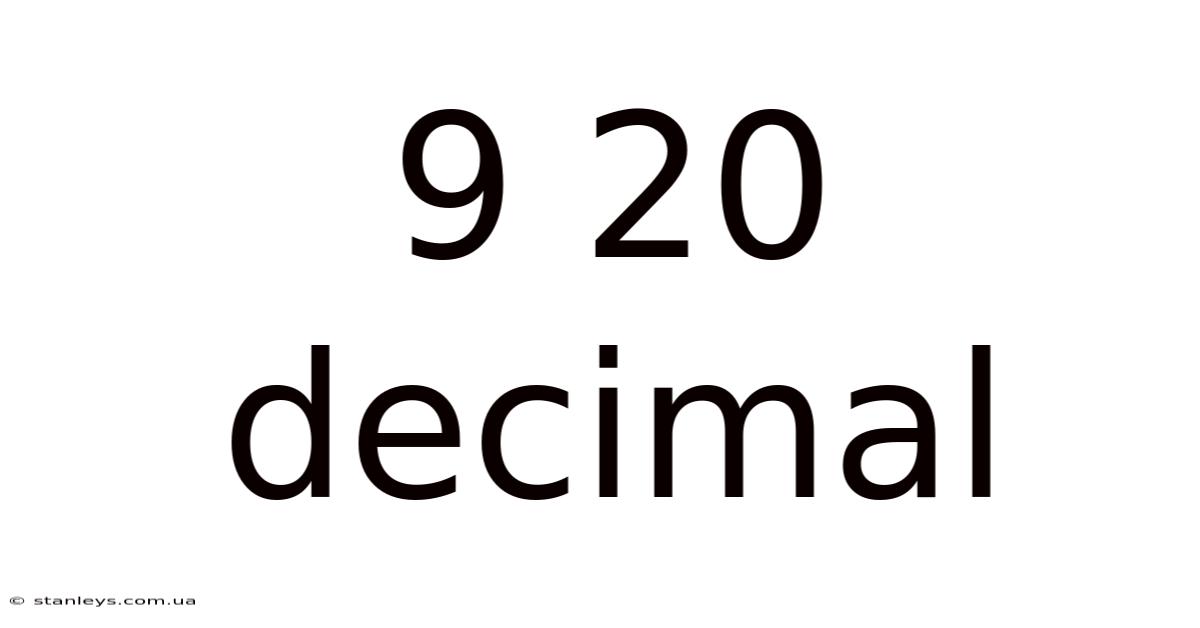
Table of Contents
Decoding 9.20 Decimal: A Deep Dive into its Mathematical and Practical Significance
Understanding decimal numbers is fundamental to mathematics and numerous applications in daily life. This article delves deep into the seemingly simple decimal number 9.20, exploring its mathematical representation, different interpretations, practical applications, and addressing frequently asked questions. We'll move beyond a superficial understanding to reveal the rich tapestry of concepts woven into this seemingly straightforward number.
Introduction: What is 9.20?
The decimal number 9.20 represents a value between 9 and 10. It signifies nine whole units and two tenths of a unit. The digit to the left of the decimal point (9) indicates the whole number part, while the digits to the right (20) represent the fractional part. Understanding the positional value of each digit is crucial: the 2 represents two tenths (2/10 or 0.2), and the 0 in the hundredths place signifies zero hundredths (0/100 or 0.00). While 9.2 and 9.20 are numerically equivalent, the inclusion of the trailing zero can be significant depending on the context, often indicating a higher level of precision or measurement accuracy.
Understanding Decimal Representation
Decimal numbers are based on a base-10 system, meaning each place value represents a power of 10. Moving from right to left, the place values are: tenths (10⁻¹), hundredths (10⁻²), thousandths (10⁻³), and so on. Similarly, moving from the decimal point to the left, the place values are ones (10⁰), tens (10¹), hundreds (10²), thousands (10³), and so forth. Thus, 9.20 can be expressed as:
9 × 10⁰ + 2 × 10⁻¹ + 0 × 10⁻² = 9 + 0.2 + 0 = 9.2
This breakdown clarifies the contribution of each digit to the overall value. The zero in the hundredths place, though seemingly insignificant, highlights the precision of the measurement. It indicates that the value is precisely 9.20 and not, for example, a rounded value like 9.21 or 9.19.
Different Interpretations and Contexts
The interpretation of 9.20 depends heavily on the context. Here are some examples:
-
Measurement: In scientific measurements, 9.20 could represent a length (9.20 meters), weight (9.20 grams), or volume (9.20 liters). The inclusion of the zero emphasizes the measurement precision to the nearest hundredth. A scientist might use 9.20 cm to denote a measurement accurate to the nearest 0.01 centimeters, a level of precision not implied by 9.2 cm.
-
Money: In financial contexts, 9.20 could represent a monetary value (e.g., $9.20, €9.20). The zero signifies the absence of cents or smaller subdivisions of the currency.
-
Grading: In some grading systems, 9.20 might represent a score or rating on a scale. The precision indicates a more refined assessment than a simpler 9.2.
-
Data Representation: In computer science, 9.20 might be a floating-point number. While computers often handle decimal numbers using binary representation, the concept of decimal precision remains relevant.
-
Statistical Analysis: In statistical analysis, 9.20 could be a calculated average, a measurement of deviation, or other numerical data. The significance of the '0' depends on the precision of the data collection method and the scale of the measurements.
Practical Applications of Decimal Numbers Like 9.20
Decimal numbers are ubiquitous in everyday life. Here are some examples of where 9.20, or numbers like it, are practically used:
- Shopping: Calculating prices, discounts, and tax.
- Cooking: Measuring ingredients accurately for recipes.
- Engineering: Designing and building structures, machines, and tools.
- Science: Conducting experiments, analyzing data, and reporting results.
- Finance: Managing budgets, investments, and financial transactions.
- Sports: Tracking scores, statistics, and performance metrics.
- Geography: Measuring distances, areas, and elevations.
These applications highlight the widespread use of decimal numbers in our interactions with the world. The precision offered by the extra digit (the 0 in 9.20) improves accuracy and efficiency across all these contexts.
Representing 9.20 in Different Number Systems
While we primarily use the decimal system (base-10), it's instructive to explore how 9.20 is represented in other number systems. Let's look at the binary (base-2) system, commonly used in computers:
Converting 9.20 to binary requires converting the integer and fractional parts separately. 9 in decimal is 1001 in binary. Converting the fractional part (0.2) is more complex. Repeatedly multiplying by 2 and taking the integer part will give an approximate binary representation: 0.00110011... This is a repeating binary fraction, demonstrating that some decimal numbers do not have exact binary equivalents. This is a key concept in understanding potential rounding errors in computer calculations involving decimal numbers.
Common Mistakes and Misconceptions
-
Ignoring trailing zeros: Sometimes, students might mistakenly believe that 9.2 and 9.20 are not equivalent. While numerically they are the same, the trailing zero often signifies increased precision or accuracy of measurement.
-
Confusing decimal places with significant figures: The number of decimal places (in this case, two) is not always equivalent to the number of significant figures. Significant figures refer to the number of meaningful digits in a value. In this case, 9.20 has three significant figures.
-
Incorrect rounding: Rounding 9.20 to one decimal place would correctly result in 9.2, but rounding inaccurately (e.g., to 9.0) introduces error.
Frequently Asked Questions (FAQs)
-
Q: What is the difference between 9.2 and 9.20?
- A: Numerically, there is no difference. However, 9.20 suggests a higher degree of precision or accuracy in measurement or calculation than 9.2.
-
Q: How do I convert 9.20 to a fraction?
- A: 9.20 can be expressed as 9 and 20/100, which simplifies to 9 and 2/10, or 9 and 1/5. This equals 46/5.
-
Q: How can I convert 9.20 to a percentage?
- A: To express 9.20 as a percentage, multiply by 100: 9.20 x 100 = 920%.
-
Q: Can 9.20 be expressed as a mixed number?
- A: Yes, as shown above, it can be expressed as 9 1/5.
-
Q: What are the significant figures in 9.20?
- A: There are three significant figures in 9.20. All digits are considered significant because they contribute to the precision of the measurement.
Conclusion: The Significance of Precision
This in-depth exploration of the decimal number 9.20 demonstrates that even seemingly simple numbers can hold significant mathematical and practical implications. The inclusion of the trailing zero in 9.20 highlights the importance of precision in various fields, from scientific measurements to financial calculations. Understanding the different interpretations and applications of decimal numbers, including their representation in other number systems, is crucial for effective problem-solving and a comprehensive understanding of mathematics. By appreciating the nuances of decimal notation, we can better interpret data, solve problems, and enhance our understanding of the numerical world around us. The seemingly simple 9.20 serves as a microcosm of the power and precision embedded within the decimal system, a cornerstone of our mathematical and scientific endeavors.
Latest Posts
Latest Posts
-
70 Mph Kmh
Sep 14, 2025
-
Burgundy Coat Dog
Sep 14, 2025
-
17cms In Inches
Sep 14, 2025
-
35pounds To Kg
Sep 14, 2025
-
70 Of 65
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 9 20 Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.