85 Of 480
stanleys
Sep 16, 2025 · 5 min read
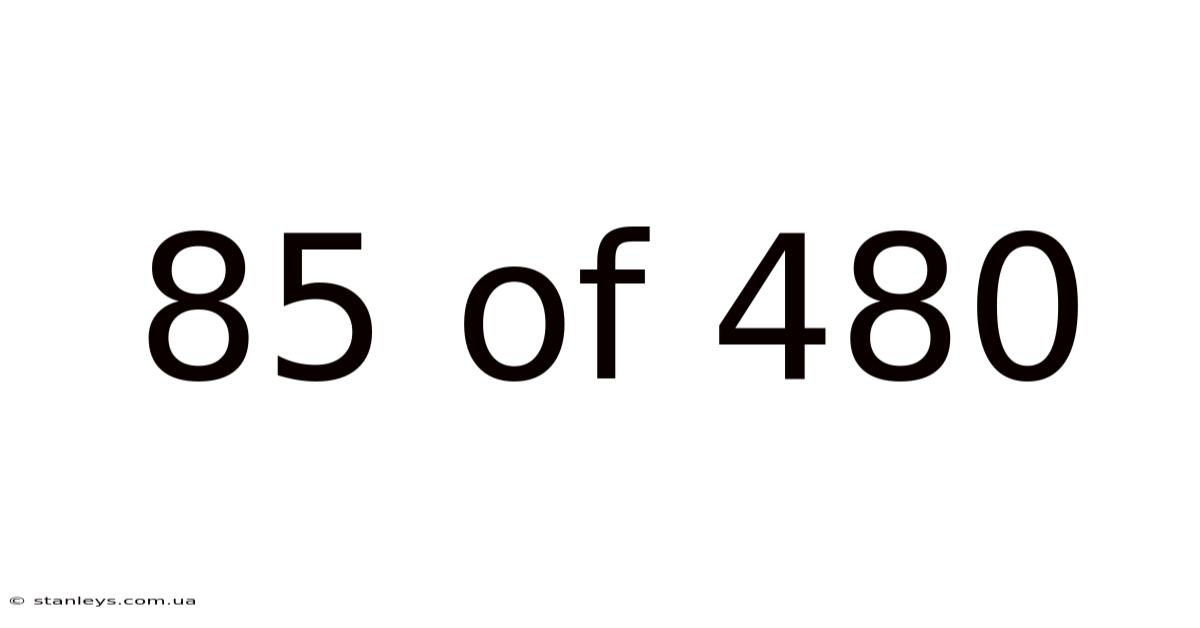
Table of Contents
Decoding the Fraction: Understanding and Solving 85/480
This article will delve into the intricacies of the fraction 85/480, exploring various methods of simplification, its decimal equivalent, and its application in real-world scenarios. Understanding fractions is fundamental to mathematics, and mastering the simplification and manipulation of fractions like 85/480 builds a strong foundation for more advanced mathematical concepts. We'll cover the core principles, provide step-by-step solutions, and address frequently asked questions, aiming to make this seemingly complex topic easily accessible.
Introduction: Why 85/480 Matters
The fraction 85/480, while seemingly simple at first glance, represents a crucial concept in arithmetic and lays the groundwork for algebra, calculus, and other higher-level mathematical disciplines. The ability to simplify fractions, understand their decimal equivalents, and apply them to practical problems is a valuable skill applicable across numerous fields, from engineering and finance to cooking and construction. This article serves as a comprehensive guide to mastering this specific fraction, while simultaneously providing a broader understanding of fraction manipulation.
Step-by-Step Simplification of 85/480
Simplifying a fraction involves reducing it to its lowest terms – finding the greatest common divisor (GCD) of the numerator (85) and the denominator (480) and dividing both by it. Let's break down the process:
-
Finding the GCD: To find the greatest common divisor of 85 and 480, we can use the Euclidean algorithm or prime factorization. Let's opt for prime factorization:
- Prime factorization of 85: 5 x 17
- Prime factorization of 480: 2 x 2 x 2 x 2 x 2 x 3 x 5
-
Identifying Common Factors: Comparing the prime factorizations, we see that the only common factor is 5.
-
Simplifying the Fraction: Dividing both the numerator and the denominator by the GCD (5):
- 85 ÷ 5 = 17
- 480 ÷ 5 = 96
Therefore, the simplified form of 85/480 is 17/96. This simplified fraction is now in its lowest terms, meaning there are no more common factors between the numerator and the denominator other than 1.
Converting 17/96 to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
17 ÷ 96 ≈ 0.17708333...
The result is a recurring decimal, meaning the digits after the decimal point repeat infinitely. For practical purposes, we can round the decimal to a certain number of decimal places, depending on the required level of accuracy. For example, rounded to three decimal places, 17/96 ≈ 0.177.
Illustrative Examples: Real-World Applications
Understanding fractions like 17/96 allows us to solve various real-world problems. Let's consider a few scenarios:
-
Baking: If a recipe calls for 480 grams of flour and you only want to make a smaller portion equivalent to 85 grams of flour, you'd be using 85/480 or 17/96 of the recipe. This simplified fraction makes it easier to adjust the quantities of other ingredients proportionally.
-
Engineering: In engineering design, fractions are frequently used to represent ratios and proportions. For example, 17/96 could represent a scale factor in a blueprint or the ratio of components in a mixture.
-
Finance: Fractions are used extensively in finance to represent percentages, proportions of investments, or parts of a whole. Understanding fraction manipulation is critical for accurate financial calculations.
-
Probability: In probability, fractions represent the likelihood of an event occurring. For instance, if there are 96 equally likely outcomes and 17 are favorable, the probability of the favorable outcome would be 17/96.
Percentage Equivalent of 85/480 (or 17/96)
To express the fraction 17/96 as a percentage, we multiply the decimal equivalent by 100:
0.17708333... x 100 ≈ 17.71%
Therefore, 85/480 is approximately 17.71%.
Further Mathematical Explorations
The simplification of 85/480 and its conversion to a decimal and percentage provide a foundation for more complex mathematical operations. We can explore operations such as:
-
Addition and Subtraction of Fractions: Adding or subtracting fractions requires a common denominator. While 17/96 is already simplified, if we were dealing with other fractions, we would need to find the least common multiple (LCM) to obtain a common denominator before performing the operation.
-
Multiplication and Division of Fractions: Multiplying fractions involves multiplying the numerators and the denominators separately. Dividing fractions involves inverting the second fraction and then multiplying.
-
Working with Mixed Numbers: If we were dealing with mixed numbers (a whole number and a fraction), we would convert them to improper fractions before performing any operations.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 85/480?
A1: The simplest form of 85/480 is 17/96.
Q2: How do I convert 85/480 to a decimal?
A2: Divide the numerator (85) by the denominator (480). This yields approximately 0.177.
Q3: What is the percentage equivalent of 85/480?
A3: The percentage equivalent of 85/480 is approximately 17.71%.
Q4: What if the GCD wasn't easily identifiable through prime factorization?
A4: If the prime factorization method is cumbersome, the Euclidean algorithm provides an alternative and efficient method for finding the GCD of two numbers.
Q5: Are there any online calculators to verify the simplification?
A5: Yes, numerous online fraction calculators are available to verify the simplification process and decimal/percentage conversions. However, understanding the underlying principles is crucial for building mathematical proficiency.
Conclusion: Mastering Fractions – A Building Block for Success
Mastering the simplification and manipulation of fractions like 85/480 is a critical step in developing a strong mathematical foundation. This article provided a detailed explanation of the simplification process, conversion to decimals and percentages, and real-world applications. The ability to confidently work with fractions is not only essential for academic success but also empowers you to tackle various real-world challenges requiring proportional reasoning and numerical analysis. Remember, consistent practice and a clear understanding of the fundamental principles are key to building confidence and mastery in this crucial area of mathematics. Continue exploring further mathematical concepts, building upon this strong foundation you’ve developed.
Latest Posts
Related Post
Thank you for visiting our website which covers about 85 Of 480 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.