75 X 5
stanleys
Sep 11, 2025 · 6 min read
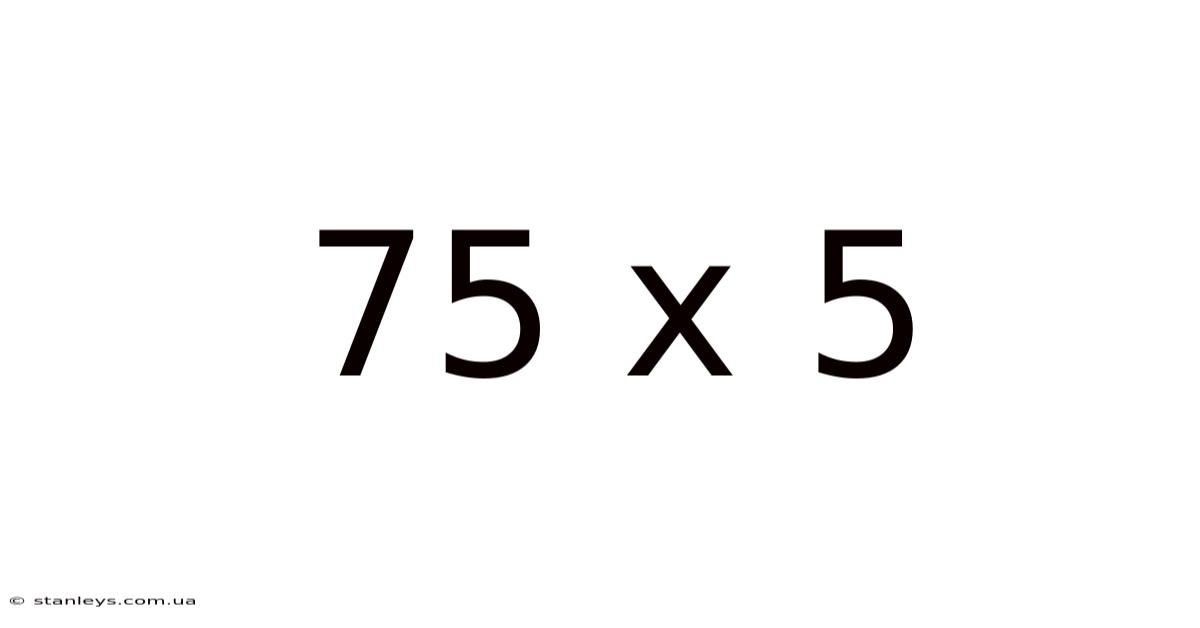
Table of Contents
Unlocking the Power of 75 x 5: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem 75 x 5, delving far beyond the basic answer. We'll uncover various methods for solving it, examine its applications in real-world scenarios, and explore the underlying mathematical concepts. Understanding this seemingly simple calculation opens doors to a deeper appreciation of mathematics and its practical utility. This exploration will be beneficial for students, teachers, and anyone curious about the fascinating world of numbers.
I. Introduction: More Than Just an Answer
At first glance, 75 x 5 appears straightforward. A quick calculation reveals the answer: 375. However, this seemingly simple equation serves as a gateway to understanding fundamental mathematical principles and their practical applications across various fields. This article aims to dissect this problem, revealing the different approaches to solving it and highlighting its significance in everyday life and beyond. We will delve into the methods, explore real-world applications, and consider the broader mathematical context.
II. Methods for Solving 75 x 5
Several methods can be employed to solve 75 x 5, each offering unique insights into the multiplication process. Let's explore some of these:
-
Standard Multiplication: This is the most common method taught in schools. It involves multiplying each digit of 75 by 5, starting with the ones place and carrying over any tens digit.
75 x 5 --- 375 -
Distributive Property: This method utilizes the distributive property of multiplication over addition, breaking down the problem into smaller, more manageable parts. We can rewrite 75 as 70 + 5, then distribute the 5:
5 x (70 + 5) = (5 x 70) + (5 x 5) = 350 + 25 = 375
-
Mental Math Techniques: For those comfortable with mental arithmetic, several shortcuts exist. One approach is to multiply 75 by 10 (which is easily done by adding a zero), then halving the result:
75 x 10 = 750 750 / 2 = 375
-
Repeated Addition: While less efficient for larger numbers, this method involves adding 75 five times:
75 + 75 + 75 + 75 + 75 = 375
-
Using a Calculator: In situations where speed and accuracy are paramount, a calculator provides a rapid solution. However, understanding the underlying principles remains crucial, even when using technology.
III. Real-World Applications of 75 x 5
The multiplication of 75 by 5, while seemingly abstract, has numerous practical applications in everyday life:
-
Shopping: Imagine buying five items costing $75 each. The total cost is easily calculated as 75 x 5 = $375.
-
Measurement: If you need five pieces of wood, each 75 centimeters long, the total length needed is 375 centimeters.
-
Cooking and Baking: Many recipes involve multiplying ingredients. For example, if a recipe calls for 75 grams of flour and you need to make five times the recipe, you'll need 375 grams of flour.
-
Finance: Calculating interest, discounts, or profit margins often involves multiplication. For instance, if you earn a 5% commission on $75, your commission would be $3.75 (75 x 0.05 = 3.75).
-
Construction and Engineering: Calculations involving area, volume, and material quantities frequently utilize multiplication. For example, calculating the area of five squares, each with sides of 75 units, involves 75 x 75 x 5 = 28125 square units.
These are just a few examples. The application of 75 x 5, and multiplication in general, extends to countless scenarios in various professions and aspects of daily life.
IV. Exploring the Mathematical Concepts: Factors and Multiples
The problem 75 x 5 allows us to explore key mathematical concepts such as factors and multiples.
-
Factors: Factors are numbers that divide evenly into another number without leaving a remainder. The factors of 75 are 1, 3, 5, 15, 25, and 75. The factors of 5 are 1 and 5.
-
Multiples: Multiples are the products obtained by multiplying a number by any integer. The multiples of 75 are 75, 150, 225, 300, 375, and so on. The multiples of 5 are 5, 10, 15, 20, 25, 30, 375, and so on. Notice that 375 is a multiple of both 75 and 5.
Understanding factors and multiples provides a deeper understanding of the relationships between numbers and aids in problem-solving.
V. Extending the Concept: Scaling and Proportionality
75 x 5 can also be viewed within the context of scaling and proportionality. Multiplying 75 by 5 represents a fivefold increase in the original quantity. This concept is fundamental in various fields, including:
-
Map Scaling: Maps often use a scale to represent distances. If a map's scale is 1:75, and a distance on the map measures 5 units, the actual distance is 375 units.
-
Recipe Scaling: Increasing or decreasing recipe sizes involves proportional scaling. Multiplying ingredients by a factor (like 5 in our case) maintains the recipe's proportions.
-
Engineering Design: Scaling designs up or down while maintaining proportions is critical in engineering. This ensures that the scaled version functions correctly.
VI. Beyond the Basics: Prime Factorization and Exponents
Let's analyze 75 and 5 through the lens of prime factorization and exponents:
-
Prime Factorization: Prime factorization involves expressing a number as a product of prime numbers (numbers only divisible by 1 and themselves). The prime factorization of 75 is 3 x 5 x 5 (or 3 x 5²), and the prime factorization of 5 is simply 5.
-
Exponents: Exponents represent repeated multiplication. In the prime factorization of 75, 5² indicates 5 multiplied by itself twice (5 x 5 = 25).
Understanding prime factorization and exponents provides a deeper understanding of number structure and aids in solving more complex mathematical problems.
VII. Connecting to Other Mathematical Concepts
The simple calculation of 75 x 5 serves as a stepping stone to more advanced mathematical concepts:
-
Algebra: The equation 75x = 375 can be solved using algebraic methods to find the value of x (which is 5).
-
Geometry: Calculating areas and volumes often involves multiplication. For example, finding the area of a rectangle with sides of 75 and 5 units.
-
Calculus: While seemingly unrelated, calculus involves concepts of limits and infinitesimals, which build upon a foundational understanding of arithmetic operations like multiplication.
VIII. Frequently Asked Questions (FAQ)
-
What is the easiest way to solve 75 x 5? The easiest method depends on individual preference and mathematical skills. Mental math techniques, the distributive property, or standard multiplication can all be efficient.
-
Why is understanding multiplication important? Multiplication is a fundamental mathematical operation crucial for various applications in everyday life, science, and various professions.
-
How can I improve my multiplication skills? Practice is key! Regularly solving multiplication problems, utilizing different methods, and focusing on mental math techniques will significantly enhance your skills.
-
Are there online resources to help learn multiplication? Yes, numerous online resources, including educational websites and apps, offer interactive multiplication exercises and tutorials.
IX. Conclusion: The Significance of Simplicity
While the calculation 75 x 5 appears simple, it serves as a powerful illustration of fundamental mathematical principles and their widespread applications. By exploring different methods, examining real-world applications, and connecting it to broader mathematical concepts, we gain a deeper appreciation for the power and versatility of even the most basic mathematical operations. The journey from a simple calculation to a deeper understanding of mathematics underscores the value of exploring seemingly simple problems and uncovering the hidden complexities within. This seemingly basic calculation provides a strong foundation for future mathematical exploration and problem-solving. Remember that the key is not just getting the answer (375), but understanding why and how we arrive at that answer. This understanding empowers us to tackle more complex mathematical challenges with confidence and proficiency.
Latest Posts
Latest Posts
-
83 3kg In Stones
Sep 11, 2025
-
1 70m In Feet
Sep 11, 2025
-
197lbs In Kg
Sep 11, 2025
-
63 5kg In Lbs
Sep 11, 2025
-
47 3kg In Stone
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 75 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.