75 X 4
stanleys
Sep 10, 2025 · 6 min read
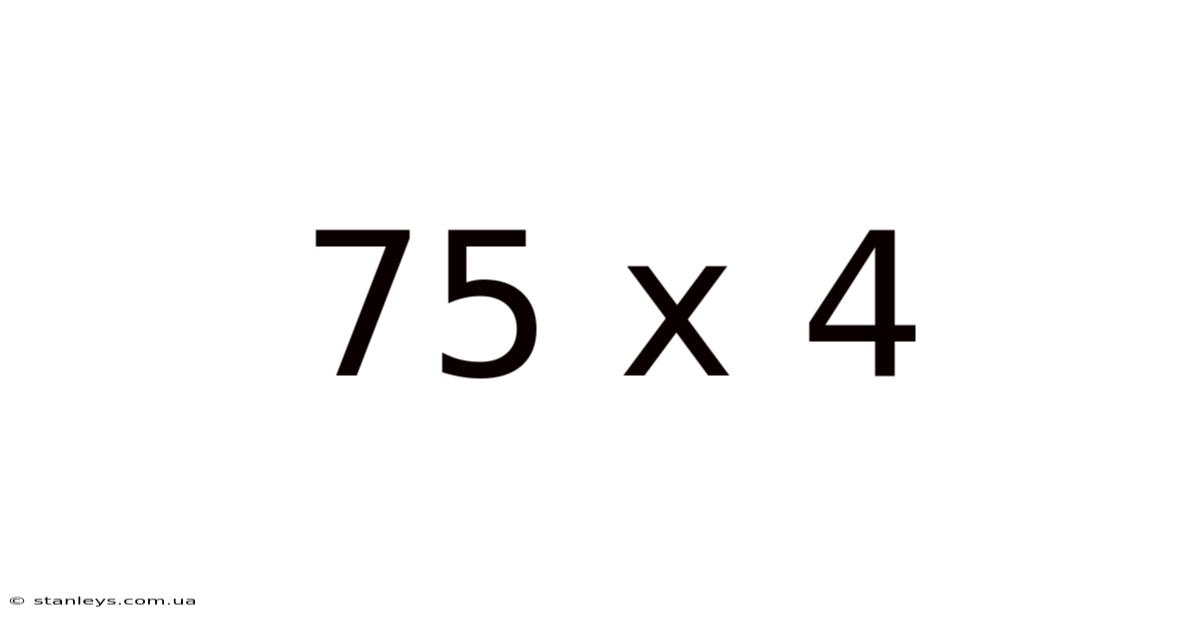
Table of Contents
Unveiling the Mystery: A Deep Dive into 75 x 4
This article explores the seemingly simple calculation of 75 multiplied by 4, delving far beyond the immediate answer. We'll unpack various methods to solve this problem, examining the underlying mathematical principles and exploring real-world applications to illustrate the significance of even basic arithmetic. Understanding multiplication, particularly this seemingly straightforward example, forms the bedrock for more complex mathematical concepts. This exploration will cater to all levels, from elementary school students solidifying their foundational knowledge to adults seeking a refresher or a deeper appreciation of mathematical fundamentals.
Understanding Multiplication: The Building Blocks
Before we dive into 75 x 4, let's reinforce the core concept of multiplication. Multiplication is essentially repeated addition. When we say 75 x 4, we're essentially asking: what is the sum of four 75s? This can be visually represented as:
75 + 75 + 75 + 75 = ?
This approach, while straightforward, becomes cumbersome for larger numbers. Hence, the importance of learning multiplication tables and employing more efficient methods.
Methods for Calculating 75 x 4
Several methods can be used to calculate 75 x 4, each offering different insights into the mathematical process:
1. Standard Multiplication Algorithm:
This is the traditional method taught in schools. We multiply the units digit first, then the tens digit, carrying over any values as needed.
75
x 4
----
300
- Units: 4 x 5 = 20. We write down '0' and carry-over '2'.
- Tens: 4 x 7 = 28. Adding the carried-over '2', we get 30.
Therefore, 75 x 4 = 300.
2. Distributive Property:
The distributive property allows us to break down a multiplication problem into smaller, more manageable parts. We can rewrite 75 as 70 + 5, and then distribute the 4:
4 x (70 + 5) = (4 x 70) + (4 x 5) = 280 + 20 = 300
This method highlights the fundamental properties of arithmetic and can be particularly helpful for larger numbers.
3. Doubling and Halving:
This technique uses repeated doubling and halving to simplify the calculation. We can halve 75 (resulting in 37.5) and double 4 (resulting in 8). While this method leads to a decimal initially, it showcases a different approach: However, this method becomes less practical with odd numbers. Let's use a variation; instead of directly halving 75, we can consider it as 75 = 50 + 25. Now we can easily double 4 and halve 50 and 25:
(8 x 50) + (8 x 25) = 400 + 200 = 600. This is not the result we desire because 50 and 25 are not equivalent to 75 x 2.
While not the most efficient in this case, it demonstrates a flexibility in approaching multiplication problems.
4. Using a Multiplication Table:
For those familiar with multiplication tables, the answer is immediately apparent. The multiplication table of 75, directly shows 4 * 75 = 300. This method relies on memorization and quick recall.
5. Visual Representation:
We can represent 75 x 4 visually using arrays or area models. Imagine a rectangle with a length of 75 units and a width of 4 units. The area of this rectangle represents the product 75 x 4. While not practical for large numbers, this method provides a concrete visualization of multiplication.
Real-World Applications: Beyond the Classroom
The seemingly simple calculation 75 x 4 has numerous applications in various aspects of everyday life. Understanding this calculation is crucial for:
- Shopping: Calculating the total cost of 4 items costing $75 each.
- Measurement: Determining the total length if you have 4 pieces of wood, each measuring 75 centimeters.
- Cooking: Calculating the amount of ingredients needed if a recipe calls for 75 grams of something, and you need to make 4 times the recipe.
- Finance: Calculating the total earnings from 4 hours of work at a rate of $75 per hour.
- Construction: Calculating the number of bricks needed if each row requires 75 bricks and you have 4 rows.
These examples demonstrate how fundamental arithmetic permeates our daily activities. Mastering basic calculations like 75 x 4 provides a solid foundation for tackling more complex mathematical challenges in various fields.
Expanding the Understanding: Moving Beyond 75 x 4
The principle of multiplication extends far beyond this single example. Understanding how to calculate 75 x 4 allows you to approach more complex calculations with confidence. For instance:
- Multiplying by multiples of 4: Once you understand 75 x 4, you can easily calculate 75 x 8 (double the result), 75 x 12 (triple the result), and so on.
- Multiplying larger numbers: By breaking down larger numbers into smaller components (using the distributive property) and applying the same principles, you can effectively solve more complex multiplication problems.
- Working with fractions and decimals: The same fundamental principles apply when working with fractions and decimals. Understanding the core concept of multiplication ensures a smoother transition to these more advanced concepts.
The ability to perform accurate and efficient calculations is a vital life skill, applicable in various professional and personal contexts.
Frequently Asked Questions (FAQs)
Q1: What is the quickest way to calculate 75 x 4?
A1: The quickest way is to use the standard multiplication algorithm or recall the answer from a multiplication table if memorized.
Q2: Why is it important to learn different methods of multiplication?
A2: Learning different methods provides a deeper understanding of the underlying mathematical principles. It also helps to develop problem-solving skills and find the most efficient approach for different situations.
Q3: How can I improve my multiplication skills?
A3: Practice regularly, use various methods, and try solving real-world problems that involve multiplication. Consider using online resources, games, and worksheets to enhance learning.
Q4: What if I encounter a more complex multiplication problem?
A4: Break down the problem into smaller, more manageable parts, and apply the fundamental principles of multiplication. Remember that complex problems are simply combinations of simpler operations.
Q5: Can I use a calculator?
A5: While calculators are useful tools, understanding the underlying mathematical principles is essential for developing a strong foundation in mathematics. Calculators should be used as a verification tool, rather than a replacement for understanding the process.
Conclusion: The Enduring Importance of Basic Arithmetic
While the calculation 75 x 4 may seem trivial at first glance, it represents a fundamental building block in mathematics. Understanding the various methods to solve this simple problem, and more importantly, grasping the underlying mathematical principles, is crucial for developing strong mathematical skills. These skills extend far beyond the classroom, impacting various aspects of our personal and professional lives. The ability to perform accurate calculations efficiently is a valuable asset, contributing to success in numerous fields. So, the next time you encounter a seemingly simple multiplication problem, remember the depth of understanding it can unlock. The journey from 75 x 4 to mastering more complex calculations is a testament to the power of consistent learning and exploration.
Latest Posts
Latest Posts
-
7 5cm In Mm
Sep 10, 2025
-
Special Experience Identifier
Sep 10, 2025
-
Kiss Kate Barlow
Sep 10, 2025
-
58 3kg In Stones
Sep 10, 2025
-
57 4kg In Stone
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 75 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.