75 Of 48
stanleys
Sep 14, 2025 · 5 min read
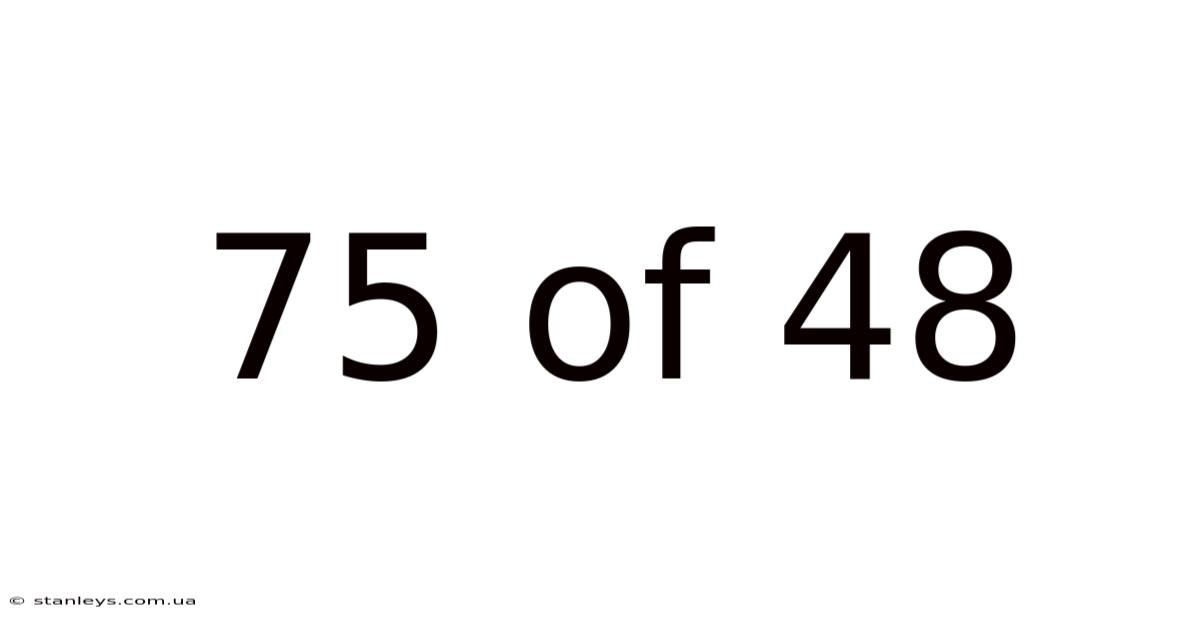
Table of Contents
Decoding 75/48: Understanding Fractions, Ratios, and Their Applications
Understanding fractions and ratios is fundamental to mathematics and numerous real-world applications. This article delves into the meaning of 75/48, explaining how to simplify it, its representation as a decimal and percentage, and explores its practical uses across various fields. We’ll also address common misconceptions and provide helpful tips for working with fractions and ratios. This comprehensive guide aims to build a solid understanding, empowering you to confidently tackle similar problems in the future.
Understanding Fractions: A Refresher
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. In the fraction 75/48, 75 is the numerator and 48 is the denominator. This means we are considering 75 parts out of a total of 48 parts. Notice that the numerator is larger than the denominator; this signifies an improper fraction, representing a value greater than one.
Simplifying the Fraction 75/48
Improper fractions are often simplified into mixed numbers or reduced to their lowest terms. Simplifying a fraction means finding an equivalent fraction where the numerator and denominator are smaller, but the fraction's value remains the same. This is achieved by finding the greatest common divisor (GCD) of both the numerator and denominator and dividing both by it.
Let's find the GCD of 75 and 48. We can use prime factorization:
- 75 = 3 x 5 x 5
- 48 = 2 x 2 x 2 x 2 x 3
The common factor is 3. Dividing both the numerator and denominator by 3, we get:
75 ÷ 3 = 25 48 ÷ 3 = 16
Therefore, the simplified fraction is 25/16.
Converting to Mixed Number and Decimal
The simplified improper fraction 25/16 can be converted into a mixed number. This involves dividing the numerator by the denominator:
25 ÷ 16 = 1 with a remainder of 9
The quotient (1) becomes the whole number part, and the remainder (9) becomes the numerator of the fractional part, keeping the same denominator (16). Thus, 25/16 as a mixed number is 1 9/16.
To convert the fraction to a decimal, we perform the division:
25 ÷ 16 = 1.5625
Therefore, 75/48 is equal to 1.5625 as a decimal.
Converting to Percentage
A percentage represents a fraction out of 100. To convert the decimal 1.5625 to a percentage, we multiply by 100:
1.5625 x 100 = 156.25%
So, 75/48 is equal to 156.25%.
Ratios: Understanding the Relationship
While 75/48 is a fraction, it also represents a ratio. A ratio shows the relative size of two or more values. In this case, the ratio is 75:48, indicating a relationship between two quantities. Just like fractions, ratios can be simplified by dividing both numbers by their greatest common divisor (in this case, 3), resulting in a simplified ratio of 25:16. This means for every 25 units of one quantity, there are 16 units of another.
Real-World Applications of Fractions and Ratios
Fractions and ratios are ubiquitous in everyday life and various professions. Here are a few examples:
- Cooking: Recipes often use fractions (e.g., 1/2 cup of sugar, 2/3 cup of flour).
- Construction: Ratios are crucial in mixing concrete and other building materials. The precise ratio of cement, sand, and gravel determines the strength and quality of the concrete.
- Finance: Calculating interest rates, profits, and losses often involves working with fractions and percentages.
- Engineering: Design specifications for machinery and structures commonly involve ratios and fractions to ensure precise dimensions and functionality.
- Science: In chemistry, stoichiometry heavily relies on ratios to determine the amounts of reactants and products in chemical reactions.
- Data Analysis: Percentages and fractions are essential for interpreting data, calculating statistics, and presenting findings.
Advanced Concepts: Proportionality and Problem Solving
Understanding proportionality is vital when dealing with fractions and ratios. Proportions state that two ratios are equal. This concept is fundamental in solving problems involving scaling, conversions, and similar triangles. For example, if we know that the ratio of boys to girls in a class is 25:16, and there are 25 boys, we can use proportionality to find the number of girls:
25/16 = 25/x (where x is the number of girls)
Solving for x, we find x = 16. This means there are 16 girls in the class.
Common Mistakes and How to Avoid Them
Several common errors occur when working with fractions and ratios:
- Incorrect simplification: Failing to find the greatest common divisor leads to incomplete simplification.
- Improper conversion: Mistakes in converting between fractions, decimals, and percentages are frequent.
- Incorrect ratio interpretation: Misunderstanding the relationship between the quantities represented by a ratio can lead to incorrect calculations.
- Errors in solving proportions: Setting up or solving proportions incorrectly can lead to inaccurate results.
To avoid these mistakes, practice regularly, double-check your calculations, and use different methods to verify your answers.
Frequently Asked Questions (FAQ)
Q: Can a ratio be expressed as a fraction?
A: Yes, a ratio can always be expressed as a fraction. The two numbers in the ratio become the numerator and denominator of the fraction.
Q: What if the denominator of a fraction is zero?
A: A fraction cannot have a denominator of zero. Division by zero is undefined in mathematics.
Q: How do I compare two fractions?
A: To compare two fractions, find a common denominator and compare the numerators. Alternatively, convert the fractions to decimals and compare the decimal values.
Q: What's the difference between a ratio and a fraction?
A: While often interchangeable in numerical representation, a fraction represents a part of a whole, whereas a ratio compares two or more quantities. A fraction usually implies a part-to-whole relationship, while a ratio can describe any comparison of quantities.
Conclusion
Understanding fractions and ratios is crucial for success in mathematics and various real-world applications. This article provided a comprehensive explanation of the fraction 75/48, covering its simplification, conversion to decimals and percentages, its representation as a ratio, and its practical relevance. By mastering these fundamental concepts and avoiding common mistakes, you will be equipped to confidently tackle a wide range of problems involving fractions and ratios, building a strong foundation for advanced mathematical studies and problem-solving skills. Remember to practice regularly and seek clarification when needed to solidify your understanding.
Latest Posts
Latest Posts
-
95 9kg In Stones
Sep 14, 2025
-
83 Km Miles
Sep 14, 2025
-
Factors Influence Supply
Sep 14, 2025
-
Lt To Lbs
Sep 14, 2025
-
3 15 Simplified
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.