70 Of 35
stanleys
Sep 13, 2025 · 6 min read
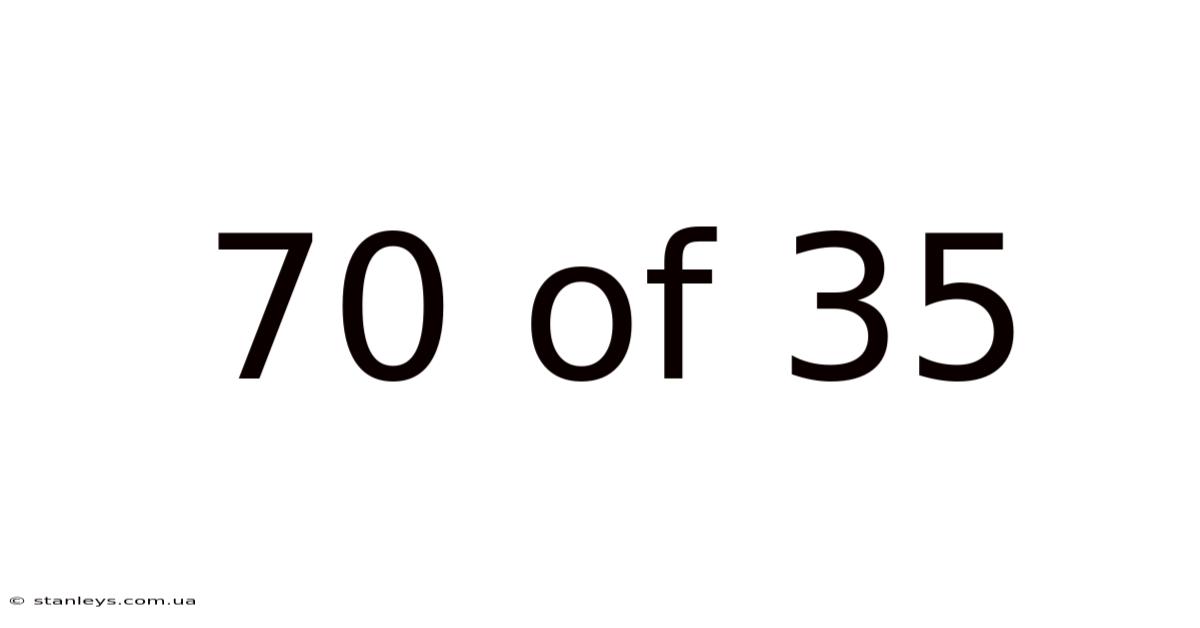
Table of Contents
Decoding the Fraction: Understanding 70/35 and its Implications
Understanding fractions is a fundamental building block in mathematics, crucial for everyday life and advanced studies alike. This article dives deep into the seemingly simple fraction 70/35, exploring its simplification, practical applications, and the broader mathematical concepts it illustrates. We'll unravel the mystery behind this fraction, equipping you with a solid understanding of how to handle similar fractions and appreciate the elegance of mathematical reasoning.
Introduction: What Does 70/35 Represent?
The fraction 70/35 represents a part-to-whole relationship. The number 70 is the numerator, representing the number of parts we're considering, while 35 is the denominator, representing the total number of equal parts that make up the whole. In simpler terms, imagine you have a pizza cut into 35 equal slices. The fraction 70/35 indicates you possess 70 of these slices. This immediately suggests something interesting: you have more slices than the entire pizza. This leads us to the crucial process of simplification.
Simplifying the Fraction: Finding the Lowest Terms
The fraction 70/35 is an improper fraction because the numerator is larger than the denominator. To understand its true value, we need to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator and denominator and dividing both by it.
The GCD of 70 and 35 is 35. This is because 35 is a factor of 70 (70 = 35 x 2). Dividing both the numerator and the denominator by 35, we get:
70 ÷ 35 = 2 35 ÷ 35 = 1
Therefore, the simplified form of 70/35 is 2/1, which is simply equal to 2. This means that 70/35 represents the whole number 2.
Practical Applications: Real-World Examples
The concept of simplifying fractions like 70/35 has numerous real-world applications. Consider these scenarios:
-
Baking: A recipe calls for 35 grams of flour per serving. If you want to make a double batch (70 grams of flour), the fraction 70/35 directly represents the scaling factor – you need twice the amount of flour.
-
Measurement: Imagine measuring a length. If a specific unit of measurement is 35 centimeters, and you need a length of 70 centimeters, the fraction 70/35 shows you need twice the unit.
-
Financial Calculations: If you earn 35 dollars per hour, and you worked for 2 hours (70 dollars earned), the fraction 70/35 illustrates your hourly rate.
-
Ratio and Proportion: Fractions represent ratios. The ratio 70:35 simplifies to 2:1, indicating a ratio of 2 to 1.
Beyond the Basics: Exploring Equivalent Fractions
While 2 is the simplified form of 70/35, there are infinitely many equivalent fractions representing the same value. An equivalent fraction is obtained by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For instance:
- Multiplying both 70 and 35 by 2 gives 140/70, which simplifies to 2.
- Multiplying both 70 and 35 by 3 gives 210/105, which also simplifies to 2.
Understanding equivalent fractions is vital for comparing and manipulating fractions effectively.
Understanding Improper Fractions and Mixed Numbers
As mentioned earlier, 70/35 is an improper fraction – the numerator is greater than the denominator. Improper fractions can be converted into mixed numbers. A mixed number combines a whole number and a proper fraction.
To convert 70/35 to a mixed number, we perform the division: 70 ÷ 35 = 2. Since the division results in a whole number with no remainder, the mixed number representation is simply 2. If there was a remainder, the remainder would become the numerator of the proper fraction part of the mixed number, with the denominator remaining the same as the original improper fraction.
The Role of Divisibility Rules in Simplification
Efficiently simplifying fractions relies on understanding divisibility rules. Divisibility rules provide quick ways to determine if a number is divisible by another number without performing long division. For example:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, 8).
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
Using these rules, we quickly see that both 70 and 35 are divisible by 5. Further investigation reveals that both are divisible by 35, leading to the simplified form of 2.
Connecting to Larger Mathematical Concepts
The seemingly simple fraction 70/35 connects to several broader mathematical concepts:
-
Ratio and Proportion: As discussed earlier, fractions represent ratios, which are essential in understanding proportions and solving related problems.
-
Algebra: Fractions are fundamental in algebraic manipulations, solving equations, and working with variables.
-
Calculus: Fractions and their properties are essential building blocks in calculus, particularly in dealing with derivatives and integrals.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 70/35?
A: The simplest form of 70/35 is 2.
Q: Is 70/35 a proper or improper fraction?
A: 70/35 is an improper fraction because the numerator (70) is greater than the denominator (35).
Q: How do I convert an improper fraction to a mixed number?
A: Divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number. The remainder (if any) becomes the numerator of the fractional part, with the denominator remaining the same. In the case of 70/35, there is no remainder, resulting in the whole number 2.
Q: What are equivalent fractions?
A: Equivalent fractions represent the same value but have different numerators and denominators. They are obtained by multiplying or dividing both the numerator and the denominator by the same non-zero number.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It provides a clearer representation of the part-to-whole relationship and simplifies further calculations.
Conclusion: The Power of Simplification
The seemingly simple fraction 70/35 offers a powerful illustration of fundamental mathematical concepts. Through simplification, we unveil its true value of 2, highlighting the importance of understanding equivalent fractions, improper fractions, and the application of divisibility rules. This exploration extends beyond basic arithmetic, laying the foundation for more complex mathematical concepts encountered in higher-level studies and numerous real-world applications. Mastering the manipulation of fractions is not just about solving equations; it’s about developing a deeper understanding of numerical relationships and their practical significance. The journey of understanding 70/35 is a microcosm of the elegance and power of mathematical reasoning.
Latest Posts
Latest Posts
-
83 3kg To Lbs
Sep 13, 2025
-
48 4
Sep 13, 2025
-
55lb In Kg
Sep 13, 2025
-
50 X 7
Sep 13, 2025
-
Ng To Grams
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.