70 Of 176
stanleys
Sep 14, 2025 · 5 min read
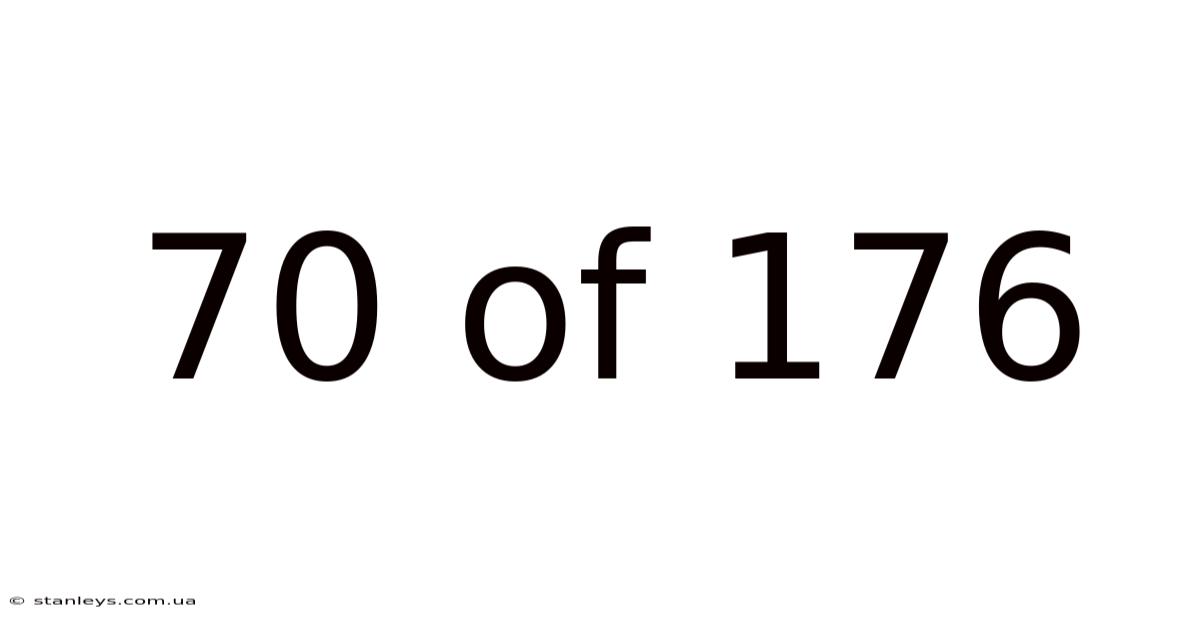
Table of Contents
Decoding the Fraction: Understanding 70/176 and its Implications
The fraction 70/176, seemingly simple at first glance, offers a rich opportunity to explore various mathematical concepts. Understanding this fraction involves not just simplifying it to its lowest terms, but also delving into its decimal representation, percentage equivalent, and its applications in real-world scenarios. This comprehensive guide will navigate you through these concepts, equipping you with a deeper understanding of fractions and their importance in mathematics and beyond.
Introduction: The Basics of Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In 70/176, 70 is the numerator and 176 is the denominator. This means we have 70 parts out of a total of 176 equal parts.
Understanding fractions is fundamental to numerous areas, including:
- Everyday life: Dividing a pizza, sharing resources, measuring ingredients in recipes.
- Mathematics: Foundation for more advanced concepts like algebra, calculus, and probability.
- Science: Expressing proportions, ratios, and measurements in various scientific fields.
- Engineering: Calculations involving proportions, scaling, and measurements.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve deeper, simplifying the fraction 70/176 makes it easier to work with. This involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
To find the GCD of 70 and 176, we can use the Euclidean algorithm:
- Divide the larger number (176) by the smaller number (70): 176 ÷ 70 = 2 with a remainder of 36.
- Replace the larger number with the remainder (36) and repeat: 70 ÷ 36 = 1 with a remainder of 34.
- Continue the process: 36 ÷ 34 = 1 with a remainder of 2.
- Repeat until the remainder is 0: 34 ÷ 2 = 17 with a remainder of 0.
The last non-zero remainder is the GCD, which is 2.
Now we can simplify the fraction by dividing both the numerator and the denominator by the GCD:
70 ÷ 2 = 35 176 ÷ 2 = 88
Therefore, the simplified fraction is 35/88.
Converting to Decimal: Understanding the Decimal Equivalent
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. Using a calculator or long division:
35 ÷ 88 ≈ 0.3977
Therefore, the decimal equivalent of 70/176 (or 35/88) is approximately 0.3977. Note that this is an approximation because the decimal representation is non-terminating (it doesn't end) and recurring (it has a repeating pattern).
Expressing as a Percentage: Percentage Representation
To express the fraction as a percentage, we multiply the decimal equivalent by 100:
0.3977 × 100 ≈ 39.77%
So, 70/176 is approximately 39.77%. This means that 70 represents approximately 39.77% of 176.
Real-World Applications: Illustrative Examples
The fraction 70/176, or its simplified form 35/88, can represent various real-world situations:
- Survey Results: If 70 out of 176 people surveyed preferred a particular product, then 35/88 or approximately 39.77% preferred that product.
- Test Scores: If a student answered 70 questions correctly out of a total of 176 questions, their score would be 35/88 or about 39.77%.
- Resource Allocation: If 70 units of a resource are allocated from a total of 176 units, this represents 35/88 or approximately 39.77% of the total resource.
- Probability: If an event has a probability of 70/176, it means there's a 39.77% chance of the event occurring.
Further Mathematical Explorations: Beyond Simplification
Beyond simplification, the fraction 70/176 opens avenues for exploring other mathematical concepts:
- Ratio and Proportion: The fraction establishes a ratio between two quantities. This ratio can be used to solve problems involving proportions. For example, if we know that 70 units cost $x, we can use the ratio to find the cost of 176 units.
- Percentage Change: The fraction can be used to calculate percentage increases or decreases. If the initial value is 176 and it decreases to 70, the percentage decrease can be calculated using the fraction.
- Conversion to Other Forms: The fraction can be converted to other forms like mixed numbers (which would be 0 and 35/88) or expressed using different units depending on the context.
Frequently Asked Questions (FAQ)
Q: Is 70/176 in its simplest form?
A: No, 70/176 can be simplified to 35/88 by dividing both the numerator and denominator by their greatest common divisor, which is 2.
Q: How do I convert 70/176 to a percentage without using a calculator?
A: You can first simplify the fraction to 35/88. Then, perform long division to get the decimal equivalent. Finally, multiply the decimal by 100 to get the percentage.
Q: What are some real-world examples where I might encounter this fraction or similar fractions?
A: Many scenarios involve fractions representing parts of a whole, such as survey results, test scores, resource allocation, and probability calculations. Any situation involving ratios and proportions could be represented by a fraction.
Q: Is there a way to visualize this fraction?
A: Yes, you could represent 70/176 using a pie chart, a bar graph, or other visual aids to demonstrate the proportion of 70 parts out of 176 equal parts. You could also divide a shape into 176 equal parts and shade 70 of them.
Q: What are the limitations of using approximations when working with fractions?
A: Approximations can lead to slight inaccuracies in calculations, especially when dealing with sensitive data or high-precision calculations. In some applications, using the exact fraction (or its simplified form) is crucial to ensure accuracy.
Conclusion: The Significance of Fractional Understanding
The seemingly simple fraction 70/176 provides a gateway to understanding fundamental mathematical concepts. By simplifying, converting to decimal and percentage forms, and exploring its real-world applications, we gain a deeper appreciation of fractions and their importance in various fields. This comprehensive analysis highlights the importance of mastering fractions, not just for academic success but also for navigating everyday situations and solving real-world problems with precision and accuracy. Remember that a thorough understanding of fractions forms a strong foundation for more advanced mathematical concepts and problem-solving skills.
Latest Posts
Latest Posts
-
Hayden Planetarium Manhattan
Sep 14, 2025
-
120ml In Oz
Sep 14, 2025
-
Katelyn Ohashi Olympics
Sep 14, 2025
-
58 2kg In Stone
Sep 14, 2025
-
70ml In Grams
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 176 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.