70 Of 120
stanleys
Sep 11, 2025 · 6 min read
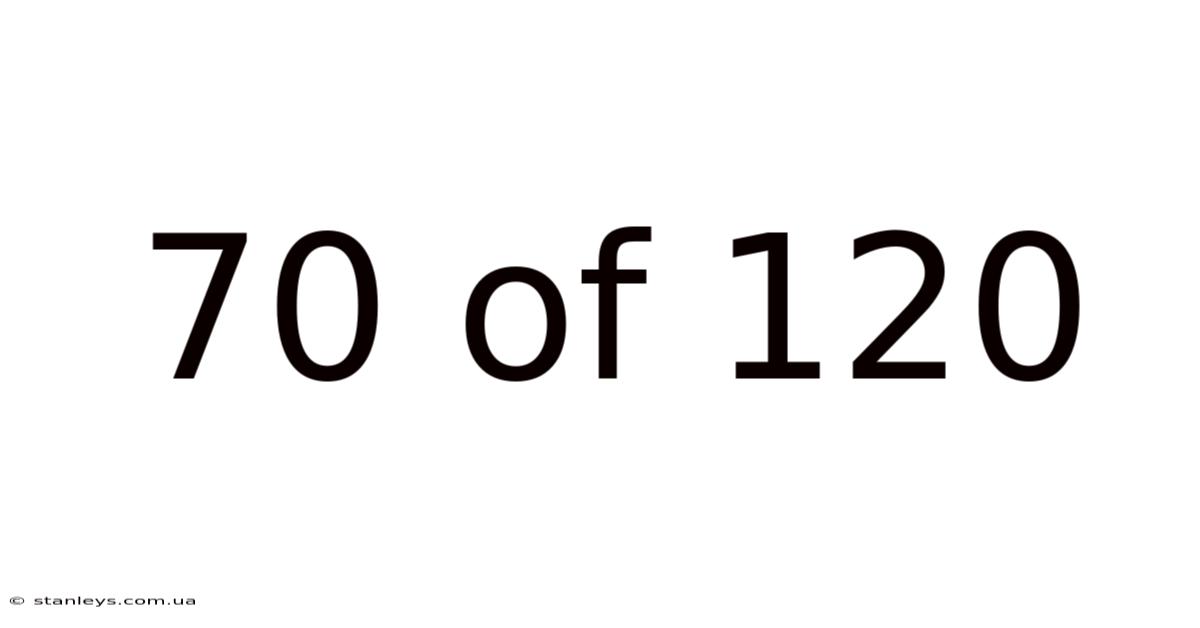
Table of Contents
Decoding the Fraction 70/120: A Comprehensive Guide to Understanding, Simplifying, and Applying Fractions
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in daily life and advanced studies. This article delves into the specific fraction 70/120, providing a comprehensive guide to its simplification, interpretation, and practical uses. We'll explore its representation in different contexts, including decimal form, percentage, and its application in real-world problems. This deep dive will equip you with a solid understanding of this seemingly simple fraction and enhance your overall fractional literacy.
Introduction: What is 70/120?
The fraction 70/120 represents a part of a whole. The numerator (70) indicates the number of parts we are considering, while the denominator (120) represents the total number of equal parts that make up the whole. This means 70 out of 120 parts are being considered. At first glance, it might seem like a complex fraction, but with the right approach, we can simplify it and understand its meaning much better. This article will guide you through this process step by step.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we can fully grasp the meaning of 70/120, it's essential to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both 70 and 120 without leaving a remainder.
One way to find the GCD is through prime factorization. Let's break down both numbers:
- 70: 2 x 5 x 7
- 120: 2 x 2 x 2 x 3 x 5
The common prime factors are 2 and 5. Therefore, the GCD is 2 x 5 = 10.
Now, we divide both the numerator and the denominator by the GCD:
70 ÷ 10 = 7 120 ÷ 10 = 12
Therefore, the simplified fraction is 7/12. This simplified form is much easier to work with and represents the same value as 70/120.
Representing 70/120 in Different Forms
Understanding a fraction isn't limited to its fractional form. We can also represent it as a decimal, a percentage, and even visually.
Decimal Representation
To convert 7/12 (the simplified form) into a decimal, we divide the numerator by the denominator:
7 ÷ 12 ≈ 0.58333...
The decimal representation is a recurring decimal, meaning the digit 3 repeats infinitely. For practical purposes, we often round it off to a certain number of decimal places, for example, 0.58 or 0.583.
Percentage Representation
To express 7/12 as a percentage, we multiply the decimal representation by 100:
0.58333... x 100 ≈ 58.33%
This means 7/12 represents approximately 58.33% of the whole.
Visual Representation
We can visually represent 7/12 using a diagram. Imagine a shape divided into 12 equal parts. Shading 7 of those parts would visually represent the fraction 7/12. This helps to understand the concept of parts of a whole in a concrete way.
Real-World Applications of 70/120 (and 7/12)
Fractions are ubiquitous in everyday life. Let's look at some examples where understanding 70/120, or its simplified form 7/12, could be useful:
-
Baking: If a recipe calls for 12 cups of flour and you only want to make 7/12 of the recipe, you would need 7 cups of flour.
-
Surveys and Statistics: If 70 out of 120 people surveyed preferred a particular product, the fraction 70/120 (or 7/12) represents the proportion of people who preferred that product. This can be easily converted to a percentage (approximately 58.33%) for easier interpretation.
-
Geometry and Measurement: Imagine a pizza cut into 12 slices. Eating 7 slices would mean you consumed 7/12 of the pizza.
-
Project Management: If a project has 12 tasks, and 7 are completed, the fraction 7/12 represents the progress made.
-
Financial Calculations: Fractions are essential for understanding interest rates, discounts, and other financial concepts. For example, a 7/12 discount on an item means a discount of approximately 58.33% of the original price.
Understanding the Concept of Ratio
The fraction 70/120 can also be interpreted as a ratio. A ratio compares two quantities. In this case, the ratio is 70:120, which simplifies to 7:12. This means for every 7 parts of one quantity, there are 12 parts of another quantity. This ratio representation is frequently used in various fields, including scaling, mixing ingredients, and comparing different datasets.
Further Exploration: Working with Fractions
Mastering fractions requires understanding various operations:
-
Addition and Subtraction: Adding or subtracting fractions requires a common denominator. For example, adding 7/12 and 2/12 would result in 9/12, which can be further simplified to 3/4.
-
Multiplication: Multiplying fractions involves multiplying the numerators together and the denominators together. For example, 7/12 multiplied by 2/3 would be (7 x 2) / (12 x 3) = 14/36, which simplifies to 7/18.
-
Division: Dividing fractions involves inverting the second fraction and multiplying. For example, 7/12 divided by 2/3 would be 7/12 x 3/2 = 21/24, which simplifies to 7/8.
Frequently Asked Questions (FAQ)
Q: Can I simplify 70/120 directly without finding the GCD?
A: While you can simplify by dividing by common factors repeatedly (e.g., dividing by 2, then by 5), finding the GCD ensures you simplify to the lowest terms in the fewest steps.
Q: What if I round the decimal representation of 7/12 differently?
A: Rounding affects precision. Using more decimal places offers greater accuracy, but for many applications, rounding to a few decimal places is sufficient.
Q: Are there other methods to find the GCD?
A: Yes, the Euclidean algorithm is another efficient method for finding the greatest common divisor of two numbers.
Q: How can I practice working with fractions?
A: Practice is key! Solve various problems involving fractions, including addition, subtraction, multiplication, and division. Online resources and textbooks offer numerous practice exercises.
Conclusion: Mastering Fractions, One Step at a Time
The fraction 70/120, simplified to 7/12, is more than just a mathematical concept. It's a tool for understanding proportions, ratios, and percentages in various real-world scenarios. This article provided a detailed explanation of its simplification, representation in different forms, and its practical applications. By understanding the fundamental principles of fractions, you gain a crucial skill applicable across numerous academic disciplines and everyday life situations. Remember that consistent practice and a grasp of the underlying concepts are essential to mastering this fundamental aspect of mathematics. Continue exploring different fractional problems and deepen your understanding to unlock a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Brother In Land
Sep 12, 2025
-
Anglo Saxon Photos
Sep 12, 2025
-
330ml In L
Sep 12, 2025
-
32cm To Mm
Sep 12, 2025
-
65 Of 60
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.