7/15 X 360
stanleys
Sep 16, 2025 · 5 min read
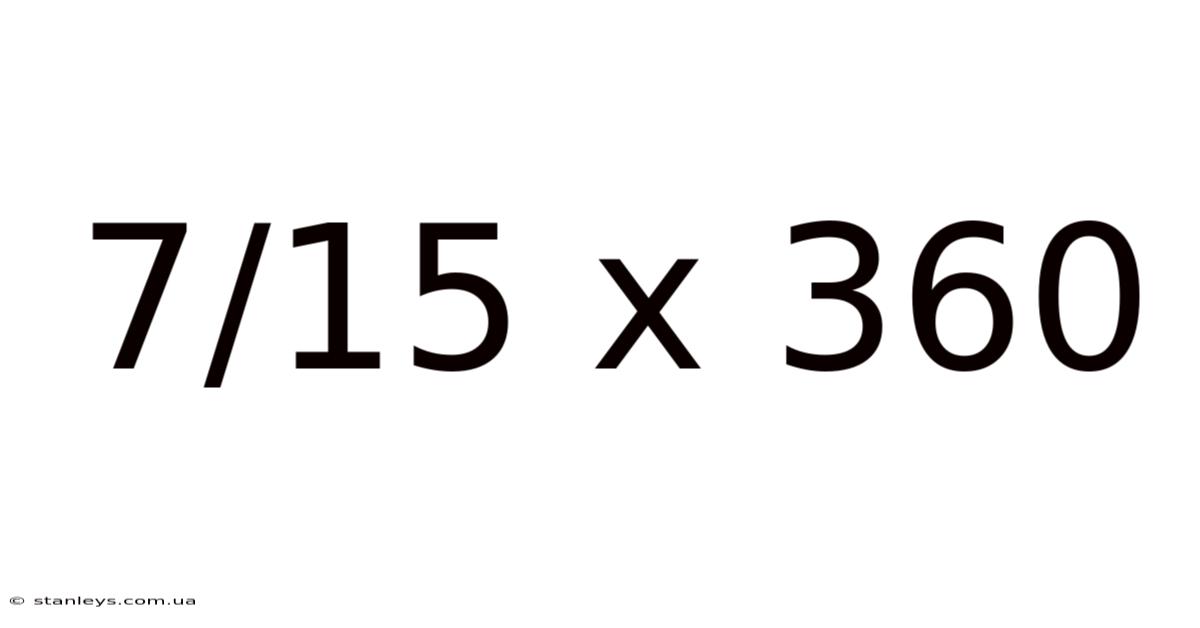
Table of Contents
Decoding 7/15 x 360: A Deep Dive into Fractions, Multiplication, and Real-World Applications
This article will explore the seemingly simple mathematical problem of 7/15 x 360, providing a comprehensive explanation that goes beyond just finding the answer. We'll dissect the process, explain the underlying principles of fraction multiplication, and delve into real-world scenarios where such calculations are frequently applied. This will equip you with a solid understanding not only of this specific problem but also of the broader mathematical concepts involved. Understanding fraction multiplication is a cornerstone of many areas, from basic arithmetic to advanced calculus.
Understanding the Problem: 7/15 x 360
At first glance, 7/15 x 360 might seem daunting, especially for those who haven't worked extensively with fractions. However, breaking down the problem into smaller, manageable steps makes the process straightforward. The core concept is multiplying a fraction (7/15) by a whole number (360). The result will be a number that represents a fractional part of 360.
Method 1: Simplifying Before Multiplying
This method emphasizes efficiency. Before embarking on the multiplication, we can simplify the calculation by canceling common factors between the numerator (7) and the denominator (15) and the whole number (360).
-
Identify Common Factors: The number 360 is divisible by 15. Let's perform the division: 360 / 15 = 24.
-
Rewrite the Equation: We can now rewrite the equation as: (7/15) x (15 x 24) = 7 x 24. Notice how the 15 in the denominator cancels out with the 15 in the factored 360.
-
Perform the Multiplication: Now, we simply multiply 7 by 24: 7 x 24 = 168.
Therefore, 7/15 x 360 = 168. This method demonstrates the power of simplification in making complex calculations much easier. It's a crucial technique for tackling more complex fraction problems.
Method 2: Direct Multiplication and Simplification
This method involves multiplying the numerator by the whole number, and then simplifying the resulting fraction.
-
Multiply the Numerator by the Whole Number: Multiply the numerator of the fraction (7) by the whole number (360): 7 x 360 = 2520.
-
Form the New Fraction: This gives us the improper fraction 2520/15.
-
Simplify the Fraction: Now, we simplify this fraction by finding the greatest common divisor (GCD) of 2520 and 15. The GCD of 2520 and 15 is 15. Divide both the numerator and denominator by 15: 2520 / 15 = 168 and 15 / 15 = 1.
Therefore, the simplified fraction is 168/1, which simplifies to 168.
This method, while slightly longer, provides a clearer understanding of the process of fraction multiplication and simplification. It's useful for demonstrating the fundamental principles involved.
Understanding Fraction Multiplication: A Deeper Dive
To fully grasp the solution, let's delve into the fundamental principles governing fraction multiplication. When multiplying fractions, we simply multiply the numerators together and the denominators together. This is easily represented as: (a/b) x (c/d) = (a x c) / (b x d).
In our example, 7/15 x 360 can be rewritten as (7/15) x (360/1). Following the rule, we get (7 x 360) / (15 x 1) = 2520/15. Simplifying this improper fraction (as shown in Method 2) leads us to the final answer of 168.
Real-World Applications of Fraction Multiplication
Fraction multiplication is surprisingly prevalent in everyday life, showing up in various scenarios:
-
Cooking and Baking: Recipes often require fractional measurements. Scaling a recipe up or down involves fraction multiplication. For example, if a recipe calls for 1/2 cup of sugar and you want to double the recipe, you'd calculate 1/2 x 2 = 1 cup.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Calculating material quantities, dimensions, and proportions frequently involves fraction multiplication.
-
Finance and Budgeting: Calculating percentages, discounts, and interest often uses fractions. For example, determining 7/15 of a $360 budget translates directly to this problem's calculation.
-
Data Analysis: In statistics and data analysis, dealing with proportions and percentages is common. These proportions are represented as fractions and often involve multiplication.
-
Geometry and Measurement: Calculating areas, volumes, and other geometric properties often involves multiplying fractions, particularly when dealing with complex shapes or scales.
Frequently Asked Questions (FAQ)
-
Why is it important to simplify fractions? Simplifying fractions makes calculations easier and reduces the risk of errors. Working with smaller numbers is often less cumbersome.
-
Can I use a calculator to solve this problem? Yes, you can. Most calculators can handle fraction multiplication. However, understanding the underlying principles remains crucial for problem-solving in more complex scenarios.
-
What if the fraction and the whole number had a common factor that wasn’t easily visible? Finding the Greatest Common Divisor (GCD) using prime factorization or the Euclidean algorithm would help find the common factor for simplifying the fraction.
-
What if the problem involved more than one fraction? The process extends naturally; multiply all numerators together, then all denominators, and then simplify the resulting fraction.
-
Are there other methods to solve this problem? Yes, you could convert the fraction into a decimal (7/15 ≈ 0.4667) and then multiply by 360. However, this approach may introduce rounding errors, leading to a less precise answer compared to the methods described above.
Conclusion: Mastering Fraction Multiplication
Solving 7/15 x 360 demonstrates the practical application of fraction multiplication. While the solution itself (168) is straightforward, the underlying concepts are valuable. By understanding both the direct multiplication and the simplification methods, you gain a deeper appreciation for working with fractions. This understanding transcends simple arithmetic, providing a strong foundation for more advanced mathematical concepts and real-world problem-solving across various fields. Remember, the key is not just getting the right answer but also understanding why it's the right answer and how this specific problem relates to broader mathematical principles. The more you practice, the more comfortable and proficient you'll become in handling fractions and their applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7/15 X 360 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.