6x 4 Factorise
stanleys
Sep 14, 2025 · 5 min read
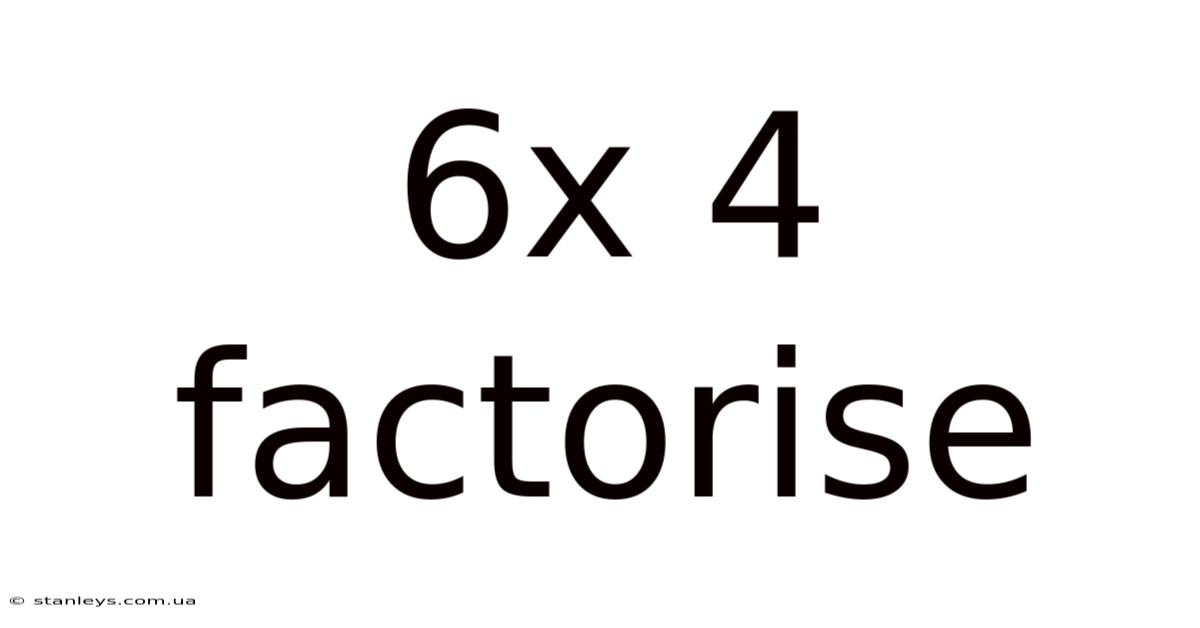
Table of Contents
Mastering 6x + 4 Factorisation: A Comprehensive Guide
Factoring expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding more advanced mathematical concepts. This comprehensive guide delves into the process of factorising the expression 6x + 4, exploring different methods, providing detailed explanations, and addressing frequently asked questions. We'll move beyond a simple answer, equipping you with a deeper understanding of the underlying principles and broader applications.
Introduction to Factorisation
Factorisation, in its simplest form, involves breaking down a mathematical expression into smaller, simpler expressions that, when multiplied together, produce the original expression. Think of it like reverse multiplication. For instance, the factored form of 12 is 2 x 2 x 3, because multiplying those three numbers together gives you 12. Similarly, factoring algebraic expressions like 6x + 4 involves finding common factors and rewriting the expression as a product of those factors.
Step-by-Step Factorisation of 6x + 4
The key to factorising 6x + 4 lies in identifying the greatest common factor (GCF) of the terms 6x and 4. Let's break down the process step-by-step:
Step 1: Find the GCF
First, find the greatest common factor of the coefficients (the numbers in front of the variables). The coefficients are 6 and 4. The factors of 6 are 1, 2, 3, and 6. The factors of 4 are 1, 2, and 4. The greatest number that divides both 6 and 4 evenly is 2.
Step 2: Identify Common Variables
Next, examine the variables. The first term, 6x, contains the variable 'x', while the second term, 4, does not. This means there are no common variables between the two terms.
Step 3: Factor Out the GCF
Now that we've identified the GCF as 2, we factor it out from both terms:
6x + 4 = 2(3x) + 2(2)
Notice that we've divided each term by the GCF (2) and placed the resulting expressions inside the parentheses.
Step 4: Simplify the Expression
Finally, we can rewrite the expression in its factored form by combining the GCF with the expressions inside the parentheses:
6x + 4 = 2(3x + 2)
This is the fully factored form of the expression 6x + 4. This means that if you were to expand 2(3x + 2) using the distributive property (multiplying 2 by both terms inside the parentheses), you would get back to the original expression, 6x + 4.
Understanding the Underlying Principles
The method used above relies on the distributive property of multiplication. The distributive property states that a(b + c) = ab + ac. In our factorisation, we essentially reversed this process. We started with ab + ac and identified 'a' (the GCF) to rewrite the expression as a(b + c).
Advanced Applications and Extensions
While the factorisation of 6x + 4 might seem simple, the underlying principles extend to much more complex algebraic expressions. Understanding this basic factorisation lays the groundwork for tackling more challenging problems involving:
-
Factoring quadratics: Quadratic expressions (expressions of the form ax² + bx + c) require more sophisticated techniques, but the concept of finding common factors remains fundamental. Often, you'll need to apply techniques like factoring by grouping or using the quadratic formula to find the factors.
-
Factoring polynomials of higher degree: Polynomials with higher powers of x (like x³, x⁴, etc.) can also be factored, often using similar strategies involving GCF and other advanced techniques.
-
Solving equations: Factorisation is a crucial tool for solving equations. By factoring an expression and setting each factor equal to zero, you can find the solutions (roots) of the equation. For example, if you have the equation 6x + 4 = 0, you can factor it to 2(3x + 2) = 0 and then solve for x by setting each factor equal to zero. This leads to x = -2/3.
-
Simplifying expressions: Factoring can simplify complex algebraic expressions, making them easier to work with and manipulate. This simplification is especially useful when dealing with fractions or other complex mathematical operations.
Beyond the Basics: Exploring Different Approaches
While the GCF method is the most straightforward approach for 6x + 4, it's beneficial to understand that other techniques, though not always necessary in this specific case, can be applied to different expressions:
-
Factoring by Grouping: This method is particularly useful for expressions with four or more terms. You group terms with common factors and then factor out the GCF from each group.
-
Difference of Squares: Expressions in the form a² - b² can be factored as (a + b)(a - b).
-
Perfect Square Trinomials: Expressions in the form a² + 2ab + b² or a² - 2ab + b² can be factored as (a + b)² or (a - b)², respectively.
Frequently Asked Questions (FAQ)
Q1: What if the expression had a common variable?
A1: If the terms shared a common variable, you would include that variable in the GCF. For example, if the expression was 6x² + 4x, the GCF would be 2x, leading to the factored form 2x(3x + 2).
Q2: Is there only one correct way to factor an expression?
A2: Generally, there's only one fully factored form of an expression, although it might appear slightly different depending on the order of the factors. For instance, 2(3x + 2) and (3x + 2)2 are equivalent factored forms.
Q3: What happens if there's no common factor?
A3: If there's no common factor between the terms, the expression is considered to be already in its simplest form and cannot be factored further using basic methods. However, more advanced techniques might still be applicable depending on the complexity of the expression.
Q4: Why is factoring important in higher-level mathematics?
A4: Factoring is a cornerstone skill in algebra and beyond. It's crucial for solving polynomial equations, simplifying rational expressions (fractions with polynomials), and understanding concepts like roots, zeros, and the behavior of functions. It's a building block for calculus and other advanced mathematical disciplines.
Conclusion
Factorising the expression 6x + 4, while seemingly straightforward, provides a foundational understanding of a crucial algebraic skill. Mastering this concept unlocks the ability to tackle more complex factorisation problems and forms the bedrock for success in higher-level mathematics. By understanding the underlying principles of the distributive property and applying systematic steps, you can confidently approach and solve a wide range of algebraic problems. Remember to practice regularly; the more you practice, the more intuitive and efficient your factorisation skills will become. So, continue to explore, practice, and enjoy the elegance and power of algebraic manipulation!
Latest Posts
Latest Posts
-
Katelyn Ohashi Olympics
Sep 14, 2025
-
58 2kg In Stone
Sep 14, 2025
-
70ml In Grams
Sep 14, 2025
-
1 88cm In Feet
Sep 14, 2025
-
Twister Game Mat
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6x 4 Factorise . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.