60000 / 12
stanleys
Sep 13, 2025 · 5 min read
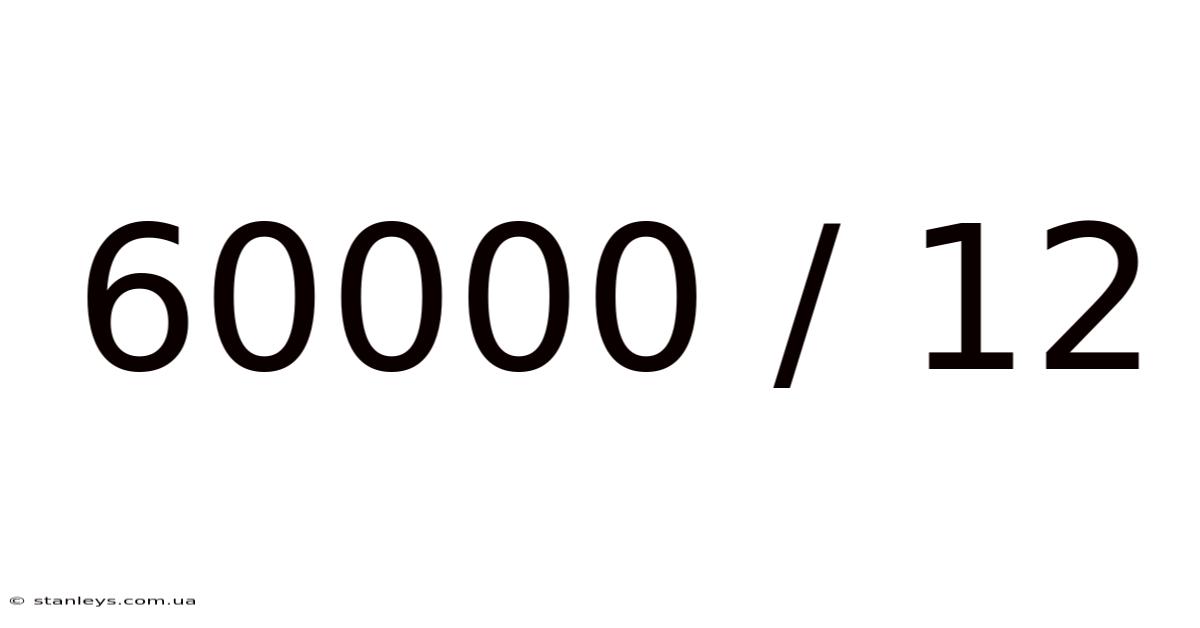
Table of Contents
Decoding 60000 / 12: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 60000 divided by 12, delving beyond the immediate answer to uncover the underlying mathematical principles and real-world applications. We'll examine different methods for solving this division problem, discuss its significance in various fields, and address frequently asked questions to provide a comprehensive understanding of this fundamental arithmetic operation. Understanding division, even in a simple example like this, lays the groundwork for more complex mathematical concepts and problem-solving skills.
Understanding the Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. In the expression 60000 / 12, we're asking: "How many times does 12 fit into 60000?" The number 60000 is the dividend, the number being divided, and 12 is the divisor, the number we're dividing by. The result of the division is the quotient.
Methods for Solving 60000 / 12
Several methods can be used to calculate 60000 / 12. Let's explore a few:
-
Long Division: This classic method involves a step-by-step process of dividing the dividend by the divisor. While it can seem tedious for larger numbers, it reinforces understanding of the division process.
5000 --------- 12 | 60000 -60 00 0 00 0 00 0 -
Mental Math: With practice, you can perform this division mentally. Recognizing that 60 divided by 12 equals 5, you can then add the remaining zeros to get 5000. This method relies on familiarity with multiplication tables and number properties.
-
Calculator: The simplest approach for larger numbers is using a calculator. This method provides an immediate result, but it's crucial to understand the underlying process.
-
Factoring: We can break down the problem by factoring. Since 60000 = 6 x 10000 and 12 = 3 x 4, we can simplify the division as follows: (6 x 10000) / (3 x 4) = (6/3) x (10000/4) = 2 x 2500 = 5000. This method highlights the flexibility in manipulating numbers to simplify calculations.
The Answer and its Significance
Regardless of the method used, the answer to 60000 / 12 is 5000. This seemingly simple result has implications across many areas:
-
Financial Calculations: Imagine dividing a $60,000 annual salary into 12 monthly payments. The result, $5000, represents the monthly salary. This is a fundamental calculation in personal finance and budgeting.
-
Unit Conversions: Consider converting 60,000 centimeters to meters. Since there are 100 centimeters in a meter, we divide 60,000 by 100 (a multiple of 12), and then further divide by 12. This highlights the interconnectedness of different measurement systems and the importance of conversion in various scientific and engineering applications.
-
Data Analysis: In statistical analysis, you might need to divide a total count of 60,000 data points into 12 groups for analysis. The quotient, 5000, would indicate the number of data points in each group. This is a fundamental aspect of data organization and processing.
-
Resource Allocation: If you have 60,000 units of a resource and need to distribute them equally among 12 teams, each team would receive 5000 units. This type of calculation is vital in project management, logistics, and supply chain operations.
Real-World Applications: Expanding the Scope
The principles demonstrated in 60000 / 12 extend far beyond simple arithmetic. Here are some more complex real-world applications:
-
Engineering and Construction: Calculating material requirements, determining the number of workers needed for a project, or estimating the cost per unit of production all involve division. A construction project might require 60,000 bricks and be divided into 12 stages; hence, 5000 bricks are needed for each stage.
-
Manufacturing and Production: Production lines often deal with large numbers. If a factory produces 60,000 units in 12 hours, the hourly production rate is 5000 units. This information is essential for production planning and efficiency improvements.
-
Economics and Finance: Analyzing economic data, calculating interest rates, or determining per-share earnings frequently involves division. For instance, determining the average daily return of an investment over a year requires dividing the total return by 365 days.
-
Scientific Research: In experimental sciences, division is used extensively. For example, calculating the average of a set of experimental results or determining the concentration of a solution involves this fundamental operation.
Expanding Mathematical Understanding: Beyond the Basics
While seemingly simple, 60000 / 12 provides a foundation for more advanced mathematical concepts:
-
Fractions and Ratios: The division problem can be expressed as a fraction (60000/12), which simplifies to a ratio of 5000:1. Understanding this relationship is vital in understanding proportions and scaling.
-
Algebra: More complex problems might involve solving for an unknown variable within a division equation. For example, x / 12 = 5000. Solving for x involves multiplication.
-
Calculus: Differential and integral calculus involve concepts of infinitesimally small changes and sums, which build upon the fundamental understanding of division.
Frequently Asked Questions (FAQ)
Q: What if the dividend isn't perfectly divisible by the divisor?
A: If the divisor doesn't divide the dividend evenly, the result will have a remainder. For instance, if we were to divide 60007 by 12, the quotient would be 5000 with a remainder of 7. This remainder can be expressed as a fraction (7/12) or a decimal (0.5833).
Q: Are there any shortcuts for division problems involving zeros?
A: Yes, when dividing by multiples of 10 (like 10, 100, 1000), you can simply move the decimal point to the left by the same number of places as the number of zeros in the divisor.
Q: How can I improve my division skills?
A: Consistent practice is key. Start with simpler problems and gradually increase the difficulty. Use different methods (long division, mental math, calculator) to develop a comprehensive understanding. Focus on understanding the underlying concepts rather than just memorizing procedures.
Conclusion: The Power of Simple Division
The seemingly simple calculation of 60000 / 12 offers a gateway to a deeper appreciation of division and its vast applications. From personal finance to complex scientific research, this fundamental arithmetic operation underpins countless calculations and processes. By mastering this seemingly basic skill, you build a foundation for more advanced mathematical understanding and problem-solving capabilities across various fields. Remember, the power of mathematics lies in its ability to dissect complex problems into smaller, manageable parts – just like dividing 60000 by 12. Understanding the "why" behind the "how" unlocks a world of possibilities.
Latest Posts
Latest Posts
-
127lbs In Kg
Sep 13, 2025
-
175 To Kg
Sep 13, 2025
-
6 7kg In Lbs
Sep 13, 2025
-
75 Of 400
Sep 13, 2025
-
5 5cm To Mm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 60000 / 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.