60 Of 280
stanleys
Sep 25, 2025 · 6 min read
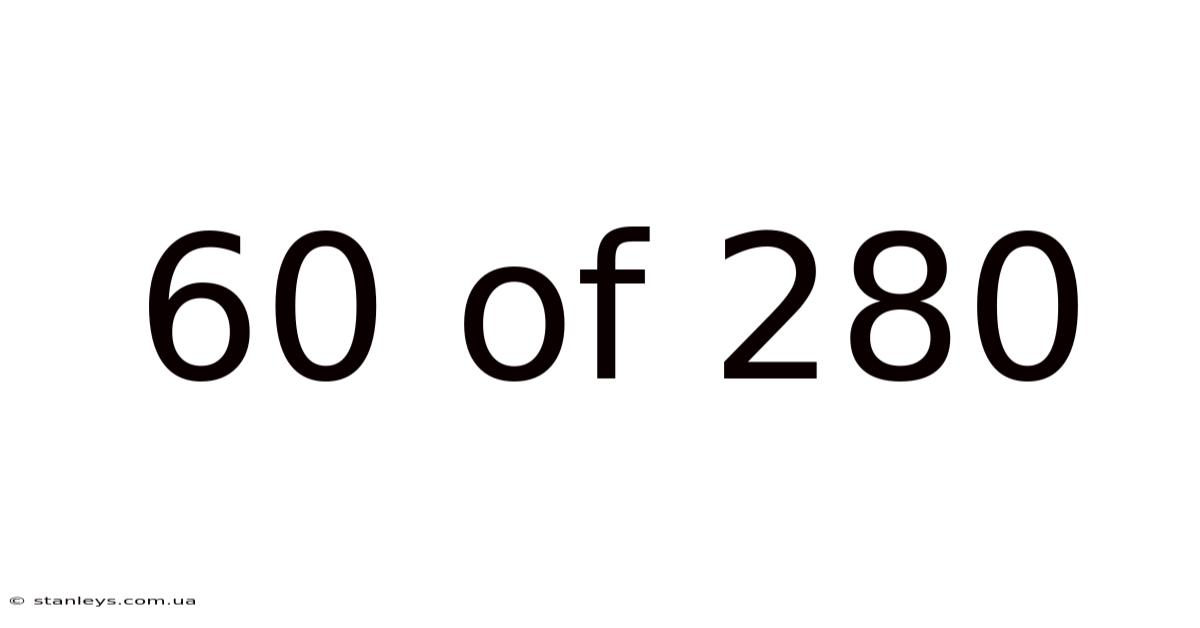
Table of Contents
Decoding the Fraction: Understanding 60/280 and its Implications
This article delves into the seemingly simple fraction 60/280, exploring its various interpretations, simplifications, and applications across different fields. We'll move beyond a simple numerical answer to understand the underlying concepts and how this fraction can be used to represent proportions, ratios, and percentages in real-world scenarios. Understanding fractions like 60/280 is crucial for basic arithmetic, higher-level mathematics, and even everyday problem-solving.
Introduction: The Significance of Fractions
Fractions are fundamental building blocks of mathematics. They represent parts of a whole, expressing a relationship between a numerator (the top number) and a denominator (the bottom number). The fraction 60/280 indicates that we have 60 parts out of a possible 280 parts. While seemingly straightforward, this fraction offers numerous avenues for exploration and application.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before exploring the applications of 60/280, it's essential to simplify the fraction to its lowest terms. This makes the fraction easier to understand and work with. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by this GCD.
Let's find the GCD of 60 and 280. We can use the prime factorization method:
- Prime factorization of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
- Prime factorization of 280: 2 x 2 x 2 x 5 x 7 = 2³ x 5 x 7
The common factors are 2 and 5. Therefore, the GCD is 2 x 5 = 10.
Now, we divide both the numerator and denominator by 10:
60 ÷ 10 = 6 280 ÷ 10 = 28
Therefore, the simplified fraction is 6/28.
We can further simplify this fraction by noticing that both 6 and 28 are divisible by 2:
6 ÷ 2 = 3 28 ÷ 2 = 14
So, the simplest form of 60/280 is 3/14.
Representing the Fraction as a Decimal and Percentage
The simplified fraction 3/14 can be easily converted into a decimal and a percentage.
To convert to a decimal, we divide the numerator by the denominator:
3 ÷ 14 ≈ 0.2143
To convert the decimal to a percentage, we multiply by 100:
0.2143 x 100 ≈ 21.43%
Therefore, 60/280 represents approximately 21.43%.
Real-World Applications of the Fraction 60/280 (or 3/14)
The fraction 60/280, or its simplified form 3/14, can be applied in various real-world contexts:
-
Proportions: Imagine a survey where 60 out of 280 respondents answered "yes" to a particular question. The fraction 3/14 represents the proportion of "yes" responses. This proportion can be used to draw inferences about the population surveyed.
-
Ratios: Suppose a recipe calls for 60 grams of sugar and 280 grams of flour. The ratio of sugar to flour is 60:280, which simplifies to 3:14. This ratio helps maintain the correct proportions when scaling the recipe up or down.
-
Probabilities: If an event has a probability of 60 out of 280, the probability simplifies to 3/14. This can be useful in various fields like gambling, statistics, and risk assessment.
-
Geometry: The fraction could represent the ratio of lengths, areas, or volumes in geometric figures. For instance, it could describe the relationship between the sides of a rectangle or the segments of a line.
-
Data Analysis: In data analysis, 60/280 might represent a portion of a dataset or a particular outcome within a sample. Understanding this fraction is crucial for interpreting data accurately.
Understanding the Concept of Ratios and Proportions
The fraction 60/280 intrinsically relates to the concepts of ratios and proportions. A ratio compares two or more quantities, while a proportion states that two ratios are equal. In the case of 60/280, we can express it as a ratio of 60:280 or the simplified ratio 3:14. A proportion might involve comparing this ratio to another, for example, determining if the ratio of apples to oranges in one basket is equivalent to the ratio of apples to oranges in another.
Solving Problems Involving 60/280
Let's explore a few example problems involving the fraction 60/280:
Problem 1: A school has 280 students. 60 of them participate in sports. What percentage of students participate in sports?
Solution: This problem directly uses the fraction 60/280. We've already established that this simplifies to approximately 21.43%. Therefore, approximately 21.43% of the students participate in sports.
Problem 2: If a recipe requires 60 grams of sugar for 280 grams of flour, how much sugar is needed for 700 grams of flour?
Solution: We can set up a proportion:
60/280 = x/700
Cross-multiplying and solving for x:
280x = 60 * 700 280x = 42000 x = 42000/280 x = 150
Therefore, 150 grams of sugar are needed for 700 grams of flour.
Problem 3: A bag contains 280 marbles. 60 are red. If you randomly select a marble, what is the probability that it will be red?
Solution: The probability of selecting a red marble is 60/280, which simplifies to 3/14. This means there's a 3 out of 14 chance of selecting a red marble.
Further Exploration: Working with More Complex Fractions
Understanding 60/280 provides a solid foundation for working with more complex fractions and ratios. The principles of simplification, decimal conversion, percentage calculation, and application to real-world problems remain consistent. As you encounter more complex fractions, remember to apply these fundamental concepts consistently.
Frequently Asked Questions (FAQ)
Q1: Can 60/280 be simplified further after reaching 3/14?
A1: No, 3/14 is the simplest form of the fraction because 3 and 14 share no common divisors other than 1.
Q2: What if the fraction was 280/60 instead of 60/280?
A2: The fraction 280/60 would simplify to 14/3, which is an improper fraction (where the numerator is larger than the denominator). This improper fraction can be expressed as a mixed number (4 and 2/3) or as a decimal (approximately 4.67). The interpretation would be different, representing a quantity larger than one whole.
Q3: How do I convert a fraction to a percentage quickly?
A3: To quickly convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100.
Q4: What are some other methods for finding the GCD?
A4: Besides prime factorization, the Euclidean algorithm is another efficient method for finding the greatest common divisor of two numbers.
Conclusion: The Power of Understanding Fractions
The seemingly simple fraction 60/280 offers a rich opportunity to explore fundamental mathematical concepts. By simplifying the fraction to its lowest terms (3/14), converting it to a decimal and a percentage, and understanding its applications in ratios, proportions, and probabilities, we gain a deeper appreciation of its significance. Mastering the manipulation and interpretation of fractions like 60/280 is crucial not only for academic success but also for navigating various aspects of everyday life. The ability to understand and apply these concepts empowers you to solve problems effectively and interpret data accurately across numerous disciplines. Remember that practice is key; the more you work with fractions, the more comfortable and confident you will become in your understanding and application.
Latest Posts
Related Post
Thank you for visiting our website which covers about 60 Of 280 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.